
Tóm tắt: Đồ thị histogram là công cụ trực quan quan trọng trong thực hành kinh tế lượng, cho phép khám phá và hiển thị phân phối tần suất của dữ liệu liên tục. Bài viết hướng dẫn chi tiết cách xây dựng, phân tích và diễn giải histogram để kiểm tra phân phối chuẩn, phát hiện điểm dị biệt, đánh giá độ lệch và độ nhọn. Nội dung bao gồm nguyên tắc chọn bins phù hợp, so sánh với bar chart, ứng dụng trong nghiên cứu kinh tế Việt Nam và code thực hành trên SPSS, Stata, R, Python.
Giới thiệu
Nội dung chính
- Giới thiệu
- Histogram là gì?
- Ví dụ thực tế từ kinh tế Việt Nam
- Xây dựng đồ thị histogram cho biến liên tục
- Chọn độ rộng bins hợp lý
- Nguyên tắc diện tích trong histogram
- So sánh histogram và bar chart
- Hướng dẫn thực hành chi tiết
- Phân tích và diễn giải histogram
- Ứng dụng trong nghiên cứu kinh tế Việt Nam
- Lưu ý và cảnh báo quan trọng
- Tổng kết
- Phụ lục: Code thực hành trên các phần mềm
- Tài liệu tham khảo
Trong thực hành kinh tế lượng, việc hiểu rõ phân phối của dữ liệu là bước đầu tiên và quan trọng nhất trước khi thực hiện bất kỳ phân tích nào. Trực quan hóa dữ liệu thông qua đồ thị histogram giúp các nhà nghiên cứu kinh tế nhanh chóng nhận biết những đặc điểm quan trọng của biến số.
Ví dụ trong nghiên cứu kinh tế Việt Nam, khi phân tích phân phối thu nhập hộ gia đình, điểm thi đại học, hoặc giá cả hàng hóa, histogram giúp chúng ta hiểu rõ:
- Dữ liệu có phân phối chuẩn hay không?
- Có tồn tại những giá trị bất thường (outliers)?
- Phân phối có lệch trái hay lệch phải?
- Mức độ tập trung của dữ liệu quanh giá trị trung tâm
Histogram là gì?
Histogram là một dạng đồ thị cho phép các bạn khám phá và hiển thị phân phối tần suất của một tập dữ liệu liên tục. Nó cho phép chúng ta kiểm tra dạng phân phối (chẳng hạn, phân phối chuẩn), điểm dị biệt, độ lệch, độ nhọn của tập dữ liệu.
Một đồ thị histogram điển hình có dạng như sau:

Ví dụ thực tế từ kinh tế Việt Nam
Để minh họa cách xây dựng histogram, chúng ta sử dụng ví dụ về độ tuổi của lao động trong một cuộc khảo sát thị trường lao động tại Việt Nam. Giả sử chúng ta có dữ liệu về tuổi của 20 lao động như sau:
36 25 38 46 55 68 72 55 36 38
67 45 22 48 91 46 52 61 58 55
Dữ liệu này phản ánh cấu trúc tuổi đa dạng của lực lượng lao động Việt Nam, từ lao động trẻ (22 tuổi) đến lao động cao tuổi (91 tuổi). Việc phân tích phân phối độ tuổi này giúp:
- Đánh giá cơ cấu lao động theo độ tuổi
- Xác định nhóm tuổi chính trong mẫu khảo sát
- Phát hiện những lao động có độ tuổi bất thường
- Đưa ra khuyến nghị chính sách lao động phù hợp
Xây dựng đồ thị histogram cho biến liên tục
Để xây dựng đồ thị histogram từ một biến liên tục trong thực hành kinh tế lượng, việc đầu tiên là cần phải chuyển dữ liệu sang dạng khoảng (interval), mà chúng ta gọi là các bins. Trong ví dụ trên, biến tuổi được chia thành các bins, mỗi bin đại diện cho một nhóm tuổi (cách nhau 10 tuổi và bắt đầu từ 20).
Phân chia dữ liệu thành bins
Mỗi bin bao gồm số các quan sát thỏa mãn điều kiện của bin xuất hiện trong tập dữ liệu. Thông tin của mẫu dữ liệu trên được thể hiện dưới dạng các bins như sau:
Bin Tần số Các quan sát (tuổi)
20-30 2 25, 22
30-40 4 36, 38, 36, 38
40-50 4 46, 45, 48, 46
50-60 5 55, 55, 52, 58, 55
60-70 3 68, 67, 61
70-80 1 72
80-90 0 –
90-100 1 91
Công thức tính bins tối ưu
Trong thực hành kinh tế lượng, có nhiều quy tắc để xác định số bins phù hợp:
- Sturges’ rule: $k = 1 + \log_2(n)$ trong đó $k$ là số thanh, $n$ là số quan sát
- Scott’s rule: Bề rộng thanh (Bin width) $= \frac{3.5 \times s}{n^{1/3}}$ trong đó $s$ là độ lệch chuẩn
- Freedman-Diaconis rule: Bề rộng thanh (Bin width) $= \frac{2 \times IQR}{n^{1/3}}$ trong đó $IQR$ là khoảng tứ phân vị
Với dữ liệu 20 quan sát trong ví dụ, theo quy tắc Sturges (Sturges’ rule): $k = 1 + \log_2(20) = 1 + 4.32 \approx 5$ thanh.
Chọn độ rộng bins hợp lý
Việc chọn độ rộng bins phù hợp là yếu tố quan trọng quyết định chất lượng histogram trong thực hành kinh tế lượng. Không có câu trả lời tuyệt đối đúng hay sai về độ rộng của các bins, nhưng có một vài quy tắc kinh nghiệm quan trọng.
Chúng ta cần đảm bảo rằng các thanh không được quá nhỏ hoặc quá lớn như minh họa sau:
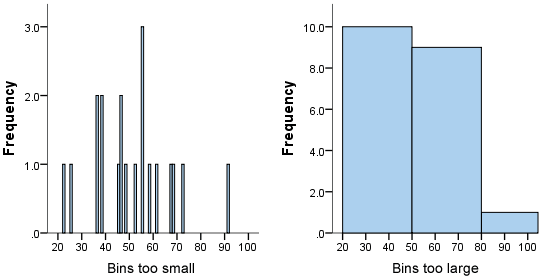
Bins quá nhỏ
Ở đồ thị histogram bên trái, độ rộng của thanh quá nhỏ dẫn đến:
- Hiển thị quá nhiều chi tiết không cần thiết
- Không thể hiện được xu hướng tổng thể của phân phối
- Gây nhiễu thông tin, khó đọc hiểu
- Không phù hợp cho báo cáo và trình bày
Bins quá lớn
Ở đồ thị histogram bên phải, các thanh quá lớn gây ra:
- Mất thông tin quan trọng về phân phối
- Không phát hiện được các đặc điểm như phân phối nhị thức (bimodal distribution)
- Che giấu sự tồn tại của các ngoại lai
- Đơn giản hóa quá mức, không phản ánh thực tế

Nguyên tắc diện tích trong histogram
Một điểm quan trọng trong thực hành kinh tế lượng là hiểu rằng histogram dựa vào diện tích chứ không phải chiều cao của các thanh. Điều này có ý nghĩa thực tiễn quan trọng:
Công thức tính tần suất
Đối với đồ thị histogram, diện tích của bin thể hiện tần suất xuất hiện của mỗi bin:
Tần suất = Chiều cao × Chiều rộng của bin
Điều này có nghĩa rằng:
- Chiều cao của thanh không trực tiếp thể hiện tần suất
- Khi bins có độ rộng khác nhau, cần chú ý đến diện tích
- Density histogram sử dụng mật độ thay vì tần suất thuần túy
- Tổng diện tích của tất cả bins bằng một trong density histogram
Ứng dụng trong phân tích kinh tế
Trong nghiên cứu kinh tế Việt Nam, nguyên tắc diện tích này đặc biệt quan trọng khi:
- So sánh phân phối thu nhập giữa các vùng miền có cỡ mẫu khác nhau
- Phân tích phân phối giá cả với các khoảng giá không đều
- Nghiên cứu phân phối độ tuổi lao động theo ngành nghề
- Đánh giá phân phối điểm thi với thang điểm khác nhau
So sánh histogram và bar chart
Một điểm quan trọng trong thực hành kinh tế lượng là phân biệt rõ ràng giữa histogram và bar chart (biểu đồ cột):
So sánh histogram và bar chart
Không giống đồ thị thanh (bar chart), đồ thị histogram không có các khoảng trống (gaps) giữa các thanh (mặc dù một vài thanh có thể có khoảng trống vì tần suất xuất hiện bằng 0). Điều này bởi vì đồ thị histogram đặc trưng cho dữ liệu liên tục. Ngoài ra, sự khác biệt chủ yếu giữa đồ thị histogram và đồ thị thanh (bar) là đồ thị histogram chỉ sử dụng để hiển thị tần số xuất hiện của các quan sát trong tập dữ liệu liên tục được chia thành các khoảng (bins). Ngược lại, các đồ thị dạng thanh có thể được sử dụng cho các tập dữ liệu thuộc kiểu khác như thứ tự (ordinal) và định danh (nominal).
Bảng so sánh chi tiết
| Đặc điểm | Histogram | Bar Chart |
|---|---|---|
| Loại dữ liệu | Dữ liệu liên tục (continuous) | Dữ liệu phân loại (categorical) |
| Khoảng cách giữa các cột | Không có khoảng trống | Có khoảng trống |
| Ý nghĩa trục X | Khoảng giá trị (bins) | Danh mục riêng biệt |
| Ý nghĩa diện tích | Tần suất xuất hiện | Không có ý nghĩa đặc biệt |
| Ứng dụng trong kinh tế | Thu nhập, giá cả, tuổi tác | Ngành nghề, vùng miền, giới tính |
Hướng dẫn thực hành chi tiết
Tạo histogram trong SPSS
Để tạo histogram trong SPSS cho thực hành kinh tế lượng:
- Chọn Graphs → Chart Builder
- Kéo biểu tượng Histogram từ Choose from vào canvas
- Kéo biến liên tục vào trục X-Axis
- Nhấn OK để tạo đồ thị
Tùy chỉnh histogram chuyên nghiệp
Để tạo histogram chất lượng cao phục vụ nghiên cứu:
- Điều chỉnh số bins: Double-click vào histogram, chọn Properties, điều chỉnh Number of bins
- Thêm đường phân phối chuẩn: Chọn Display normal curve để so sánh với phân phối chuẩn
- Tùy chỉnh màu sắc: Chọn màu phù hợp với tiêu chuẩn xuất bản khoa học
- Thêm title và labels: Đảm bảo đồ thị có tiêu đề và nhãn trục rõ ràng
Phân tích và diễn giải histogram
Khi phân tích histogram trong thực hành kinh tế lượng, cần chú ý những yếu tố sau:
1. Hình dạng phân phối
- Phân phối chuẩn: Hình chuông đối xứng quanh trung bình
- Lệch phải (right-skewed): Đuôi dài về phía phải, thường gặp trong phân phối thu nhập
- Lệch trái (left-skewed): Đuôi dài về phía trái, ít gặp trong dữ liệu kinh tế
- Bimodal: Hai đỉnh, thể hiện hai nhóm phân biệt trong dữ liệu
2. Phát hiện outliers
Histogram giúp phát hiện các giá trị bất thường:
3. Đánh giá tính chuẩn
Để kiểm tra tính chuẩn của phân phối:
- So sánh với đường cong phân phối chuẩn overlay
- Kiểm tra tính đối xứng quanh giá trị trung bình
- Đánh giá độ nhọn (kurtosis) so với phân phối chuẩn
- Sử dụng thêm Q-Q plot để xác nhận
Ứng dụng trong nghiên cứu kinh tế Việt Nam
Histogram có nhiều ứng dụng quan trọng trong nghiên cứu kinh tế Việt Nam:
1. Phân tích phân phối thu nhập
Khi nghiên cứu bất bình đẳng thu nhập tại Việt Nam:
- Histogram thu nhập thường có dạng lệch phải với đuôi dài
- Phần lớn dân số có thu nhập thấp đến trung bình
- Một số ít có thu nhập rất cao (top 1%, 5%)
- Giúp xác định các mức thu nhập phân vị quan trọng
2. Nghiên cứu giá cả hàng hóa
Trong phân tích thị trường hàng hóa:
- Histogram giá giúp xác định mức giá phổ biến
- Phát hiện các mức giá bất thường (có thể do lỗi dữ liệu)
- Đánh giá sự phân tán giá trên thị trường
- So sánh phân phối giá giữa các vùng miền
3. Phân tích điểm thi và giáo dục
Trong nghiên cứu hiệu quả giáo dục:
- Histogram điểm thi cho thấy chất lượng giáo dục
- Phân phối chuẩn là lý tưởng cho hầu hết bài thi
- Phân phối lệch có thể báo hiệu vấn đề về độ khó đề thi
- Giúp thiết lập thang điểm và chuẩn đánh giá
Lưu ý và cảnh báo quan trọng
Khi sử dụng histogram trong thực hành kinh tế lượng, cần lưu ý:
Những lỗi thường gặp
- Chọn số bins không phù hợp: Quá ít hoặc quá nhiều bins làm méo mó thông tin
- Bỏ qua outliers: Không xem xét ảnh hưởng của các giá trị bất thường
- Hiểu sai ý nghĩa chiều cao: Nhầm lẫn giữa frequency và density
- So sánh không đồng nhất: So sánh các histogram có thang đo (scale) khác nhau
Best practices
- Luôn báo cáo phương pháp chọn bins được sử dụng
- Kết hợp histogram với các thống kê mô tả (mean, median, SD)
- Sử dụng màu sắc và format nhất quán trong cùng một báo cáo
- Thêm các đường tham chiếu quan trọng (mean, median, percentiles)
Giới hạn của histogram
- Histogram chỉ hiển thị phân phối của một biến (univariate)
- Không thể hiện mối quan hệ giữa các biến
- Kết quả có thể thay đổi đáng kể tùy theo cách chọn bins
- Với dữ liệu ít, histogram có thể gây hiểu lầm
Tổng kết
Đồ thị histogram là công cụ không thể thiếu trong thực hành kinh tế lượng, giúp các nhà nghiên cứu hiểu rõ đặc điểm phân phối của dữ liệu trước khi tiến hành các phân tích phức tạp hơn. Việc thành thạo cách xây dựng, tùy chỉnh và diễn giải histogram sẽ nâng cao đáng kể chất lượng nghiên cứu kinh tế.
Qua các ví dụ thực tế từ kinh tế Việt Nam, chúng ta đã thấy tầm quan trọng của histogram trong:
- Phát hiện các đặc điểm quan trọng của phân phối dữ liệu
- Kiểm tra giả định phân phối chuẩn cho các kiểm định thống kê
- Phát hiện và xử lý các giá trị bất thường
- Trình bày kết quả nghiên cứu một cách trực quan và thuyết phục
Điều quan trọng là phải hiểu rõ nguyên tắc cơ bản về bins, diện tích, và sự khác biệt với bar chart để áp dụng đúng cách trong từng bối cảnh nghiên cứu cụ thể.
Key Points:
- Histogram là công cụ trực quan hóa dữ liệu liên tục thông qua phân chia thành bins
- Việc chọn số bins và độ rộng bins ảnh hưởng quan trọng đến chất lượng histogram
- Diện tích (không phải chiều cao) của các cột thể hiện tần suất trong histogram
- Histogram khác biệt cơ bản với bar chart ở chỗ không có khoảng trống giữa các cột
- Histogram giúp kiểm tra tính chuẩn, phát hiện các ngoại lai và đánh giá độ lệch của phân phối
- Ứng dụng rộng rãi trong nghiên cứu thu nhập, giá cả, điểm thi và các biến kinh tế khác
- Cần kết hợp với các thống kê mô tả để có cái nhìn toàn diện về dữ liệu
Phụ lục: Code thực hành trên các phần mềm
SPSS Syntax
SPSS Syntax (.sps)
* Tạo histogram trong SPSS bằng Syntax
* Tác giả: Thực hành kinh tế lượng
* Ví dụ: Phân tích phân phối tuổi lao động
* Nhập dữ liệu mẫu về tuổi
DATA LIST FREE / age.
BEGIN DATA
36 25 38 46 55 68 72 55 36 38
67 45 22 48 91 46 52 61 58 55
END DATA.
* Tạo histogram cơ bản
GRAPH /HISTOGRAM=age.
* Tạo histogram với đường cong phân phối chuẩn
GRAPH /HISTOGRAM(NORMAL)=age.
* Tạo histogram với số bins tùy chỉnh
GRAPH /HISTOGRAM(NORMAL)=age
/HISTOGRAM FORMAT=INTERVAL WIDTH(AUTO) SCALE(FREQ)
/TITLE='Phân phối tuổi lao động Việt Nam'.
* Thống kê mô tả kèm theo
FREQUENCIES VARIABLES=age
/HISTOGRAM NORMAL
/STATISTICS=STDDEV VARIANCE RANGE MINIMUM MAXIMUM MEAN MEDIAN MODE SKEWNESS SESKEW KURTOSIS SEKURT.
* Tạo multiple histograms theo nhóm
* (Giả sử có biến region: 1=Bắc, 2=Trung, 3=Nam)
GRAPH /HISTOGRAM=age
/PANEL ROWVAR=region ROWOP=CROSS.
Stata
Code Stata (.do)
// Tạo histogram trong Stata
// Tác giả: Thực hành kinh tế lượng
// Ví dụ: Phân tích phân phối tuổi lao động
* Xóa dữ liệu hiện tại
clear
* Nhập dữ liệu mẫu về tuổi
input age
36
25
38
46
55
68
72
55
36
38
67
45
22
48
91
46
52
61
58
55
end
* Tạo histogram cơ bản
histogram age, title("Phân phối tuổi lao động") ///
xtitle("Tuổi") ytitle("Mật độ")
* Tạo histogram với overlay normal curve
histogram age, normal title("Phân phối tuổi với đường cong chuẩn") ///
xtitle("Tuổi") ytitle("Mật độ")
* Tùy chỉnh số bins
histogram age, bin(6) title("Histogram với 6 bins") ///
xtitle("Tuổi") ytitle("Mật độ")
* Histogram với density thay vì frequency
histogram age, density normal title("Density histogram") ///
xtitle("Tuổi") ytitle("Mật độ")
* Thống kê mô tả
summarize age, detail
* Kiểm định tính chuẩn
swilk age
sktest age
* Tạo histogram theo nhóm (ví dụ theo region)
* generate region = ceil(_n/7) // Tạo biến region giả định
* histogram age, by(region) title("Phân phối tuổi theo vùng")
* Lưu histogram
graph save "histogram_age.gph", replace
graph export "histogram_age.png", replace
R
Code R (.R)
# Tạo histogram trong R
# Tác giả: Thực hành kinh tế lượng
# Ví dụ: Phân tích phân phối tuổi lao động
# Cài đặt và load các package cần thiết
if (!require(ggplot2)) install.packages("ggplot2")
if (!require(dplyr)) install.packages("dplyr")
if (!require(nortest)) install.packages("nortest")
library(ggplot2)
library(dplyr)
library(nortest)
# Tạo dữ liệu mẫu về tuổi
age <- c(36, 25, 38, 46, 55, 68, 72, 55, 36, 38,
67, 45, 22, 48, 91, 46, 52, 61, 58, 55)
# Tạo data frame
data <- data.frame(age = age)
# Histogram cơ bản với base R
hist(age,
main = "Phân phối tuổi lao động Việt Nam",
xlab = "Tuổi",
ylab = "Tần số",
col = "lightblue",
border = "black")
# Histogram với đường cong normal
hist(age,
main = "Phân phối tuổi với đường cong chuẩn",
xlab = "Tuổi",
ylab = "Tần số",
col = "lightblue",
border = "black",
prob = TRUE) # Hiển thị density thay vì frequency
# Thêm đường cong normal
curve(dnorm(x, mean = mean(age), sd = sd(age)),
add = TRUE, col = "red", lwd = 2)
# Histogram với ggplot2 (chuyên nghiệp hơn)
p1 <- ggplot(data, aes(x = age)) +
geom_histogram(aes(y = ..density..),
binwidth = 10,
fill = "lightblue",
color = "black",
alpha = 0.7) +
stat_function(fun = dnorm,
args = list(mean = mean(age), sd = sd(age)),
color = "red", size = 1) +
labs(title = "Phân phối tuổi lao động (ggplot2)",
x = "Tuổi",
y = "Mật độ") +
theme_minimal()
print(p1)
# Histogram với số bins khác nhau
par(mfrow = c(2, 2))
hist(age, breaks = 5, main = "5 bins", col = "lightblue")
hist(age, breaks = 8, main = "8 bins", col = "lightgreen")
hist(age, breaks = 15, main = "15 bins", col = "pink")
hist(age, breaks = 20, main = "20 bins", col = "lightyellow")
par(mfrow = c(1, 1))
# Thống kê mô tả
summary(age)
cat("Độ lệch chuẩn:", sd(age), "\n")
cat("Skewness:", moments::skewness(age), "\n")
cat("Kurtosis:", moments::kurtosis(age), "\n")
# Kiểm định tính chuẩn
shapiro.test(age)
lillie.test(age)
# Tạo Q-Q plot để kiểm tra tính chuẩn
qqnorm(age, main = "Q-Q Plot")
qqline(age, col = "red")
# Histogram theo nhóm (ví dụ)
# Tạo biến region giả định
data$region <- rep(c("Bắc", "Trung", "Nam"), length.out = length(age))
ggplot(data, aes(x = age)) +
geom_histogram(binwidth = 10, fill = "lightblue", alpha = 0.7) +
facet_wrap(~region) +
labs(title = "Phân phối tuổi theo vùng miền",
x = "Tuổi",
y = "Tần số") +
theme_minimal()
# Lưu đồ thị
ggsave("histogram_age.png", width = 10, height = 6)
Python
Code Python (.py)
# Tạo histogram trong Python
# Tác giả: Thực hành kinh tế lượng
# Ví dụ: Phân tích phân phối tuổi lao động
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
from scipy import stats
from scipy.stats import shapiro, normaltest
import warnings
warnings.filterwarnings('ignore')
# Thiết lập font tiếng Việt
plt.rcParams['font.family'] = 'DejaVu Sans'
# Tạo dữ liệu mẫu về tuổi
age_data = [36, 25, 38, 46, 55, 68, 72, 55, 36, 38,
67, 45, 22, 48, 91, 46, 52, 61, 58, 55]
# Tạo DataFrame
df = pd.DataFrame({'age': age_data})
# Histogram cơ bản với matplotlib
plt.figure(figsize=(10, 6))
plt.hist(age_data, bins=8, color='lightblue', edgecolor='black', alpha=0.7)
plt.title('Phân phối tuổi lao động Việt Nam', fontsize=14, fontweight='bold')
plt.xlabel('Tuổi', fontsize=12)
plt.ylabel('Tần số', fontsize=12)
plt.grid(True, alpha=0.3)
plt.show()
# Histogram với đường cong normal
plt.figure(figsize=(10, 6))
count, bins, ignored = plt.hist(age_data, bins=8, density=True,
color='lightblue', edgecolor='black', alpha=0.7)
# Thêm đường cong normal
mu, sigma = np.mean(age_data), np.std(age_data)
x = np.linspace(min(age_data), max(age_data), 100)
plt.plot(x, stats.norm.pdf(x, mu, sigma), 'r-', linewidth=2,
label=f'Normal(μ={mu:.1f}, σ={sigma:.1f})')
plt.title('Phân phối tuổi với đường cong chuẩn', fontsize=14, fontweight='bold')
plt.xlabel('Tuổi', fontsize=12)
plt.ylabel('Mật độ', fontsize=12)
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
# Histogram với seaborn (đẹp hơn)
plt.figure(figsize=(10, 6))
sns.histplot(data=df, x='age', bins=8, kde=True, stat='density')
plt.title('Phân phối tuổi với KDE (Seaborn)', fontsize=14, fontweight='bold')
plt.xlabel('Tuổi', fontsize=12)
plt.ylabel('Mật độ', fontsize=12)
plt.show()
# So sánh histogram với số bins khác nhau
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
bins_list = [5, 8, 15, 20]
colors = ['lightblue', 'lightgreen', 'pink', 'lightyellow']
for i, (bins, color) in enumerate(zip(bins_list, colors)):
ax = axes[i//2, i%2]
ax.hist(age_data, bins=bins, color=color, edgecolor='black', alpha=0.7)
ax.set_title(f'{bins} bins')
ax.set_xlabel('Tuổi')
ax.set_ylabel('Tần số')
ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# Thống kê mô tả
print("=== THỐNG KÊ MÔ TẢ ===")
print(f"Số quan sát: {len(age_data)}")
print(f"Trung bình: {np.mean(age_data):.2f}")
print(f"Trung vị: {np.median(age_data):.2f}")
print(f"Độ lệch chuẩn: {np.std(age_data, ddof=1):.2f}")
print(f"Min: {np.min(age_data)}")
print(f"Max: {np.max(age_data)}")
print(f"Skewness: {stats.skew(age_data):.3f}")
print(f"Kurtosis: {stats.kurtosis(age_data):.3f}")
# Kiểm định tính chuẩn
print("\n=== KIỂM ĐỊNH TÍNH CHUẨN ===")
# Shapiro-Wilk test
shapiro_stat, shapiro_p = shapiro(age_data)
print(f"Shapiro-Wilk test: W = {shapiro_stat:.4f}, p-value = {shapiro_p:.4f}")
# D'Agostino and Pearson's test
dagostino_stat, dagostino_p = normaltest(age_data)
print(f"D'Agostino test: χ² = {dagostino_stat:.4f}, p-value = {dagostino_p:.4f}")
if shapiro_p > 0.05:
print("Kết luận: Dữ liệu có thể có phân phối chuẩn (p > 0.05)")
else:
print("Kết luận: Dữ liệu không có phân phối chuẩn (p ≤ 0.05)")
# Q-Q plot
plt.figure(figsize=(8, 6))
stats.probplot(age_data, dist="norm", plot=plt)
plt.title('Q-Q Plot', fontsize=14, fontweight='bold')
plt.grid(True, alpha=0.3)
plt.show()
# Histogram theo nhóm (giả định có biến region)
np.random.seed(42)
regions = np.random.choice(['Bắc', 'Trung', 'Nam'], size=len(age_data))
df['region'] = regions
# Subplot theo region
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
regions_unique = df['region'].unique()
for i, region in enumerate(regions_unique):
data_region = df[df['region'] == region]['age']
axes[i].hist(data_region, bins=5, color='lightblue', edgecolor='black', alpha=0.7)
axes[i].set_title(f'Vùng {region}')
axes[i].set_xlabel('Tuổi')
axes[i].set_ylabel('Tần số')
axes[i].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# Boxplot để phát hiện outliers
plt.figure(figsize=(8, 6))
plt.boxplot(age_data, vert=True)
plt.title('Boxplot - Phát hiện outliers', fontsize=14, fontweight='bold')
plt.ylabel('Tuổi', fontsize=12)
plt.grid(True, alpha=0.3)
plt.show()
# Tính outliers bằng IQR method
Q1 = np.percentile(age_data, 25)
Q3 = np.percentile(age_data, 75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
outliers = [x for x in age_data if x < lower_bound or x > upper_bound]
print(f"\n=== PHÁT HIỆN OUTLIERS ===")
print(f"Q1: {Q1}")
print(f"Q3: {Q3}")
print(f"IQR: {IQR}")
print(f"Lower bound: {lower_bound}")
print(f"Upper bound: {upper_bound}")
print(f"Outliers: {outliers}")
# Lưu đồ thị
plt.figure(figsize=(10, 6))
plt.hist(age_data, bins=8, color='lightblue', edgecolor='black', alpha=0.7)
plt.title('Phân phối tuổi lao động Việt Nam', fontsize=14, fontweight='bold')
plt.xlabel('Tuổi', fontsize=12)
plt.ylabel('Tần số', fontsize=12)
plt.grid(True, alpha=0.3)
plt.savefig('histogram_age.png', dpi=300, bbox_inches='tight')
plt.show()
print("\nĐồ thị đã được lưu thành file 'histogram_age.png'")
Tài liệu tham khảo
- Wilkinson, L. (2005). The Grammar of Graphics. 2nd Edition. Springer-Verlag.
- Tufte, E. R. (2001). The Visual Display of Quantitative Information. 2nd Edition. Graphics Press.
- Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics. 5th Edition. SAGE Publications.
- Freedman, D., & Diaconis, P. (1981). On the histogram as a density estimator: L2 theory. Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete, 57(4), 453-476.
- Scott, D. W. (2015). Multivariate Density Estimation: Theory, Practice, and Visualization. 2nd Edition. John Wiley & Sons.
- Hoàng Trọng & Chu Nguyễn Mộng Ngọc. (2019). Phân tích dữ liệu nghiên cứu với SPSS. NXB Hồng Đức.
- Nguyễn Khánh Trung. (2020). Thực hành kinh tế lượng với phần mềm thống kê. NXB Thống kê.
- Chambers, J., Cleveland, W., Kleiner, B., & Tukey, P. (1983). Graphical Methods for Data Analysis. Wadsworth & Brooks/Cole.