Tương quan và hồi quy tuyến tính

I. GIỚI THIỆU PHÂN TÍCH TƯƠNG QUAN VÀ HỒI QUY TUYẾN TÍNH GIẢN ĐƠN

Phân tích tương quan phân tích mối quan hệ giữa 2 biến. Giá trị của hệ số tương quan cho biết mức độ liên hệ mạnh giữa 2 biến. Yêu cầu của phương pháp là mẫu được chọn theo phương pháp chọn mẫu ngẫu nhiên. Trong nhiều trường hợp, phân tích tương quan có nhiều điểm tương đồng với hồi quy tuyến tính giản đơn. Chẳng hạn như cả hai đều cho thấy mối liên hệ giữa 2 biến. Hệ số ước lượng, cũng như hệ số tương quan giữa 2 biến càng lớn thì mức độ liên hệ giữa 2 biến càng chặt. Cả 2 đều cho giá trị p-value giống nhau trong các kiểm định giả thuyết.

Tuy nhiên, chúng ta không thể đồng nhất việc thực hiện phân tích tương quan và hồi quy tuyến tính giản đơn. Mỗi phương pháp đều có những đặc điểm riêng và phạm vi ứng dụng cụ thể. Bài viết sau sẽ phân biệt 2 phương pháp (tương quan và hồi quy tuyến tính giản đơn) này.

II. PHƯƠNG PHÁP PHÂN TÍCH

Phân tích tương quan 2 biến từ mẫu ngẫu nhiên từ tổng thể, trong khi hồi quy bạn chọn giá trị biến độc lập X.

Chẳng hạn, bạn muốn biết mối liên hệ giữa độ dài bàn chân với chiều cao của con người. Bạn tiến hành đo lường độ dài bàn chân và chiều cao của bất kì người nào và tính được hệ số \({r^2}\) bằng 0.72. Đây chính là hệ số tương quan bởi vì nó đo lường giá trị 2 biến từ mẫu ngẫu nhiên trong tổng thể. Bạn có thể sử dụng giá trị \({r^2}\) giữa độ dài bàn chân và chiều cao để so sánh với các mối liên hệ khác, ví dụ như mối liên hệ giữa chiều cao và độ dài bàn chân là cao hơn (mạnh hơn) so với mối liên hệ giữa độ dài bàn tay và chiều cao.

Một ví dụ về hồi quy, chúng ta muốn biết mối quan hệ giữa nhiệt độ không khí và tốc độ chạy của thằn lằn. Đặt các con thằn lằn vào một phòng có nhiệt độ là 10oC, đuổi chúng và tiến hành ghi nhận tốc độ chạy của từng con. Thực hiện lặp lại 10 lần các phép thử trên ở các nhiệt độ khác nhau từ 0oC – 20oC. Đây là hồi quy, bởi bạn đã quyết định chọn những nhiệt độ nào để phân tích. Bạn có thể thực hiện phân tích tương quan \({r^2}\), tuy nhiên, điều này là không cần thiết bởi \({r^2}\) phụ thuộc vào giá trị biến độc lập (nhiệt độ) mà bạn chọn. Ngoài ra, cùng một mối quan hệ giống nhau (nhiệt độ và tốc độ chạy) nhưng khoảng nhiệt độ càng hẹp thì giá trị \({r^2}\) càng nhỏ. Điều này được minh họa hệ số \({r^2}\) theo các khoảng nhiệt độ như hình:

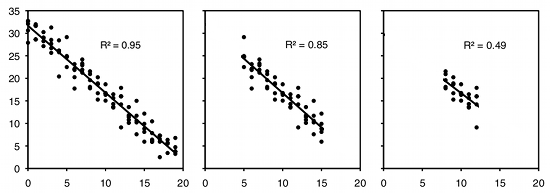
Tuy nhiên, trong một số trường hợp không thể xác định rõ ràng là phân tích tương quan hay phân tích hồi quy. Giả sử ở ví dụ trên cứ mỗi chủ nhật trong 8 tháng bạn ra sa mạc tiến hành đo nhiệt độ, xua đuổi và ghi nhận tốc độ chạy của thằn lằn. Bạn không có chủ động chọn nhiệt độ mà chỉ chấp nhận sự thay đổi nhiệt độ của môi trường. Điều này có vẻ phù hợp với phân tích tương quan. Nhưng bạn không phải chọn mẫu ngẫu nhiên mà chỉ chọn mẫu vào chủ nhật trong 8 tháng (chứ không phải toàn bộ năm), như vậy, nó có phải là hồi quy? Câu trả lời trong trường hợp này là tùy thuộc vào mục đích nghiên cứu của bạn.

Cụ thể:

• Nếu bạn chỉ quan tâm đến p-value để kiểm định giả thuyết thì tương quan và hồi quy là giống nhau.
• Nếu bạn quan tâm đến việc so sánh độ mạnh của các mối liên hệ (\({r^2}\) này so sánh với các \({r^2}\) khác) thì bạn nên sử dụng phân tích tương quan và thiết kế nghiên cứu thực nghiệm đo lường X, Y trên một mẫu ngẫu nhiên.
• Nếu bạn xác định các giá trị X cần nghiên cứu trước thì thực hiện phân tích hồi quy và không nên giải thích \({r^2}\) như là một ước lượng chung về tổng thể mà bạn quan sát.

Còn tiếp…