500 câu trắc nghiệm Kinh tế lượng – 5B

Tổng hợp 500 câu trắc nghiệm + tự luận Kinh tế lượng (Elementary Statistics). Tất cả các câu hỏi trắc nghiệm + tự luận đều có đáp án. Nội dung được khái quát trong 13 phần, mỗi phần gồm 3 bài kiểm tra (A, B, C). Các câu hỏi trắc nghiệm + tự luận bám rất sát chương trình kinh tế lượng, đặc biệt là phần thống kê, rất phù hợp cho các bạn củng cố và mở rộng các kiến thức về Kinh tế lượng. Các câu hỏi trắc nghiệm + tự luận của phần 5B bao gồm:
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Provide an appropriate response.
1) Consider the uniform distribution shown below. Find the probability that x is greater than 6.
Discuss the relationship between area under a density curve and probability.
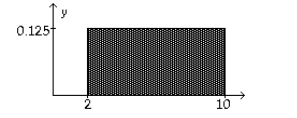
The area under the curve from 6 to 10 is 0.5, thus the probability that x is greater than 6 is 0.5.
2) SAT verbal scores are normally distributed with a mean of 430 and a standard deviation of 120 (based on data from the College Board ATP). (a) If a single student is randomly selected, find the probability that the sample mean is above 500. (b) If a sample of 35 students are selected randomly, find the probability that the sample mean is above 500. These two problems appear to be very similar. Which problem requires the application of the Central Limit theorem, and in what way does the solution process differ between the two problems?
In the first, the student must use the formula \(z = \frac{{x – \mu }}{\sigma }\), whereas in the second problem, the student must use the Central Limit theorem and the formula \(z = \frac{{\bar x – \mu }}{{\frac{\sigma }{{\sqrt n }}}}\), since the problem involves a sample. The probability for the first is 0.2810; for the second, 0.0003.
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
Using the following uniform density curve, answer the question.

3) What is the probability that the random variable has a value between 0.4 and 0.7?
○ 0.088
○ 0.163
○ 0.288
● 0.038
Assume that the weight loss for the first month of a diet program varies between 6 pounds and 12 pounds, and is spread evenly over the range of possibilities, so that there is a uniform distribution. Find the probability of the given range of pounds lost.
4) More than 9 pounds
● 1/2
○ 5/6
○ 2/3
○ 1/7
If Z is a standard normal variable, find the probability.
5) The probability that Z lies between 0.7 and 1.98
○ 0.2175
○ -0.2181
○ 1.7341
● 0.2181
The Precision Scientific Instrument Company manufactures thermometers that are supposed to give readings of 0eC at the freezing point of water. Tests on a large sample of these thermometers reveal that at the freezing point of water, some give readings below 0eC (denoted by negative numbers) and some give readings above 0eC (denoted by positive numbers). Assume that the mean reading is 0eC and the standard deviation of the readings is 1.00eC. Also assume that the frequency distribution of errors closely resembles the normal distribution. A thermometer is randomly selected and tested. Find the temperature reading corresponding to the given information.
6) If 7% of the thermometers are rejected because they have readings that are too low, but all other thermometers are acceptable, find the temperature that separates the rejected thermometers from the others.
○ -1.53
● -1.48
○ -1.26
○ -1.39
Assume that X has a normal distribution, and find the indicated probability.
7) The mean is \(\mu \) = 15.2 and the standard deviation is \(\sigma \) = 0.9. Find the probability that X is between 14.3 and 16.1.
○ 0.8413
● 0.6826
○ 0.3413
○ 0.1587
Solve the problem.
8) In one region, the September energy consumption levels for single-family homes are found to be normally distributed with a mean of 1050 kWh and a standard deviation of 218 kWh. Find P45, which is the consumption level separating the bottom 45% from the top 55%.
○ 1087.8
○ 1148.1
● 1021.7
○ 1078.3
Find the indicated probability.
9) Assume that the weights of quarters are normally distributed with a mean of 5.67 g and a standard deviation 0.070 g. A vending machine will only accept coins weighing between 5.48 g and 5.82 g. What percentage of legal quarters will be rejected?
● 1.96%
○ 1.62%
○ 2.48%
○ 0.0196%
SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. Provide an appropriate response.
10) A poll of 1400 randomly selected students in grades 6 through 8 was conducted and found that 30% enjoy playing sports. Would confidence in the results increase if the sample size were 3200 instead of 1400? Why or why not?
Yes. As the sample size increases, the sample statistics tend to vary less and they tend to be closer to the population parameter.