Hồi quy Poisson – STATA

Hồi quy poisson được sử dụng để ước lượng các mô hình với dữ liệu của biến phụ thuộc có dạng đếm (counts). Ví dụ: chúng ta muốn dự báo số giải thưởng (num_awards) mỗi sinh viên sẽ đạt được theo điểm số các môn học (math) ở từng chuyên ngành (prog). Phần minh họa sử dụng dữ liệu thực hành là poisson.dta use https://www.vietlod.com/data/poisson.dta, clear Bộ dữ liệu bao gồm 3 biến num_awards, math và prog với 200 quan sát. Thông tin cụ thể của các biến như sau: Biến prog là ngành học, có dạng danh mục với 3 giá trị: 1 (tổng quát), 2 (học thuật) và 3 (hướng nghiệp). Biến num_awards là một biến đếm, cho biết số giải thưởng mà sinh viên đạt được. Biến math là điểm thi toán, là 1 biến liên tục. 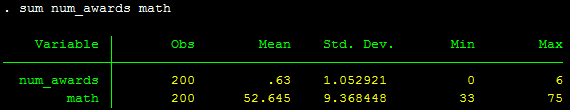sum num_awards math Kết quả thống kê của số giải thưởng ở từng chuyên ngành được thể hiện như hình bên dưới. Theo đó, biến prog là biến giải thích tốt cho biến kết quả, bởi giá trị trung bình của nó thay đổi nhiều ở các chuyên ngành. tabstat num_awards, by(prog) stats(mean sd n) histogram num_awards, discrete freq scheme(s1mono) 1. Lựa chọn phương pháp phân tích Negative binomial regression - có thể được sử dụng khi dữ liệu phân tán quá rộng, nghĩa là phương sai của biến phụ thuộc vượt quá giá trị trung bình của biến. Hồi quy Negative binomial được xem là dạng tổng của hồi quy Poisson. Zero-inflated regression model - được sử dụng khi dữ liệu của biến phụ thuộc tập trung rất gần 0. Mô hình Zero-inflated sẽ ước lượng đồng thời 2 biểu thức theo hồi quy logit (dữ liệu tập trung gần 0) và hồi quy poisson (dữ liệu đếm) Hồi quy OLS - Các biến đếm sẽ được chuyển sang dạng logarit và được đưa vào sử dụng trong phân tích hồi quy tuyến tính OLS. Vì vậy, xảy ra hiện tượng mất mát thông tin, đồng thời phát sinh lỗi trong quá trình logarit hóa (các quan sát có giá trị đếm bằng 0). 2. Thực hiện hồi quy Poisson trên STATA Phần trình bày bên dưới sẽ minh họa cách hồi quy Poisson trên STATA. Hồi quy poisson trên Stata được thự hiện bằng lệnh poisson. Tiền tố i. để xác định biến danh mục cho biến prog đứng sau. Chúng ta sử dụng thêm tùy chọn vce(robust) để kiểm soát hiện tượng phương sai thay đổi theo đề nghị của Cameron and Trivedi (2009). poisson num_awards i.prog math, vce(robust) Phần kết quả bắt đầu với kết quả các quá trình lặp. Chính vì chúng ta sử dụng sai số chuẩn mạnh để kiểm soát vấn đề phương sai thay đổi, do đó, giá trị chúng ta có giá trị log pseudolikelihoods. Giá trị log pseudolikelihood này có thể được sử dụng để so sánh lựa chọn mô hình. Kế tiếp là bảng tổng hợp kết quả về độ phù hợp của mô hình. Thống kê Ward Chi2 với 3 bậc tự do 80.15 cho thấy mô hình đầy đủ với 3 biến giải thích phù hợp hơn so với mô hình không. Kết quả này có ý nghĩa thống kê 1%. Giá trị pseudo-R2 bằng 0.21 cũng được trình bày ở đây. Bên dưới bảng thông tin về độ phù hợp của mô hình là các thông tin về hệ số hồi quy Poisson như hệ số ước lượng, sai số chuẩn, chỉ số z, mức ý nghĩa và khoảng tin cậy 95% của hệ số. Ngoại trừ biến 3.prog, các hệ số của biến math và 2.prog đều có ý nghĩa thống kê. Giá trị hệ số ước lượng của biến math bằng 0.07 cho biết kì vọng tăng 0.07 đơn vị trong giá trị của log num_awards khi biến math tăng 1 đơn vị. Hoặc hệ số của biến 2.prog bằng 1.1 có ý nghĩa rằng so với nhóm prog=1 thì giá trị kì vọng của của log num_awards cao hơn 1.1 lần. Để xác định xem biến bản thân biến prog có ý nghĩa thống kê hay không, chúng ta có thể sử dụng lệnh test như sau: test 2.prog 3.prog ( 1) [num_awards]2.prog = 0 ( 2) [num_awards]3.prog = 0 chi2( 2) = 14.76 Prob > chi2 = 0.0006 Để kiểm tra xem dạng hàm của mô hình có phù hợp với dữ liệu mẫu, chúng ta có thể sử dụng lệnh estat gof để có kết quả về kiểm định độ phù hợp Chi2. Lưu ý, đây không phải là kiểm định hệ số như đã trình bày ở phần kết quả ban đầu. Giả thuyết đặt ra là dạng hàm (poisson) của mô hình phù hợp với dữ liệu mẫu. estat gof Goodness-of-fit chi2 = 189.4496 Prob > chi2(196) = 0.6182 Pearson goodness-of-fit = 212.1437 Prob > chi2(196) = 0.2040 Với mức ý nghĩa 0.6182 trên, chúng ta có thể kết luận rằng hàm poisson phản ánh tốt dữ liệu mẫu. Nếu kết quả kiểm định có ý nghĩa thống kê, chúng ta có thể xem xét các vấn đề liên quan như bỏ sót biến, đa cộng tuyến hoặc dữ liệu phân tán quá mức (over-dispersion). Đôi khi, chúng ta sử dụng dạng tỉ lệ thay vì dạng log của các hệ số để giải thích. Đây chính là dạng mũ hóa các hệ số ước lượng từ phương trình: log(num_awards) = Intercept + b1(prog=2) + b2(prog=3) + b3math. 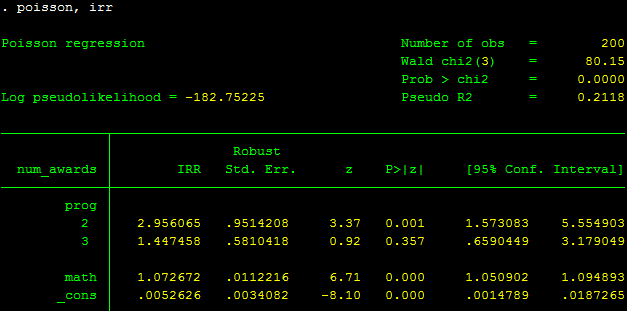Mũ hóa hai vế: num_awards = exp(Intercept + b1(prog=2) + b2(prog=3)+ b3math) = exp(Intercept) * exp(b1(prog=2)) * exp(b2(prog=3)) * exp(b3math) Bằng cách thêm tùy chọn irr phía sau câu lệnh poisson như sau: poisson, irr Kết quả trên cho thấy tỉ lệ IRR cho biến 2.prog gấp 2.96 lần so với nhóm tham chiếu. Đối với biến math, thì một sự gia tăng 1 đơn vị của biến này sẽ làm tăng 7% trong IRR của biến num_awards. Để dễ hiểu và giải thích mô hình, chúng ta sử dụng lệnh margins để tính toán các giá trị đếm dự đoán của biến num_awards tại các mức giá trị của biến prog, trong khi giữ nguyên giá trị các biến còn lại tại giá trị trung bình của biến. 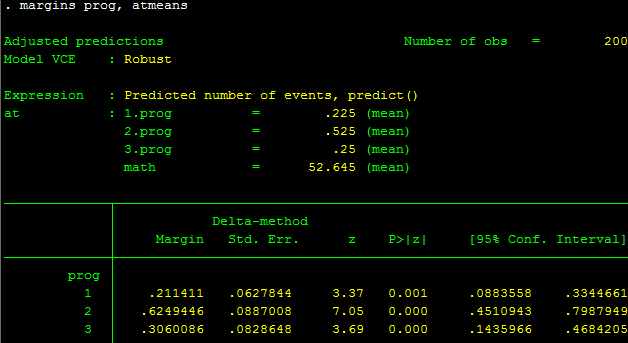margins prog, atmeans Trong bảng kết quả trên, chúng ta thấy rằng số giải thưởng cho prog=1 là 0.21; prog=2 là 0.62 và prog=3 là 0.31 (tại giá trị trung bình của biến math) Hoặc chúng ta cũng có thể dự đoán số giải thưởng theo sự thay đổi điểm math (thay đổi từ 35 đến 75 với bước nhảy là 10). margins, at(math=(35(10)75)) vsquish Bảng kết quả trên cho thấy rằng tại giá trị biến math bằng 35 thì giá trị dự đoán của num_awards là 0.13 và khi giá trị của math bằng 75 thì giá trị dự đoán của num_awards là 2.17. Thông tin chi tiết về mô hình được tổng hợp trong kết quả của lệnh fitstat như sau: fitstat Các bạn có thể minh họa giá trị dự đoán của biến num_awards bằng đồ thị như sau: Kết quả cho thấy, chuyên ngành học thuật (prog=2) được dự đoán có số giải thưởng nhiều nhất, đặc biệt trong trường hợp sinh viên có điểm toán cao. Số giải thưởng được dự báo ít nhất trong ngành tổng quát (prog=1)

Thuyết Nguyễn

Bài liên quan

Hồi quy tuyến tính – OLS – Stata

Kiểm định t-test cặp đôi – Stata

Hồi quy Cluster – STATA

Mô hình tác động cố định – FE