Phân biệt mô hình Logit vs Probit

Đặt vấn đề hồi quy với biến phụ thuộc dạng danh mục

Khi một biến phụ thuộc là biến danh mục (nhị phân, thứ tự hoặc định danh) thì phương pháp bình phương tối thiểu OLS sẽ không còn là một ước lượng không chệch tốt nhất (BLUE) nữa. Điều đó có nghĩa các ước lượng OLS sẽ bị chệch và không hiệu quả. Do đó, các nhà nghiên cứu đã phát triển rất nhiều dạng mô hình hồi quy cho các biến phụ thuộc dạng danh mục.

Mô hình hồi quy cho các biến phụ thuộc dạng danh mục

Tùy theo dạng biến phụ thuộc mà chúng ta những mô hình hồi quy tương ứng như sau:

• Nếu biến phụ thuộc có dạng nhị phân (giá trị 0 và 1) thì mô hình phù hợp là mô hình logit hoặc mô hình probit.
• Nếu biến phụ thuộc có dạng thứ tự (hạng 1, hạng 2, hạng 3…) thì mô hình phù hợp là mô hình logit thứ tự hoặc mô hình probit thứ tự.
• Nếu biến phụ thuộc có dạng định danh thì mô hình sử dụng phù hợp là mô hình logit hoặc probit đa bậc, hoặc mô hình logit có điều kiện.

Các mô hình logit vs probit đều dựa trên phương pháp ước lượng hợp lí tối đa ML (Maximum likelihood). Ước lượng hợp lí tối đa đòi hỏi một giả định về dạng hàm phân phối xác suất, chẳng hạn hàm logit và hàm bù log-log. Các mô hình Logit sử dụng hàm phân phối Logit chuẩn trong khi các mô hình Probit giả định hàm phân phối chuẩn chuẩn hóa. Bài viết này tập trung trình bày một số khía cạnh để phân biệt 2 mô hình Logit vs Probit.

Lựa chọn mô hình Logit vs Probit

Sự khác nhau giữa Logit vs Probit chủ yếu tập trung ở hàm phân phối của các sai số nhiễu.

• Trong mô hình Logit, các sai số được giả định có phân phối Logit chuẩn, \(\lambda (\varepsilon ) = \frac{{{e^z}}}{{{{(1 + {e^z})}^2}}}\).
• Trong khi đó, các sai số của mô hình Probit được giả định tuân theo phân phối chuẩn chuẩn hóa, \(\phi (\varepsilon ) = \frac{1}{{2\pi }}{e^{ – \frac{{{z^2}}}{2}}}\)

Đồ thị phân biệt dạng phân phối của 2 mô hình Logit vs Probit được thể hiện như sau:

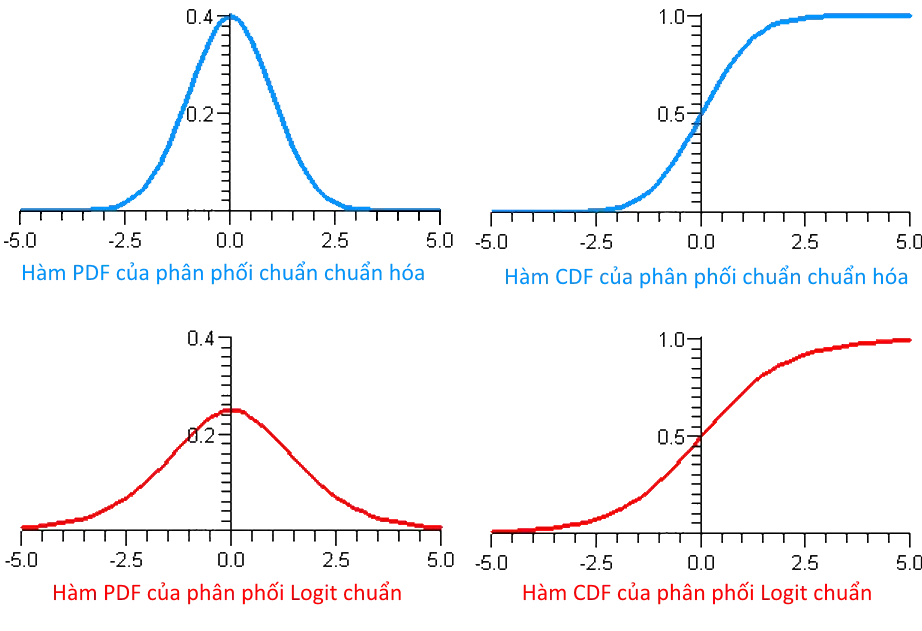
Nhận xét:

Hàm mật độ xác suất (PDF) của phân phối chuẩn chuẩn hóa có đỉnh cao (nhọn) và 2 đuôi hẹp hơn so với hàm mật độ xác suất của phân phối Logit chuẩn. Đồng thời, hàm mật độ xác suất tích lũy (CDF) của phân phối chuẩn chuẩn hóa dốc hơn ở phần giữa so với đường CDF của phân phối Logit chuẩn và rất nhanh để đạt đến giá trị 0 (bên trái) và 1 (bên phải).

Hai mô hình khác nhau, dĩ nhiên, cho các kết quả ước lượng khác nhau. Các ước lượng của mô hình logit xấp xỉ gấp \(\pi /\sqrt 3 \) lần so với các hệ số tương ứng trong mô hình probit. Tuy nhiên, những kết quả ước lượng này gần như không có sự khác biệt về phương sai của các hệ số biến giải thích^[1]

1. Long, J. Scott (1997). Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.