93 câu trắc nghiệm Kinh tế lượng – Phần 2

Tổng hợp 93 câu trắc nghiệm Kinh tế lượng cơ bản trong tài chính bằng tiếng anh (có đáp án kèm theo). Nội dung được phân thành 9 chương, được chia làm 2 phần. Các câu hỏi trắc nghiệm phần 2 bao gồm:
KTL_002_C5_1: Consider the following model estimated for a time series
\({y_t} = 0.3 + 0.5{y_{t – 1}} – 0.4{\varepsilon _{t – 1}} + {\varepsilon _t}\)
where \({\varepsilon _t}\) is a zero mean error process. What is the (unconditional) mean of the series, \({y_t}\)?
● 0.6
○ 0.3
○ 0.0
○ 0.4
KTL_002_C5_2: Consider the following single exponential smoothing model: \({S_t} = \alpha {X_t} + (1 – \alpha ){S_{t – 1}}\)
You are given the following data: \(\hat \alpha = 0.1,{X_t} = 0.5,{S_{t – 1}} = 0.2\)
If we believe that the true DGP can be approximated by the exponential smoothing model, what would be an appropriate 2-step ahead forecast for X? (i.e. a forecast of \({X_{t + 2}}\) made at time t)
○ 0.2
● 0.23
○ 0.5
○ There is insufficient information given in the question to form more than a one step ahead forecast.
KTL_002_C5_3: Consider the following MA(3) process: \({y_t} = 0.1 + 0.4{u_{t – 1}} + 0.2{u_{t – 2}} – 0.1{u_{t – 3}} + {u_t}\)
What is the optimal forecast for \({y_t}\), 3 steps into the future (i.e. for time t+2 if all information until time t-1 is available), if you have the following data? \({u_{t – 1}}\) = 0.3; \({u_{t – 2}}\) = -0.6; \({u_{t – 3}}\) = -0.3
○ 0.4
○ 0.0
● 0.07
○ –0.1
KTL_002_C5_4: Which of the following sets of characteristics would usually best describe an autoregressive process of order 3 (i.e. an AR(3))?
● A slowly decaying acf, and a pacf with 3 significant spikes
○ A slowly decaying pacf and an acf with 3 significant spikes
○ A slowly decaying acf and pacf
○ An acf and a pacf with 3 significant spikes
KTL_002_C5_5: A process, xt, which has a constant mean and variance, and zero autocovariance for all non-zero lags is best described as
● A white noise process
○ A covariance stationary process
○ An autocorrelated process
○ A moving average process
KTL_002_C5_6: Which of the following conditions must hold for the autoregressive part of an ARMA model to be stationary?
● All roots of the characteristic equation must lie outside the unit circle
○ All roots of the characteristic equation must lie inside the unit circle
○ All roots must be smaller than unity
○ At least one of the roots must be bigger than one in absolute value.
KTL_002_C5_7: Which of the following statements are true concerning time-series forecasting?
(i) All time-series forecasting methods are essentially extrapolative.
(ii) Forecasting models are prone to perform poorly following a structural break in a series.
(iii) Forecasting accuracy often declines with prediction horizon.
(iv) The mean squared errors of forecasts are usually very highly correlated with the profitability of employing those forecasts in a trading strategy.
○ (i), (ii), (iii), and (iv)
● (i), (ii) and (iii) only
○ (ii), (iii) only
○ (ii) and (iv) only
KTL_002_C5_8: If a series, yt, follows a random walk (with no drift), what is the optimal 1-step ahead forecast for y?
● The current value of y.
○ Zero.
○ The historical unweighted average of y.
○ An exponentially weighted average of previous values of y.
KTL_002_C5_9: Consider a series that follows an MA(1) with zero mean and a moving average coefficient of 0.4. What is the value of the autocorrelation function at lag 1?
○ 0.4
○ 1
● 0.34
○ It is not possible to determine the value of the autocovariances without knowing the disturbance variance.
KTL_002_C5_10: Which of the following statements are true?
(i) An MA(q) can be expressed as an AR(infinity) if it is invertible
(ii) An AR(p) can be written as an MA(infinity) if it is stationary
(iii) The (unconditional) mean of an ARMA process will depend only on the intercept and on the AR coefficients and not on the MA coefficients
(iv) A random walk series will have zero pacf except at lag 1
○ (ii) and (iv) only
○ (i) and (iii) only
○ (i), (ii), and (iii) only
● (i), (ii), (iii), and (iv).
KTL_002_C5_11: Consider the following picture and suggest the model from the following list that best characterises the process:
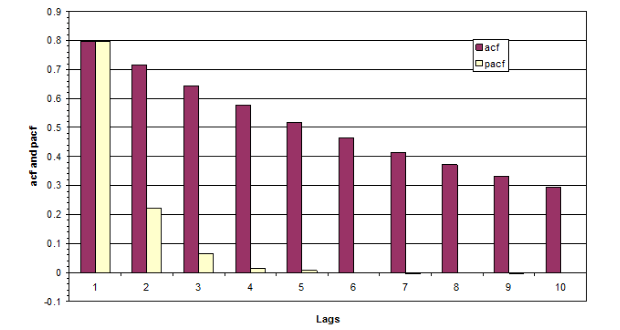
○ An AR(1)
○ An AR(2)
● An ARMA(1,1)
○ An MA(3)
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was \({y_t} = 0.9{y_{t – 1}} – 0.3{u_{t – 1}} + {u_t}\).
KTL_002_C5_12: Which of the following models can be estimated using ordinary least squares?
(i) An AR(1)
(ii) An ARMA(2,0)
(iii) An MA(1)
(iv) An ARMA(1,1)
○ (i) only
● (i) and (ii) only
○ (i), (ii), and (iii) only
○ (i), (ii), (iii), and (iv).
KTL_002_C5_13: If a series, y, is described as “mean-reverting”, which model from the following list is likely to produce the best long-term forecasts for that series y?
○ A random walk
● The long term mean of the series
○ A model from the ARMA family
○ A random walk with drift
KTL_002_C5_14: Consider the following AR(2) model. What is the optimal 2-step ahead forecast for y if all information available is up to and including time t, if the values of y at time t, t-1 and t-2 are –0.3, 0.4 and –0.1 respectively, and the value of u at time t-1 is 0.3?
\({y_t} = – 0.1 + 0.75{y_{t – 1}} – 0.125{y_{t – 2}} + {u_t}\)
○ -0.1
○ 0.27
● -0.34
○ 0.30
KTL_002_C5_15: What is the optimal three-step ahead forecast from the AR(2) model given in question 14?
○ -0.1
○ 0.27
○ -0.34
● -0.31
KTL_002_C5_16: Suppose you had to guess at the most likely value of a one hundred step-ahead forecast for the AR(2) model given in question 14 – what would your forecast be?
○ -0.1
○ 0.7
● –0.27
○ 0.75