Kiểm định Kruskal-Wallis
Kiểm định Kruskal-Wallis trong thực hành kinh tế lượng với SPSS

Tóm tắt: Kiểm định Kruskal-Wallis là công cụ quan trọng trong thực hành kinh tế lượng khi cần so sánh sự khác nhau về giá trị trung bình của một biến phụ thuộc theo nhiều nhóm mà không yêu cầu phân phối chuẩn. Đây là phương pháp thay thế phi tham số cho phân tích phương sai một chiều ANOVA và mở rộng của kiểm định Mann-Whitney U cho nhiều nhóm độc lập.
Giới thiệu về kiểm định Kruskal-Wallis
Nội dung chính
- Giới thiệu về kiểm định Kruskal-Wallis
- Giả thiết của kiểm định Kruskal-Wallis
- Ví dụ thực tế từ kinh tế Việt Nam
- Dữ liệu mẫu và mô tả
- Hướng dẫn thực hành chi tiết trên SPSS
- Giải thích kết quả kiểm định
- Lưu ý và cảnh báo quan trọng
- Ứng dụng mở rộng trong kinh tế
- Tổng kết
- Phụ lục: Code thực hiện trên các phần mềm khác
- Tài liệu tham khảo
Trong nghiên cứu kinh tế lượng, chúng ta thường gặp những tình huống cần so sánh sự khác nhau về một chỉ tiêu kinh tế giữa nhiều nhóm khác nhau. Ví dụ, khi nghiên cứu thu nhập của người lao động theo các lĩnh vực kinh tế khác nhau như nông nghiệp, công nghiệp và dịch vụ, dữ liệu thu nhập thường không tuân theo phân phối chuẩn do tính chất bất đối xứng và có nhiều giá trị ngoại lệ.
Kiểm định Kruskal-Wallis được William Kruskal và W. Allen Wallis phát triển vào năm 1952, là một phương pháp thống kê phi tham số mạnh mẽ để giải quyết vấn đề này. Khác với phân tích phương sai một chiều ANOVA, kiểm định này không yêu cầu giả thiết về phân phối chuẩn của dữ liệu.Mối quan hệ với các kiểm định khác
- Thay thế cho ANOVA một chiều: Khi dữ liệu không đáp ứng giả thiết phân phối chuẩn
- Mở rộng của Mann-Whitney U: Từ 2 nhóm độc lập lên nhiều nhóm (≥ 3 nhóm)
- Tương đương với Wilcoxon-Mann-Whitney: Khi chỉ có 2 nhóm so sánh
- Liên quan đến kiểm định Friedman: Dành cho dữ liệu có khối (block design)
Giả thiết của kiểm định Kruskal-Wallis
Để áp dụng kiểm định Kruskal-Wallis một cách chính xác trong thực hành kinh tế lượng, dữ liệu cần đáp ứng bốn giả thiết cơ bản sau:
Giả thiết 1: Loại biến phụ thuộc
Biến phụ thuộc phải là biến thứ tự hoặc biến liên tục. Trong kinh tế, điều này bao gồm:- Biến liên tục: Thu nhập, chi tiêu, GDP, lạm phát, tỷ lệ thất nghiệp
- Biến thứ tự: Mức độ hài lòng (rất không hài lòng, không hài lòng, trung bình, hài lòng, rất hài lòng)
- Biến định danh có thể sắp xếp: Trình độ học vấn (tiểu học, trung học, đại học, sau đại học)
Giả thiết 2: Biến độc lập phân loại
Biến độc lập là biến phân loại có từ 2 mức trở lên. Các ví dụ trong bối cảnh kinh tế Việt Nam:- Lĩnh vực kinh tế: Nông nghiệp, công nghiệp, dịch vụ
- Vùng kinh tế: Đồng bằng sông Hồng, Bắc Trung bộ, Duyên hải miền Trung, Tây Nguyên, Đông Nam bộ, Đồng bằng sông Cửu Long
- Loại hình doanh nghiệp: Nhà nước, tư nhân, FDI, hợp tác xã
- Thị trường xuất khẩu: ASEAN, EU, Trung Quốc, Hoa Kỳ, Nhật Bản
Giả thiết 3: Tính độc lập của quan sát
Các quan sát phải độc lập với nhau, không có mối quan hệ giữa các quan sát trong cùng một nhóm hoặc giữa các nhóm khác nhau. Điều này đòi hỏi:
Giả thiết 4: Dạng phân phối tương đồng
Mặc dù không yêu cầu phân phối chuẩn, dạng phân phối của biến phụ thuộc trong các nhóm nên tương đồng. Điều này được kiểm tra thông qua biểu đồ histogram hoặc boxplot.
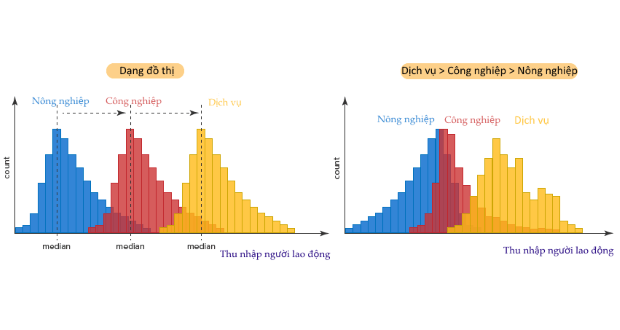
Theo hình minh họa trên, phân phối của biến thu nhập người lao động trong các lĩnh vực công nghiệp, nông nghiệp và dịch vụ có dạng tương đồng nhau (biểu đồ bên trái). Tuy nhiên, ở biểu đồ phải, mặc dù có dạng giống nhau nhưng vị trí phân phối ở 3 nhóm có sự khác biệt rõ rệt. Thu nhập của lao động có xu hướng giảm dần theo thứ tự: dịch vụ – công nghiệp – nông nghiệp.
Ví dụ thực tế từ kinh tế Việt Nam
Để minh họa ứng dụng của kiểm định Kruskal-Wallis trong thực hành kinh tế lượng, chúng ta sẽ phân tích một bài toán cụ thể về thu nhập lao động tại Việt Nam:
Bối cảnh nghiên cứu
Theo báo cáo của Tổng cục Thống kê Việt Nam, cơ cấu kinh tế nước ta đã có những thay đổi đáng kể trong những năm gần đây. Tỷ trọng của lĩnh vực dịch vụ ngày càng tăng, trong khi nông nghiệp có xu hướng giảm. Điều này đặt ra câu hỏi: Liệu thu nhập của người lao động có thật sự khác biệt giữa các lĩnh vực kinh tế?
Câu hỏi nghiên cứu
Chúng ta muốn kiểm tra giả thuyết: “Thu nhập của người lao động không có sự khác biệt có ý nghĩa thống kê giữa các lĩnh vực nông nghiệp, công nghiệp và dịch vụ”
Giả thuyết thống kê
Phát biểu chính thức các giả thuyết kiểm định:
- Giả thuyết không (H0): $H_0$: Không có sự khác nhau về thu nhập trung vị của người lao động giữa các lĩnh vực kinh tế
- Giả thuyết đối (H1): $H_1$: Có ít nhất một cặp lĩnh vực có sự khác biệt về thu nhập trung vị có ý nghĩa thống kê
Dữ liệu mẫu và mô tả
Nghiên cứu sử dụng bộ dữ liệu từ Khảo sát Lao động Việc làm Quốc gia, bao gồm thông tin về 7,287 người lao động trên toàn quốc. Đây là một mẫu đại diện cho tổng thể lao động Việt Nam.
Tải xuống dữ liệu Kruskal-WallisCác biến trong nghiên cứu
Bộ dữ liệu chứa các thông tin quan trọng sau:
- gender: Giới tính (nam/nữ)
- age: Tuổi của người lao động
- ethnic: Dân tộc
- degree: Trình độ học vấn
- region: Vùng miền địa lý
- urban: Khu vực thành thị/nông thôn
- school: Số năm đi học
- exp: Số năm kinh nghiệm làm việc
- section: Loại hình doanh nghiệp
- structure: Lĩnh vực kinh tế (1 = Dịch vụ, 2 = Công nghiệp, 3 = Nông nghiệp)
- earn: Thu nhập hàng năm (triệu đồng)
Thống kê mô tả sơ bộ
Trước khi thực hiện kiểm định chính thức, việc khám phá dữ liệu thông qua thống kê mô tả là cần thiết để hiểu rõ đặc điểm của từng nhóm.
Hướng dẫn thực hành chi tiết trên SPSS
Quá trình thực hiện kiểm định Kruskal-Wallis trên SPSS bao gồm các bước kiểm tra giả thiết và thực hiện kiểm định chính thức. Dưới đây là hướng dẫn từng bước chi tiết:
Bước 1: Kiểm tra giả thiết về dạng phân phối
Trước khi thực hiện kiểm định Kruskal-Wallis, cần kiểm tra dạng phân phối của biến thu nhập earn theo biến lĩnh vực kinh tế structure bằng biểu đồ histogram.
Thực hiện các bước sau:
- Vào menu Graphs → Legacy dialogs → Histogram…
- Đưa biến thu nhập
earnvào ô Variable - Đưa biến lĩnh vực
structurevào ô Panel by - Thiết lập Columns để hiển thị các biểu đồ cạnh nhau
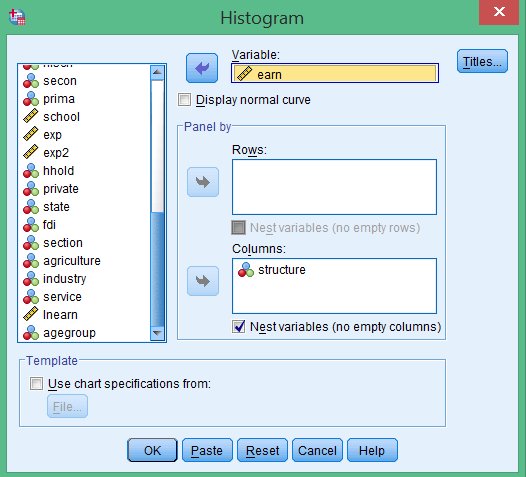
Bước 2: Phân tích biểu đồ histogram
Sau khi tạo biểu đồ, kết quả hiển thị như sau:
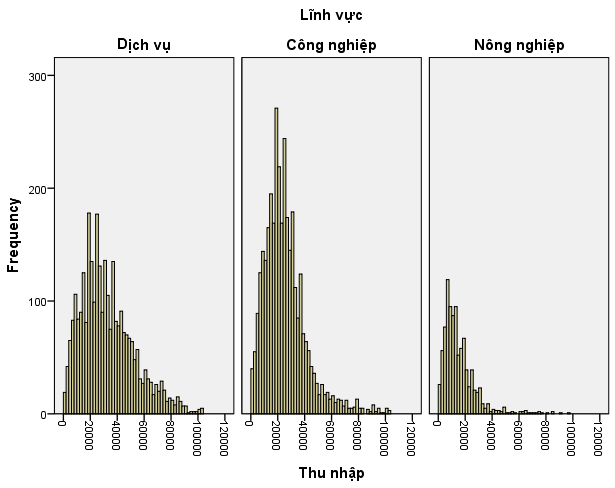
Từ biểu đồ histogram, chúng ta có thể rút ra những nhận xét quan trọng sau:
- Dạng phân phối tương đồng: Các biểu đồ thu nhập ở ba lĩnh vực có hình dạng tương đối giống nhau (đều lệch phải)
- Khác biệt về vị trí: Thu nhập trong lĩnh vực dịch vụ và công nghiệp tập trung ở mức 20-40 triệu đồng/năm
- Nông nghiệp thu nhập thấp: Thu nhập trong lĩnh vực nông nghiệp chủ yếu tập trung ở mức dưới 20 triệu đồng/năm
- Dịch vụ có thu nhập cao: Lĩnh vực dịch vụ có phân bố thu nhập trải rộng hơn ở các mức cao
Tổng kết: Thu nhập của người lao động có xu hướng giảm dần theo thứ tự dịch vụ > công nghiệp > nông nghiệp.
Bước 3: Thực hiện kiểm định Kruskal-Wallis
Sau khi xác nhận dữ liệu đáp ứng các giả thiết, tiến hành thực hiện kiểm định chính thức:
Truy cập menu theo đường dẫn:
Analyze → Nonparametric Tests → Legacy Dialogs → K Independent Samples…
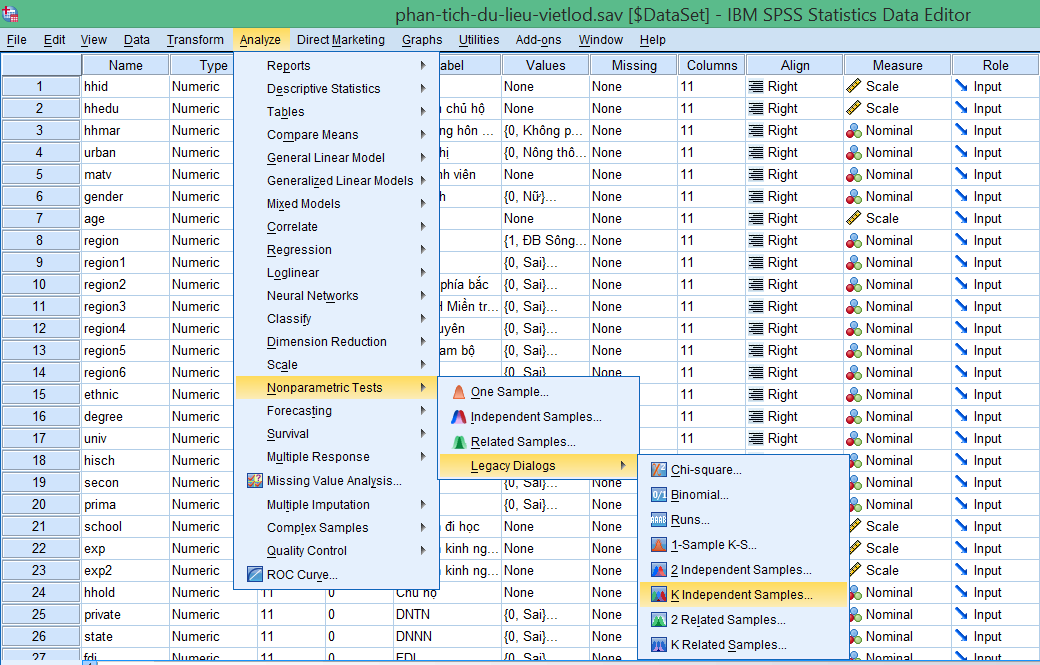
Bước 4: Cấu hình kiểm định
Cửa sổ Tests for Several Independent Samples sẽ xuất hiện. Thực hiện các thiết lập sau:
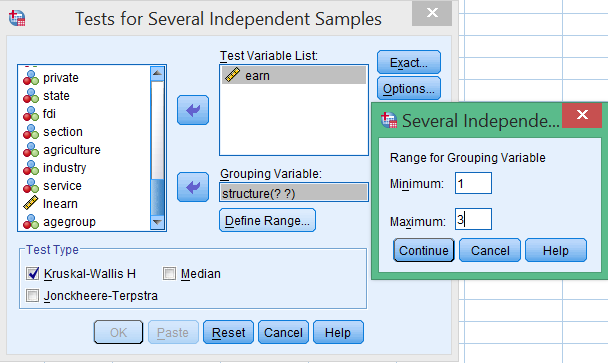
- Kéo biến thu nhập
earnvào ô Test Variable List - Kéo biến lĩnh vực
structurevào ô Grouping Variable - Bấm Define Groups… để thiết lập các nhóm
- Thiết lập Minimum: 1 và Maximum: 3 (tương ứng với 3 lĩnh vực)
- Đảm bảo Kruskal-Wallis H được chọn trong phần Test Type
Bước 5: Thiết lập tùy chọn Statistics
Bấm Options… để thiết lập các thống kê bổ sung:
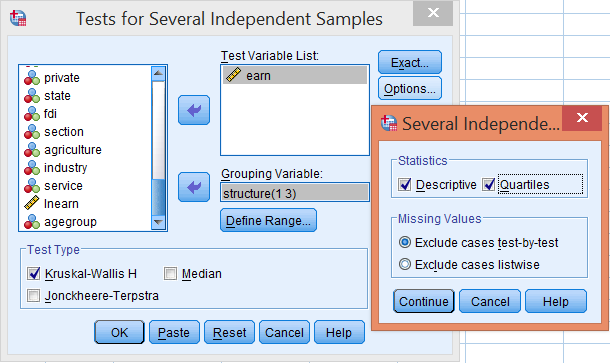
- Chọn Descriptive để hiển thị thống kê mô tả
- Chọn Quartiles để hiển thị các tứ phân vị
- Bấm Continue để xác nhận
- Bấm OK để thực hiện kiểm định
Giải thích kết quả kiểm định
Sau khi thực hiện kiểm định, SPSS sẽ xuất ra kết quả chi tiết về sự khác biệt thu nhập trung vị giữa ba lĩnh vực kinh tế:
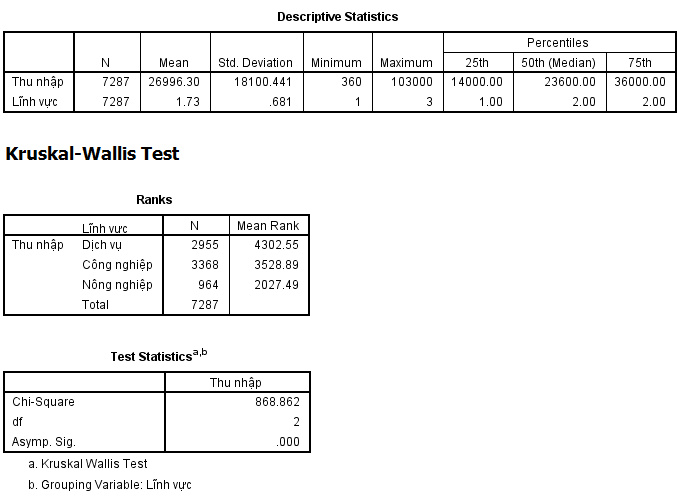
Phân tích bảng Ranks
Bảng Ranks cung cấp thông tin về mean rank của từng lĩnh vực:
- Lĩnh vực dịch vụ (structure=1): Mean Rank = 4302.55
- Lĩnh vực công nghiệp (structure=2): Mean Rank = 3528.89
- Lĩnh vực nông nghiệp (structure=3): Mean Rank = 2027.49
Kết quả cho thấy rõ ràng sự phân tầng thu nhập: dịch vụ có thu nhập cao nhất, tiếp theo là công nghiệp, và thấp nhất là nông nghiệp.
Phân tích bảng Test Statistics
Bảng Test Statistics chứa các thông tin quan trọng để ra quyết định thống kê:
- Thống kê $\chi^2$: Chi-Square (χ²) = 868.862
- Bậc tự do: Degrees of freedom (df) = 2
- Giá trị p xấp xỉ: Asymp. Sig. (p-value) = 0.000
Quyết định thống kê
Với mức ý nghĩa α = 0.05:
Ý nghĩa thực tiễn
Kết quả kiểm định phản ánh thực trạng cơ cấu kinh tế Việt Nam:
- Chuyển dịch cơ cấu kinh tế: Xu hướng phát triển dịch vụ tạo ra thu nhập cao hơn
- Hiện đại hóa công nghiệp: Lĩnh vực công nghiệp đang dần cải thiện thu nhập
- Thách thức nông nghiệp: Cần có chính sách hỗ trợ nâng cao thu nhập nông dân
- Bất bình đẳng thu nhập: Sự chênh lệch thu nhập giữa các lĩnh vực cần được quan tâm
Lưu ý và cảnh báo quan trọng
Khi thực hiện và giải thích kết quả kiểm định Kruskal-Wallis trong thực hành kinh tế lượng, cần lưu ý những điểm sau:
Về kích thước mẫu
Về giải thích kết quả
- So sánh median, không phải mean: Kiểm định so sánh trung vị các nhóm, không phải trung bình cộng
- Kiểm định tổng thể: Chỉ cho biết có ít nhất một cặp nhóm khác biệt, không chỉ rõ nhóm nào
- Cần post-hoc test: Để xác định nhóm nào khác biệt, cần thực hiện kiểm định post-hoc
- Không chứng minh nhân quả: Chỉ cho thấy mối liên hệ, không chứng minh nhân quả
Về các giả thiết
- Bỏ qua kiểm tra giả thiết về dạng phân phối tương đồng
- Không kiểm tra tính độc lập của quan sát
- Nhầm lẫn giữa so sánh mean và median
- Không thực hiện kiểm định post-hoc khi cần thiết
- Giải thích sai ý nghĩa của mean rank
Kiểm định post-hoc
Khi kiểm định Kruskal-Wallis có ý nghĩa thống kê, cần thực hiện kiểm định post-hoc để xác định nhóm nào khác biệt với nhóm nào:
- Dunn’s test: Phương pháp phổ biến nhất cho kiểm định post-hoc
- Mann-Whitney U pairwise: So sánh từng cặp với điều chỉnh Bonferroni
- Conover’s test: Thay thế cho Dunn’s test với một số ưu điểm
Ứng dụng mở rộng trong kinh tế
Kiểm định Kruskal-Wallis có nhiều ứng dụng quan trọng trong các lĩnh vực kinh tế khác nhau:
Kinh tế lao động
- Phân tích mức lương: So sánh lương theo ngành nghề, trình độ học vấn
- Thị trường lao động: Đánh giá tác động của các chính sách việc làm
- Đào tạo nghề: Hiệu quả của các chương trình đào tạo
Kinh tế vĩ mô
- Tăng trưởng kinh tế: So sánh GDP bình quân đầu người giữa các vùng miền
- Lạm phát: Phân tích chỉ số giá tiêu dùng theo khu vực
- Đầu tư công: Hiệu quả của các dự án đầu tư theo ngành
Kinh tế doanh nghiệp
- Hiệu quả sản xuất: So sánh năng suất theo loại hình doanh nghiệp
- Nghiên cứu thị trường: Phân tích sự hài lòng khách hàng
- Quản lý chất lượng: Đánh giá hiệu quả của các phương pháp cải tiến
Tổng kết
Kiểm định Kruskal-Wallis là một công cụ mạnh mẽ và linh hoạt trong thực hành kinh tế lượng, đặc biệt phù hợp khi dữ liệu không đáp ứng giả thiết phân phối chuẩn của phân tích phương sai truyền thống. Phương pháp này cung cấp:
- Tính linh hoạt cao: Không yêu cầu giả thiết phân phối chuẩn
- Khả năng ứng dụng rộng: Phù hợp với nhiều loại dữ liệu kinh tế
- Độ tin cậy cao: Ít bị ảnh hưởng bởi giá trị ngoại lệ
- Dễ thực hiện: Quy trình thực hiện đơn giản trên SPSS
Tuy nhiên, việc áp dụng kiểm định cần tuân thủ nghiêm ngặt các giả thiết và kết hợp với các phương pháp phân tích bổ sung để có được bức tranh toàn diện về vấn đề nghiên cứu. Kết quả kiểm định chỉ là bước đầu, cần có phân tích sâu hơn về ý nghĩa kinh tế và chính sách.
Key Points:
- Kiểm định Kruskal-Wallis thay thế ANOVA khi dữ liệu không có phân phối chuẩn
- So sánh median (trung vị) giữa các nhóm, không phải mean (trung bình)
- Yêu cầu dạng phân phối tương đồng giữa các nhóm
- Kết quả có ý nghĩa cần thêm post-hoc test để xác định nhóm khác biệt
- Phù hợp với dữ liệu kinh tế thường có giá trị ngoại lệ
Phụ lục: Code thực hiện trên các phần mềm khác
Để hỗ trợ người đọc thực hiện kiểm định Kruskal-Wallis trên nhiều phần mềm thống kê khác nhau, phần này cung cấp code tương ứng cho SPSS Syntax, Stata, R và Python.
SPSS Syntax
SPSS Syntax (.sps file)
* Kiểm định Kruskal-Wallis trong SPSS Syntax
* Tác giả: Thực hành kinh tế lượng
* Ngày: 2025
* Mở file dữ liệu
GET FILE='/data/2-way-anova.sav'.
* Mô tả dữ liệu theo nhóm
DESCRIPTIVES VARIABLES=earn
/STATISTICS=MEAN STDDEV MIN MAX
/SORT=MEAN (A).
* Kiểm tra phân phối bằng histogram
GRAPH
/HISTOGRAM(NORMAL)=earn
/PANEL ROWVAR=structure ROWOP=CROSS.
* Thực hiện kiểm định Kruskal-Wallis
NPAR TESTS
/K-W=earn BY structure(1 3)
/STATISTICS DESCRIPTIVES QUARTILES
/MISSING ANALYSIS.
* Thống kê mô tả chi tiết theo nhóm
MEANS TABLES=earn BY structure
/CELLS=MEAN COUNT STDDEV MEDIAN
/STATISTICS ANOVA.
* Kiểm định post-hoc (nếu cần)
* Sử dụng Mann-Whitney U cho từng cặp
NPAR TESTS
/M-W=earn BY structure(1 2)
/MISSING ANALYSIS.
NPAR TESTS
/M-W=earn BY structure(1 3)
/MISSING ANALYSIS.
NPAR TESTS
/M-W=earn BY structure(2 3)
/MISSING ANALYSIS.
* Xuất kết quả
DISPLAY "Kiểm định Kruskal-Wallis hoàn tất".
Stata
Stata (.do file)
* Kiểm định Kruskal-Wallis trong Stata
* Tác giả: Thực hành kinh tế lượng
* Ngày: 2025
* Mở file dữ liệu (chuyển đổi từ SPSS)
use "kruskal_wallis.dta", clear
* Mô tả dữ liệu
describe earn structure
summarize earn, detail
* Thống kê mô tả theo nhóm
by structure, sort: summarize earn, detail
* Kiểm tra phân phối bằng histogram
histogram earn, by(structure) normal ///
title("Phân phối thu nhập theo lĩnh vực") ///
xtitle("Thu nhập (triệu đồng)") ///
ytitle("Mật độ")
* Boxplot để so sánh
graph box earn, over(structure) ///
title("So sánh thu nhập theo lĩnh vực") ///
ytitle("Thu nhập (triệu đồng)")
* Thực hiện kiểm định Kruskal-Wallis
kwallis earn, by(structure)
* Kiểm định post-hoc bằng Dunn's test
* Cần cài đặt package dunntest
* ssc install dunntest
dunntest earn, by(structure) ma(bonferroni)
* Thống kê chi tiết
tabstat earn, by(structure) statistics(n mean sd min max median q)
* Kiểm tra tính đồng nhất phương sai (để so sánh)
robvar earn, by(structure)
* Xuất kết quả
display "Kiểm định Kruskal-Wallis hoàn tất"
display "Mean ranks được sử dụng để so sánh các nhóm"
R
R Script (.R file)
# Kiểm định Kruskal-Wallis trong R
# Tác giả: Thực hành kinh tế lượng
# Ngày: 2025
# Cài đặt và load các package cần thiết
if (!require(foreign)) install.packages("foreign")
if (!require(dplyr)) install.packages("dplyr")
if (!require(ggplot2)) install.packages("ggplot2")
if (!require(FSA)) install.packages("FSA")
if (!require(dunn.test)) install.packages("dunn.test")
library(foreign)
library(dplyr)
library(ggplot2)
library(FSA)
library(dunn.test)
# Đọc dữ liệu từ file SPSS
data <- read.spss("2-way-anova.sav", to.data.frame = TRUE)
# Kiểm tra cấu trúc dữ liệu
str(data)
head(data)
# Thống kê mô tả theo nhóm
summary_stats <- data %>%
group_by(structure) %>%
summarise(
n = n(),
mean = mean(earn, na.rm = TRUE),
median = median(earn, na.rm = TRUE),
sd = sd(earn, na.rm = TRUE),
min = min(earn, na.rm = TRUE),
max = max(earn, na.rm = TRUE),
q1 = quantile(earn, 0.25, na.rm = TRUE),
q3 = quantile(earn, 0.75, na.rm = TRUE)
)
print("Thống kê mô tả theo lĩnh vực:")
print(summary_stats)
# Vẽ boxplot
ggplot(data, aes(x = factor(structure), y = earn)) +
geom_boxplot(fill = "lightblue", alpha = 0.7) +
labs(title = "Phân phối thu nhập theo lĩnh vực kinh tế",
x = "Lĩnh vực (1=Dịch vụ, 2=Công nghiệp, 3=Nông nghiệp)",
y = "Thu nhập (triệu đồng)") +
theme_minimal()
# Vẽ histogram
ggplot(data, aes(x = earn)) +
geom_histogram(bins = 30, fill = "skyblue", alpha = 0.7) +
facet_wrap(~structure, ncol = 3) +
labs(title = "Histogram thu nhập theo lĩnh vực",
x = "Thu nhập (triệu đồng)",
y = "Tần số") +
theme_minimal()
# Thực hiện kiểm định Kruskal-Wallis
kruskal_result <- kruskal.test(earn ~ structure, data = data)
print("Kết quả kiểm định Kruskal-Wallis:")
print(kruskal_result)
# Kiểm định post-hoc bằng Dunn's test
dunn_result <- dunn.test(data$earn, data$structure,
method = "bonferroni", alpha = 0.05)
print("Kết quả kiểm định post-hoc (Dunn's test):")
# Tính effect size (eta-squared)
eta_squared <- kruskal_result$statistic / (nrow(data) - 1)
cat("Effect size (eta-squared):", eta_squared, "\n")
# Kiểm định Levene để kiểm tra homogeneity of variance
levene_result <- car::leveneTest(earn ~ factor(structure), data = data)
print("Kiểm định Levene (homogeneity of variance):")
print(levene_result)
# Tạo bảng kết quả đẹp
results_table <- data.frame(
Statistic = c("Chi-square", "df", "p-value", "Effect size"),
Value = c(kruskal_result$statistic,
kruskal_result$parameter,
kruskal_result$p.value,
eta_squared)
)
print("Bảng tóm tắt kết quả:")
print(results_table)
# Kết luận
alpha <- 0.05
if (kruskal_result$p.value < alpha) {
cat("\nKết luận: Với p-value =", kruskal_result$p.value,
"< α =", alpha, "\n") cat("Bác bỏ giả thuyết H0. Có sự khác biệt có ý nghĩa thống kê.\n") } else { cat("\nKết luận: Với p-value =", kruskal_result$p.value, ">= α =", alpha, "\n")
cat("Không bác bỏ giả thuyết H0. Không có sự khác biệt có ý nghĩa thống kê.\n")
}
Python
Python Script (.py file)
# Kiểm định Kruskal-Wallis trong Python
# Tác giả: Thực hành kinh tế lượng
# Ngày: 2025
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
import scikit_posthocs as sp
# Đọc dữ liệu từ file SPSS
try:
data = pd.read_spss('2-way-anova.sav')
except:
# Nếu không có pyreadstat, tạo dữ liệu mẫu
print("Tạo dữ liệu mẫu...")
np.random.seed(42)
n = 7287
structure = np.random.choice([1, 2, 3], n, p=[0.4, 0.35, 0.25])
# Tạo thu nhập với sự khác biệt giữa các nhóm
earn = np.zeros(n)
for i in range(n):
if structure[i] == 1: # Dịch vụ
earn[i] = np.random.gamma(2, 20) + 10
elif structure[i] == 2: # Công nghiệp
earn[i] = np.random.gamma(2, 15) + 5
else: # Nông nghiệp
earn[i] = np.random.gamma(2, 10) + 2
data = pd.DataFrame({
'earn': earn,
'structure': structure
})
# Kiểm tra dữ liệu
print("Thông tin dữ liệu:")
print(data.info())
print("\nMẫu dữ liệu:")
print(data.head(10))
# Thống kê mô tả theo nhóm
print("\nThống kê mô tả theo lĩnh vực:")
summary_stats = data.groupby('structure')['earn'].agg([
'count', 'mean', 'median', 'std', 'min', 'max',
lambda x: x.quantile(0.25), # Q1
lambda x: x.quantile(0.75) # Q3
]).round(2)
summary_stats.columns = ['n', 'mean', 'median', 'std', 'min', 'max', 'Q1', 'Q3']
print(summary_stats)
# Vẽ biểu đồ
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Boxplot
axes[0, 0].boxplot([data[data['structure'] == i]['earn'] for i in [1, 2, 3]],
labels=['Dịch vụ', 'Công nghiệp', 'Nông nghiệp'])
axes[0, 0].set_title('Boxplot thu nhập theo lĩnh vực')
axes[0, 0].set_ylabel('Thu nhập (triệu đồng)')
# Histogram
for i, sector in enumerate(['Dịch vụ', 'Công nghiệp', 'Nông nghiệp']):
sector_data = data[data['structure'] == i+1]['earn']
axes[0, 1].hist(sector_data, alpha=0.7, label=sector, bins=30)
axes[0, 1].set_title('Histogram thu nhập theo lĩnh vực')
axes[0, 1].set_xlabel('Thu nhập (triệu đồng)')
axes[0, 1].set_ylabel('Tần số')
axes[0, 1].legend()
# Violin plot
data_for_violin = [data[data['structure'] == i]['earn'] for i in [1, 2, 3]]
axes[1, 0].violinplot(data_for_violin, positions=[1, 2, 3])
axes[1, 0].set_title('Violin plot thu nhập theo lĩnh vực')
axes[1, 0].set_ylabel('Thu nhập (triệu đồng)')
axes[1, 0].set_xticks([1, 2, 3])
axes[1, 0].set_xticklabels(['Dịch vụ', 'Công nghiệp', 'Nông nghiệp'])
# QQ plot để kiểm tra phân phối chuẩn
stats.probplot(data['earn'], dist="norm", plot=axes[1, 1])
axes[1, 1].set_title('Q-Q Plot để kiểm tra phân phối chuẩn')
plt.tight_layout()
plt.show()
# Kiểm tra giả thiết về phân phối chuẩn
print("\nKiểm định Shapiro-Wilk cho từng nhóm:")
for i in [1, 2, 3]:
sector_data = data[data['structure'] == i]['earn']
if len(sector_data) > 3: # Shapiro-Wilk cần ít nhất 3 quan sát
shapiro_stat, shapiro_p = stats.shapiro(sector_data[:5000]) # Giới hạn mẫu
print(f"Lĩnh vực {i}: Shapiro-Wilk statistic = {shapiro_stat:.4f}, p-value = {shapiro_p:.4f}")
# Thực hiện kiểm định Kruskal-Wallis
group1 = data[data['structure'] == 1]['earn']
group2 = data[data['structure'] == 2]['earn']
group3 = data[data['structure'] == 3]['earn']
kruskal_stat, kruskal_p = stats.kruskal(group1, group2, group3)
print(f"\nKết quả kiểm định Kruskal-Wallis:")
print(f"Test statistic (H): {kruskal_stat:.6f}")
print(f"P-value: {kruskal_p:.6f}")
print(f"Degrees of freedom: {len([group1, group2, group3]) - 1}")
# Tính effect size (eta-squared)
n_total = len(data)
eta_squared = (kruskal_stat - len([group1, group2, group3]) + 1) / (n_total - len([group1, group2, group3]))
print(f"Effect size (eta-squared): {eta_squared:.6f}")
# Kiểm định post-hoc bằng Dunn's test
print("\nKiểm định post-hoc (Dunn's test):")
dunn_results = sp.posthoc_dunn(data, val_col='earn', group_col='structure',
p_adjust='bonferroni')
print(dunn_results)
# Tính mean ranks
from scipy.stats import rankdata
ranks = rankdata(data['earn'])
data['ranks'] = ranks
mean_ranks = data.groupby('structure')['ranks'].mean()
print("\nMean ranks:")
for i in [1, 2, 3]:
print(f"Lĩnh vực {i}: {mean_ranks[i]:.2f}")
# Tạo bảng kết quả tóm tắt
results_summary = pd.DataFrame({
'Lĩnh vực': ['Dịch vụ', 'Công nghiệp', 'Nông nghiệp'],
'N': [len(group1), len(group2), len(group3)],
'Mean': [group1.mean(), group2.mean(), group3.mean()],
'Median': [group1.median(), group2.median(), group3.median()],
'Mean Rank': [mean_ranks[1], mean_ranks[2], mean_ranks[3]]
})
print("\nBảng tóm tắt kết quả:")
print(results_summary.round(2))
# Kết luận
alpha = 0.05
if kruskal_p < alpha:
print(f"\nKết luận: Với p-value = {kruskal_p:.6f} < α = {alpha}") print("Bác bỏ giả thuyết H0. Có sự khác biệt có ý nghĩa thống kê về thu nhập giữa các lĩnh vực.") else: print(f"\nKết luận: Với p-value = {kruskal_p:.6f} >= α = {alpha}")
print("Không bác bỏ giả thuyết H0. Không có sự khác biệt có ý nghĩa thống kê về thu nhập giữa các lĩnh vực.")
# Lưu kết quả
results_dict = {
'kruskal_statistic': kruskal_stat,
'p_value': kruskal_p,
'effect_size': eta_squared,
'mean_ranks': mean_ranks.to_dict(),
'summary_stats': summary_stats.to_dict()
}
print("\nKiểm định Kruskal-Wallis hoàn tất!")
Tài liệu tham khảo
Để nghiên cứu sâu hơn về kiểm định Kruskal-Wallis và ứng dụng trong thực hành kinh tế lượng, độc giả có thể tham khảo các tài liệu sau:
- Kruskal, W. H. & Wallis, W. A. (1952): “Use of ranks in one-criterion variance analysis” – Journal of the American Statistical Association
- Hollander, M. & Wolfe, D. A. (2013): “Nonparametric Statistical Methods” – Wiley
- Daniel, W. W. (2017): “Biostatistics: A Foundation for Analysis in the Health Sciences” – Chapter on nonparametric tests
- IBM SPSS Statistics Documentation: Hướng dẫn chi tiết về kiểm định phi tham số
- Siegel, S. & Castellan, N. J. (1988): “Nonparametric Statistics for the Behavioral Sciences”
- Conover, W. J. (1999): “Practical Nonparametric Statistics” – Wiley