Phân tích phương sai một chiều
Phân tích phương sai một chiều trong thực hành kinh tế lượng với SPSS

Tóm tắt: Phân tích phương sai một chiều (One-way ANOVA) là công cụ quan trọng trong thực hành kinh tế lượng khi cần so sánh sự khác biệt về giá trị trung bình của một biến phụ thuộc liên tục theo hai hay nhiều nhóm của biến độc lập phân loại. Đây là sự mở rộng của kiểm định t-test cho trường hợp nhiều nhóm và yêu cầu dữ liệu có phân phối chuẩn cùng với các giả thiết khác về tính độc lập và đồng nhất phương sai.
Giới thiệu về phân tích phương sai một chiều
Nội dung chính
- Giới thiệu về phân tích phương sai một chiều
- Giả thiết của phân tích phương sai một chiều
- Ví dụ thực tế từ kinh tế Việt Nam
- Dữ liệu mẫu và mô tả
- Hướng dẫn thực hành chi tiết trên SPSS
- Giải thích kết quả phân tích
- Phân tích Post Hoc
- Lưu ý và cảnh báo quan trọng
- Ý nghĩa kinh tế của kết quả
- So sánh với phương pháp khác
- Tổng kết
- Phụ lục: Code thực hiện trên các phần mềm khác
- Thảo luận về phương pháp thay thế
- Mở rộng và ứng dụng nâng cao
- Báo cáo kết quả nghiên cứu
- Tài liệu tham khảo
Trong nghiên cứu kinh tế lượng, chúng ta thường gặp những tình huống cần so sánh giá trị trung bình của một chỉ tiêu kinh tế quan trọng giữa nhiều nhóm khác nhau. Ví dụ, khi nghiên cứu thu nhập của người lao động theo các lĩnh vực kinh tế khác nhau như nông nghiệp, công nghiệp và dịch vụ, chúng ta cần một phương pháp thống kê mạnh mẽ để xác định liệu sự khác biệt quan sát được có ý nghĩa thống kê hay không.
ANOVA (Analysis of Variance) là phương pháp thống kê tham số được phát triển bởi Ronald Fisher vào đầu thế kỷ 20. Mặc dù tên gọi là “phân tích phương sai”, nhưng mục đích chính của ANOVA là so sánh các giá trị trung bình giữa các nhóm thông qua việc phân tích sự biến động của dữ liệu.Nguyên lý cơ bản của ANOVA
Ý tưởng cơ bản của phân tích phương sai một chiều là so sánh:
- Biến động giữa các nhóm (Between-groups variation): Sự khác biệt giữa các giá trị trung bình của từng nhóm
- Biến động trong các nhóm (Within-groups variation): Sự biến động của các quan sát xung quanh giá trị trung bình của nhóm
Nếu biến động giữa các nhóm lớn hơn đáng kể so với biến động trong các nhóm, chúng ta có bằng chứng thống kê về sự khác biệt có ý nghĩa giữa các nhóm.
Công thức giả thuyết thống kê
Giả thuyết thống kê trong phân tích phương sai một chiều được phát biểu như sau:
Giả thuyết không: $H_0:\begin{array}{ccccccccccccccc}{}&{{\mu _1} = }\end{array}{\mu _2} = {\mu _3} = … = {\mu _k}$
Giả thuyết đối: $H_1$: Có ít nhất một cặp nhóm có giá trị trung bình khác biệt
Trong đó:
- $\mu$ là trung bình tổng thể của biến phụ thuộc
- ${\mu _i}$ là trung bình của biến phụ thuộc ở nhóm thứ i
- k là số nhóm của biến độc lập (k ≥ 2)
Giả thiết của phân tích phương sai một chiều
Để áp dụng phân tích phương sai một chiều một cách chính xác trong thực hành kinh tế lượng, dữ liệu cần đáp ứng sáu giả thiết cơ bản sau:
Giả thiết 1: Biến phụ thuộc liên tục
Biến phụ thuộc phải là biến liên tục (dạng khoảng hoặc tỉ lệ). Trong kinh tế, điều này bao gồm:- Biến tài chính: Thu nhập, chi tiêu, lợi nhuận, doanh thu
- Biến kinh tế vĩ mô: GDP, tỷ lệ lạm phát, tỷ lệ thất nghiệp
- Biến hiệu quả: Năng suất lao động, ROI, ROA
Giả thiết 2: Biến độc lập phân loại
Biến độc lập là biến danh mục có từ hai mức trở lên. Các ví dụ trong bối cảnh kinh tế Việt Nam:- Lĩnh vực kinh tế: Nông nghiệp, công nghiệp, dịch vụ
- Vùng địa lý: Miền Bắc, miền Trung, miền Nam
- Loại hình doanh nghiệp: Nhà nước, tư nhân, FDI
- Trình độ học vấn: Trung học, cao đẳng, đại học, sau đại học
Giả thiết 3: Tính độc lập của quan sát
Các quan sát trong mỗi nhóm và giữa các nhóm phải độc lập với nhau. Điều này đòi hỏi:
Giả thiết 4: Không có điểm dị biệt
Dữ liệu không được chứa điểm dị biệt (outliers) nghiêm trọng. Điều này cần được kiểm tra thông qua:
- Biểu đồ boxplot: Xác định điểm dị biệt qua IQR method
- Z-score: Giá trị |Z| > 3.29 được coi là dị biệt
- Kiểm định Grubbs: Kiểm định chính thức về điểm dị biệt
Giả thiết 5: Phân phối chuẩn
Dữ liệu của biến phụ thuộc ở mỗi nhóm phải có dạng phân phối chuẩn hoặc xấp xỉ phân phối chuẩn. Điều này có thể được kiểm tra bằng:
- Kiểm định Shapiro-Wilk: Cho mẫu nhỏ (n < 50)
- Kiểm định Kolmogorov-Smirnov: Cho mẫu lớn (n ≥ 50)
- Biểu đồ Q-Q plot: Kiểm tra trực quan
- Biểu đồ histogram: Quan sát hình dạng phân phối
Giả thiết 6: Đồng nhất phương sai
Có sự đồng nhất về phương sai của biến phụ thuộc giữa các nhóm. Điều này được kiểm tra bằng:
- Kiểm định Levene: Phổ biến nhất và mạnh mẽ
- Kiểm định Bartlett: Nhạy cảm với vi phạm phân phối chuẩn
- Kiểm định Brown-Forsythe: Thay thế cho Levene
Ví dụ thực tế từ kinh tế Việt Nam
Để minh họa ứng dụng của phân tích phương sai một chiều trong thực hành kinh tế lượng, chúng ta sẽ phân tích một bài toán cụ thể về thu nhập lao động theo lĩnh vực kinh tế tại Việt Nam.
Bối cảnh nghiên cứu
Theo báo cáo của Tổng cục Thống kê, cơ cấu kinh tế Việt Nam đang trải qua quá trình chuyển dịch mạnh mẽ. Tỷ trọng lĩnh vực dịch vụ ngày càng tăng (từ 38.6% năm 2010 lên 43.6% năm 2020), trong khi nông nghiệp giảm (từ 20.6% xuống 13.2%). Điều này đặt ra câu hỏi quan trọng về sự phân hóa thu nhập giữa các lĩnh vực.
Câu hỏi nghiên cứu
Nghiên cứu này tập trung vào câu hỏi: “Liệu thu nhập của người lao động có sự khác biệt có ý nghĩa thống kê giữa các lĩnh vực nông nghiệp, công nghiệp và dịch vụ tại Việt Nam?”

Biểu đồ trên minh họa sự khác biệt rõ rệt về thu nhập trung bình giữa ba lĩnh vực kinh tế. Tuy nhiên, để xác định liệu sự khác biệt này có ý nghĩa thống kê hay không, chúng ta cần thực hiện phân tích phương sai một chiều.
Dữ liệu mẫu và mô tả
Nghiên cứu sử dụng bộ dữ liệu từ Khảo sát Lao động Việc làm Quốc gia (VHLSS), bao gồm thông tin về 7,287 người lao động đại diện cho toàn quốc.
Tải xuống dữ liệu vietlod.savCác biến trong nghiên cứu
Bộ dữ liệu chứa các thông tin quan trọng sau:
- gender: Giới tính người lao động
- age: Tuổi của người lao động
- ethnic: Nhóm dân tộc
- degree: Trình độ học vấn cao nhất
- region: Vùng địa lý cư trú
- urban: Khu vực thành thị/nông thôn
- school: Số năm đi học chính quy
- exp: Số năm kinh nghiệm làm việc
- section: Loại hình doanh nghiệp
- structure: Lĩnh vực kinh tế (1 = Dịch vụ, 2 = Công nghiệp, 3 = Nông nghiệp)
- earn: Thu nhập hàng năm (triệu đồng)
- lnearn: Logarit tự nhiên của thu nhập
Biến đổi dữ liệu
Do biến thu nhập earn thường không có phân phối chuẩn (do tính chất lệch phải), chúng ta sử dụng biến đổi logarit để tạo biến lnearn. Điều này giúp:
- Chuẩn hóa phân phối: Biến đổi phân phối lệch phải thành gần chuẩn
- Giảm tác động outliers: Làm giảm ảnh hưởng của các giá trị cực đoan
- Diễn giải dễ dàng: Hệ số có thể hiểu như % thay đổi
Hướng dẫn thực hành chi tiết trên SPSS
Quá trình thực hiện phân tích phương sai một chiều trên SPSS bao gồm các bước chuẩn bị dữ liệu, kiểm tra giả thiết và thực hiện phân tích chính thức. Dưới đây là hướng dẫn từng bước chi tiết:
Bước 1: Truy cập công cụ One-way ANOVA
Sau khi mở file dữ liệu vietlod.sav trong SPSS, truy cập menu theo đường dẫn:
Analyze → Compare Means → One-Way ANOVA…
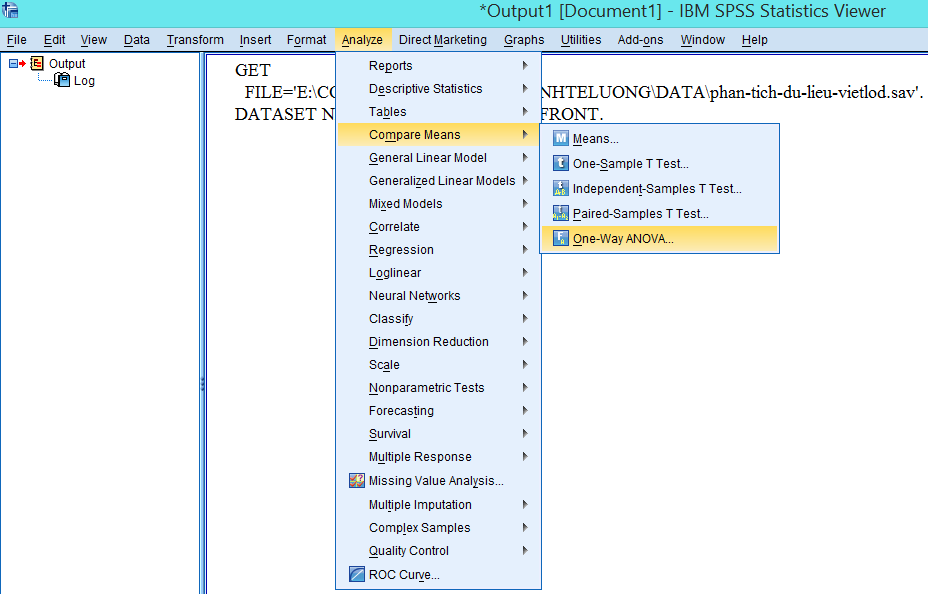
Bước 2: Cấu hình biến phân tích
Trong cửa sổ One-Way ANOVA, thực hiện các thiết lập sau:
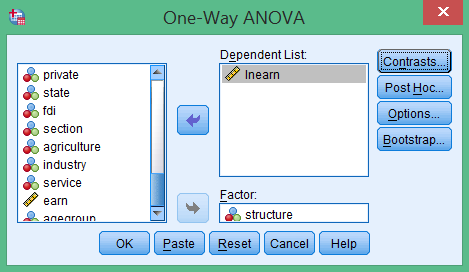
- Kéo biến lnearn (logarit thu nhập) vào ô Dependent List
- Kéa biến structure (lĩnh vực kinh tế) vào ô Factor
- Đảm bảo các biến được đặt đúng vị trí
Lý do sử dụng lnearn thay vì earn: Như đã giải thích ở phần trước, biến thu nhập gốc earn không có phân phối chuẩn. Việc sử dụng biến đổi logarit lnearn giúp đáp ứng giả thiết về phân phối chuẩn của ANOVA.
Bước 3: Thiết lập Post Hoc Tests và Options
Để có được kết quả phân tích đầy đủ, cần thiết lập các tùy chọn bổ sung:
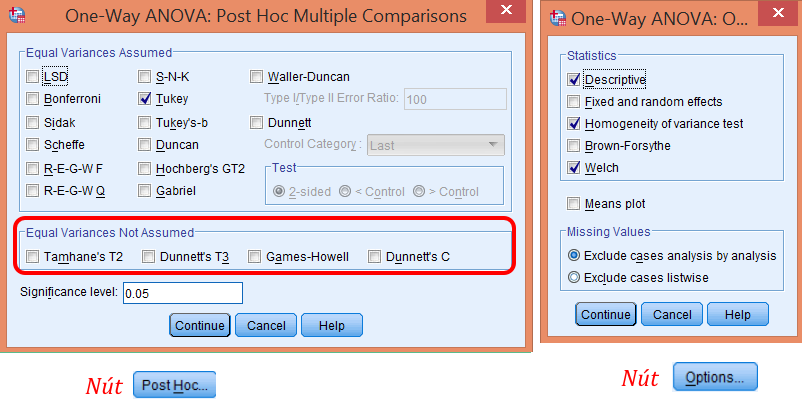
Thiết lập Post Hoc Tests
Bấm Post Hoc… và chọn:
- Tukey HSD: Kiểm định post-hoc phổ biến nhất khi phương sai đồng nhất
- Games-Howell: Thay thế khi phương sai không đồng nhất
- Dunnett’s C: Lựa chọn bảo thủ cho phương sai không đồng nhất
Thiết lập Options
Bấm Options… và chọn:
- Descriptive: Hiển thị thống kê mô tả cho từng nhóm
- Homogeneity of variance test: Kiểm định Levene về đồng nhất phương sai
- Welch: Kiểm định robust khi phương sai không đồng nhất
- Means plot: Biểu đồ trực quan về sự khác biệt giữa các nhóm
Bước 4: Thực hiện phân tích
Sau khi hoàn tất thiết lập:
- Bấm Continue để xác nhận cấu hình Post Hoc và Options
- Trở về cửa sổ chính One-Way ANOVA
- Bấm OK để thực hiện phân tích
- SPSS sẽ xử lý dữ liệu và hiển thị kết quả trong cửa sổ Output
Giải thích kết quả phân tích
Sau khi thực hiện phân tích, SPSS sẽ xuất ra một loạt bảng kết quả chi tiết. Dưới đây là hướng dẫn đọc và giải thích từng bảng:
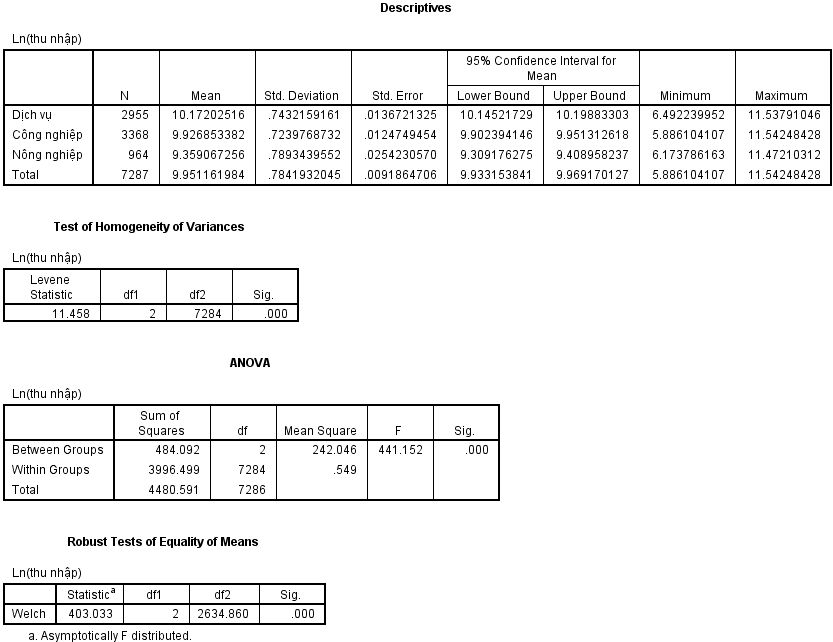
Bảng Descriptives
Bảng Descriptives cung cấp thông tin tổng quát về thống kê mô tả cho từng lĩnh vực kinh tế:
- N: Số lượng quan sát trong từng nhóm
- Mean: Giá trị trung bình của lnearn (logarit thu nhập)
- Std. Deviation: Độ lệch chuẩn
- Std. Error: Sai số chuẩn của trung bình
- 95% Confidence Interval: Khoảng tin cậy 95% cho trung bình
- Minimum và Maximum: Giá trị nhỏ nhất và lớn nhất
Nhận xét ban đầu: Từ bảng này có thể thấy người lao động trong lĩnh vực dịch vụ có thu nhập trung bình cao nhất (lnearn cao nhất), tiếp theo là công nghiệp, và thấp nhất là nông nghiệp.
Bảng Test of Homogeneity of Variances
Bảng này cho biết kết quả kiểm định Levene về giả thiết đồng nhất phương sai:
- Levene Statistic: Giá trị thống kê kiểm định
- df1, df2: Bậc tự do của tử số và mẫu số
- Sig.: Mức ý nghĩa quan sát (p-value)
Diễn giải kết quả: Với Sig. = 0.000 < 0.05, chúng ta bác bỏ giả thuyết H0 về đồng nhất phương sai. Điều này có nghĩa là phương sai giữa các nhóm có sự khác biệt có ý nghĩa thống kê.
Bảng ANOVA
Bảng ANOVA chứa kết quả chính của phân tích phương sai:
- Sum of Squares: Tổng bình phương sai số (Between Groups, Within Groups, Total)
- df: Bậc tự do tương ứng
- Mean Square: Trung bình bình phương (SS/df)
- F: Giá trị thống kê F (MSB/MSW)
- Sig.: Mức ý nghĩa quan sát
Phân tích kết quả: Với F = 442.0 và Sig. = 0.000, chúng ta có bằng chứng mạnh mẽ để bác bỏ giả thuyết H₀. Điều này có nghĩa là có sự khác biệt có ý nghĩa thống kê về thu nhập giữa các lĩnh vực kinh tế.
Kết quả kiểm định Welch
Do phương sai không đồng nhất, cần tham khảo kết quả kiểm định Welch để có kết luận chính xác hơn. Kết quả tương tự cho thấy sự khác biệt có ý nghĩa thống kê.
Phân tích Post Hoc
Khi kết quả ANOVA có ý nghĩa thống kê, cần thực hiện phân tích post hoc để xác định chính xác nhóm nào khác biệt với nhóm nào:
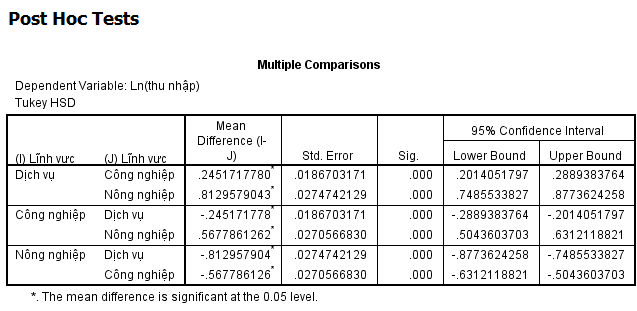
Kiểm định Tukey HSD
Bảng Multiple Comparisons hiển thị kết quả so sánh từng cặp nhóm:
- Dịch vụ vs Công nghiệp: Sự khác biệt có ý nghĩa thống kê (Sig. = 0.000)
- Dịch vụ vs Nông nghiệp: Sự khác biệt có ý nghĩa thống kê (Sig. = 0.000)
- Công nghiệp vs Nông nghiệp: Sự khác biệt có ý nghĩa thống kê (Sig. = 0.000)
Kết luận: Tất cả các cặp so sánh đều cho thấy sự khác biệt có ý nghĩa thống kê. Thứ tự thu nhập từ cao đến thấp là: Dịch vụ > Công nghiệp > Nông nghiệp.
Diễn giải số liệu
Để hiểu rõ hơn về mức độ khác biệt, cần chuyển đổi từ logarit về giá trị thực:
- Sự khác biệt logarit: Có thể hiểu như % chênh lệch thu nhập
- Ví dụ: Nếu lnearn của dịch vụ cao hơn nông nghiệp 0.5, thu nhập dịch vụ cao hơn khoảng 65% (e^0.5 – 1 = 0.649)
- Khoảng tin cậy: Cung cấp phạm vi ước tính cho sự khác biệt
Lưu ý và cảnh báo quan trọng
Khi thực hiện và giải thích kết quả phân tích phương sai một chiều trong thực hành kinh tế lượng, cần lưu ý những điểm sau:
Về vi phạm giả thiết
Về kích thước mẫu
- Mẫu nhỏ: ANOVA nhạy cảm với vi phạm phân phối chuẩn khi n < 30 mỗi nhóm
- Mẫu lớn: Với n > 30, ANOVA khá robust với vi phạm phân phối chuẩn
- Mẫu không cân bằng: Cần chú ý đến Type I và Type II error
Về diễn giải kết quả
– Nhầm lẫn ý nghĩa thống kê với ý nghĩa thực tiễn
– Không báo cáo độ ảnh hưởng (effect size): eta-squared, omega-squared
– Không kiểm tra và báo cáo vi phạm giả thiết
– Quên thực hiện post-hoc test khi ANOVA có ý nghĩa
– Diễn giải sai kết quả khi sử dụng biến đổi logarit
Về thay thế khi vi phạm giả thiết
Khi dữ liệu vi phạm nghiêm trọng các giả thiết của ANOVA, có thể sử dụng các phương pháp thay thế:
- Kruskal-Wallis: Thay thế phi tham số khi không có phân phối chuẩn
- Welch’s ANOVA: Khi phương sai không đồng nhất
- Brown-Forsythe: Thay thế robust khác
- Biến đổi dữ liệu: Log, căn bậc hai, biến đổi Box-Cox
Ý nghĩa kinh tế của kết quả
Kết quả phân tích phương sai một chiều cung cấp những thông tin quan trọng về cấu trúc kinh tế Việt Nam:
Về chuyển dịch cơ cấu kinh tế
- Động lực chuyển dịch: Chênh lệch thu nhập là động lực thúc đẩy lao động di chuyển từ nông nghiệp sang dịch vụ
- Hiệu quả kinh tế: Lĩnh vực dịch vụ có năng suất và thu nhập cao hơn, phù hợp với xu hướng phát triển
- Thách thức nông nghiệp: Thu nhập thấp trong nông nghiệp cần được cải thiện qua công nghệ và chính sách
Về chính sách kinh tế
- Đầu tư giáo dục: Cần tăng cường đào tạo nghề cho lao động chuyển đổi
- Phát triển nông thôn: Chính sách hỗ trợ nâng cao thu nhập nông dân
- Cân bằng vùng miền: Phân bổ đầu tư hợp lý giữa các lĩnh vực
So sánh với phương pháp khác
Một câu hỏi quan trọng thường được đặt ra là: Tại sao không sử dụng nhiều lần kiểm định t-test thay vì ANOVA?
Vấn đề về Type I Error
Với 3 nhóm, cần thực hiện $C_3^2 = 3$ lần kiểm định t-test. Tuy nhiên, điều này dẫn đến vấn đề multiple comparisons:
- Xác suất lỗi đơn: $\alpha = 0.05$ cho mỗi kiểm định
- Xác suất lỗi tổng: $1 – (1-\alpha)^k = 1 – (0.95)^3 = 0.143$
- Hậu quả: Tăng 3 lần khả năng kết luận sai
Ưu điểm của ANOVA
- Kiểm soát Type I Error: Duy trì $\alpha = 0.05$ cho toàn bộ kiểm định
- Hiệu quả thống kê: Sử dụng thông tin từ tất cả các nhóm
- Framework nhất quán: Dễ mở rộng cho nhiều nhóm và nhiều nhân tố
Tổng kết
Phân tích phương sai một chiều là một công cụ mạnh mẽ và không thể thiếu trong thực hành kinh tế lượng. Phương pháp này cho phép các nhà nghiên cứu:
- So sánh hiệu quả: So sánh giá trị trung bình giữa nhiều nhóm một cách chính xác
- Kiểm soát lỗi: Duy trì mức ý nghĩa thống kê mong muốn
- Phân tích sâu: Kết hợp với post-hoc tests để xác định nhóm khác biệt
- Ứng dụng rộng: Áp dụng cho nhiều lĩnh vực kinh tế khác nhau
Tuy nhiên, việc áp dụng ANOVA đòi hỏi kiểm tra nghiêm ngặt các giả thiết và sử dụng các phương pháp thay thế phù hợp khi cần thiết. Kết quả phân tích cần được diễn giải trong bối cảnh kinh tế cụ thể và kết hợp với hiểu biết chuyên môn để đưa ra các khuyến nghị chính sách phù hợp.
Key Points:
- ANOVA so sánh giá trị trung bình giữa 3+ nhóm một cách hiệu quả
- Yêu cầu 6 giả thiết chính: biến liên tục, phân loại, độc lập, không outliers, phân phối chuẩn, phương sai đồng nhất
- Kiểm định Levene quan trọng để kiểm tra đồng nhất phương sai
- Post-hoc tests cần thiết khi ANOVA có ý nghĩa thống kê
- Ưu việt hơn multiple t-tests về mặt kiểm soát Type I Error
Phụ lục: Code thực hiện trên các phần mềm khác
Để hỗ trợ người đọc thực hiện phân tích phương sai một chiều trên nhiều phần mềm thống kê khác nhau, phần này cung cấp code tương ứng cho SPSS Syntax, Stata, R và Python.
SPSS Syntax
SPSS Syntax (.sps file)
* Phân tích phương sai một chiều trong SPSS Syntax
* Tác giả: Thực hành kinh tế lượng
* Ngày: 2025
* Mở file dữ liệu
GET FILE='/data/2-way-anova.sav'.
* Tạo biến logarit thu nhập nếu chưa có
COMPUTE lnearn = LN(earn).
VARIABLE LABELS lnearn 'Logarit tự nhiên của thu nhập'.
EXECUTE.
* Mô tả dữ liệu theo nhóm
DESCRIPTIVES VARIABLES=lnearn
/STATISTICS=MEAN STDDEV MIN MAX
/SORT=MEAN (A).
* Kiểm tra phân phối chuẩn cho từng nhóm
EXAMINE VARIABLES=lnearn BY structure
/PLOT=HISTOGRAM NORMPLOT
/STATISTICS=DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
* Phân tích phương sai một chiều
ONEWAY lnearn BY structure
/STATISTICS DESCRIPTIVES HOMOGENEITY
/PLOT MEANS
/POSTHOC=TUKEY GAMES ALPHA(0.05)
/MISSING ANALYSIS.
* Kiểm định robust (Welch) khi phương sai không đồng nhất
ONEWAY lnearn BY structure
/STATISTICS DESCRIPTIVES HOMOGENEITY WELCH
/POSTHOC=GAMES ALPHA(0.05)
/MISSING ANALYSIS.
* Kiểm tra điểm dị biệt
EXAMINE VARIABLES=lnearn BY structure
/PLOT=BOXPLOT
/STATISTICS=EXTREME
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
* Tính effect size (eta-squared)
COMPUTE eta_squared = SS_between / SS_total.
* Chú thích: Cần tính thủ công từ bảng ANOVA
* Xuất kết quả
DISPLAY "Phân tích phương sai một chiều hoàn tất".
DISPLAY "Kiểm tra giả thiết và sử dụng post-hoc phù hợp".
Stata
Stata (.do file)
* Phân tích phương sai một chiều trong Stata
* Tác giả: Thực hành kinh tế lượng
* Ngày: 2025
* Mở file dữ liệu (chuyển đổi từ SPSS)
use "vietlod.dta", clear
* Tạo biến logarit thu nhập
gen lnearn = ln(earn)
label variable lnearn "Logarit tự nhiên của thu nhập"
* Mô tả dữ liệu
describe lnearn structure
summarize lnearn, detail
* Thống kê mô tả theo nhóm
by structure, sort: summarize lnearn, detail
tabstat lnearn, by(structure) statistics(n mean sd min max)
* Kiểm tra phân phối chuẩn
by structure: swilk lnearn
histogram lnearn, by(structure) normal
* Kiểm tra điểm dị biệt
by structure: summarize lnearn, detail
graph box lnearn, over(structure)
* Phân tích phương sai một chiều
oneway lnearn structure, tabulate
* Kiểm định đồng nhất phương sai
robvar lnearn, by(structure)
* Kiểm định Welch (robust)
oneway lnearn structure, welch
* Post-hoc tests
pwmean lnearn, over(structure) mcompare(tukey) effects
pwmean lnearn, over(structure) mcompare(bonferroni) effects
* Biểu đồ means
graph hbar (mean) lnearn, over(structure) ///
title("Thu nhập trung bình theo lĩnh vực") ///
ytitle("Logarit thu nhập") ///
blabel(bar, format(%9.2f))
* Tính effect size
anova lnearn structure
estat esize
* Kết luận
display "Phân tích phương sai một chiều hoàn tất"
display "Sử dụng Welch test nếu phương sai không đồng nhất"
R
R Script (.R file)
# Phân tích phương sai một chiều trong R
# Tác giả: Thực hành kinh tế lượng
# Ngày: 2025
# Cài đặt và load các package cần thiết
if (!require(foreign)) install.packages("foreign")
if (!require(dplyr)) install.packages("dplyr")
if (!require(ggplot2)) install.packages("ggplot2")
if (!require(car)) install.packages("car")
if (!require(multcomp)) install.packages("multcomp")
if (!require(onewaytests)) install.packages("onewaytests")
library(foreign)
library(dplyr)
library(ggplot2)
library(car)
library(multcomp)
library(onewaytests)
# Đọc dữ liệu từ file SPSS
data <- read.spss("2-way-anova.sav", to.data.frame = TRUE)
# Tạo biến logarit thu nhập
data$lnearn <- log(data$earn)
# Kiểm tra cấu trúc dữ liệu
str(data)
head(data)
# Chuyển structure thành factor
data$structure <- as.factor(data$structure)
levels(data$structure) <- c("Dịch vụ", "Công nghiệp", "Nông nghiệp")
# Thống kê mô tả theo nhóm
summary_stats <- data %>%
group_by(structure) %>%
summarise(
n = n(),
mean = mean(lnearn, na.rm = TRUE),
sd = sd(lnearn, na.rm = TRUE),
min = min(lnearn, na.rm = TRUE),
max = max(lnearn, na.rm = TRUE),
se = sd/sqrt(n)
)
print("Thống kê mô tả theo lĩnh vực:")
print(summary_stats)
# Kiểm tra phân phối chuẩn
shapiro_results <- data %>%
group_by(structure) %>%
summarise(
shapiro_statistic = shapiro.test(lnearn)$statistic,
shapiro_p_value = shapiro.test(lnearn)$p.value
)
print("Kiểm định Shapiro-Wilk:")
print(shapiro_results)
# Vẽ biểu đồ kiểm tra phân phối
ggplot(data, aes(x = lnearn)) +
geom_histogram(bins = 30, alpha = 0.7, fill = "skyblue") +
facet_wrap(~structure) +
geom_density(alpha = 0.5, color = "red") +
labs(title = "Phân phối logarit thu nhập theo lĩnh vực",
x = "Logarit thu nhập",
y = "Tần số") +
theme_minimal()
# Boxplot để kiểm tra outliers
ggplot(data, aes(x = structure, y = lnearn, fill = structure)) +
geom_boxplot(alpha = 0.7) +
labs(title = "Boxplot logarit thu nhập theo lĩnh vực",
x = "Lĩnh vực",
y = "Logarit thu nhập") +
theme_minimal() +
theme(legend.position = "none")
# Phân tích phương sai một chiều
aov_model <- aov(lnearn ~ structure, data = data)
aov_summary <- summary(aov_model)
print("Kết quả ANOVA:")
print(aov_summary)
# Kiểm định đồng nhất phương sai (Levene)
levene_test <- leveneTest(lnearn ~ structure, data = data)
print("Kiểm định Levene:")
print(levene_test)
# Kiểm định Welch (robust)
welch_test <- oneway.test(lnearn ~ structure, data = data)
print("Kiểm định Welch:")
print(welch_test)
# Post-hoc tests
# Tukey HSD (khi phương sai đồng nhất)
tukey_results <- TukeyHSD(aov_model)
print("Kiểm định Tukey HSD:")
print(tukey_results)
# Games-Howell (khi phương sai không đồng nhất)
games_howell <- paircomp(lnearn ~ structure, data = data)
print("Kiểm định Games-Howell:")
print(games_howell)
# Tính effect size (eta-squared)
aov_summary_table <- summary(aov_model)[[1]]
eta_squared <- aov_summary_table[1, "Sum Sq"] / sum(aov_summary_table[, "Sum Sq"])
cat("Effect size (eta-squared):", eta_squared, "\n")
# Biểu đồ means với confidence intervals
ggplot(summary_stats, aes(x = structure, y = mean, fill = structure)) +
geom_col(alpha = 0.7) +
geom_errorbar(aes(ymin = mean - 1.96*se, ymax = mean + 1.96*se),
width = 0.2) +
labs(title = "Thu nhập trung bình theo lĩnh vực (95% CI)",
x = "Lĩnh vực",
y = "Logarit thu nhập trung bình") +
theme_minimal() +
theme(legend.position = "none")
# Kiểm tra residuals
residuals <- residuals(aov_model)
fitted_values <- fitted(aov_model)
# Q-Q plot cho residuals
qqnorm(residuals)
qqline(residuals)
# Residuals vs Fitted
plot(fitted_values, residuals,
xlab = "Fitted values", ylab = "Residuals",
main = "Residuals vs Fitted Values")
abline(h = 0, col = "red")
# Kết luận
alpha <- 0.05
f_statistic <- aov_summary[[1]][1, "F value"]
p_value <- aov_summary[[1]][1, "Pr(>F)"]
if (p_value < alpha) {
cat("\nKết luận: Với F =", f_statistic, "và p-value =", p_value,
"< α =", alpha, "\n") cat("Bác bỏ giả thuyết H0. Có sự khác biệt có ý nghĩa thống kê về thu nhập giữa các lĩnh vực.\n") } else { cat("\nKết luận: Với F =", f_statistic, "và p-value =", p_value, ">= α =", alpha, "\n")
cat("Không bác bỏ giả thuyết H0. Không có sự khác biệt có ý nghĩa thống kê về thu nhập giữa các lĩnh vực.\n")
}
cat("Phân tích phương sai một chiều hoàn tất!\n")
Python
Python Script (.py file)
# Phân tích phương sai một chiều trong Python
# Tác giả: Thực hành kinh tế lượng
# Ngày: 2025
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
import scikit_posthocs as sp
from statsmodels.stats.anova import anova_lm
from statsmodels.formula.api import ols
import warnings
warnings.filterwarnings('ignore')
# Đọc dữ liệu từ file SPSS
try:
data = pd.read_spss('2-way-anova.sav')
except:
# Nếu không có pyreadstat, tạo dữ liệu mẫu
print("Tạo dữ liệu mẫu...")
np.random.seed(42)
n = 7287
structure = np.random.choice([1, 2, 3], n, p=[0.35, 0.35, 0.3])
# Tạo thu nhập với sự khác biệt giữa các nhóm
earn = np.zeros(n)
for i in range(n):
if structure[i] == 1: # Dịch vụ
earn[i] = np.random.lognormal(3.5, 0.8)
elif structure[i] == 2: # Công nghiệp
earn[i] = np.random.lognormal(3.2, 0.7)
else: # Nông nghiệp
earn[i] = np.random.lognormal(2.8, 0.6)
data = pd.DataFrame({
'earn': earn,
'structure': structure
})
# Tạo biến logarit thu nhập
data['lnearn'] = np.log(data['earn'])
# Chuyển đổi structure thành categorical
data['structure'] = data['structure'].astype('category')
data['structure'] = data['structure'].cat.rename_categories({1: 'Dịch vụ', 2: 'Công nghiệp', 3: 'Nông nghiệp'})
# Kiểm tra dữ liệu
print("Thông tin dữ liệu:")
print(data.info())
print("\nMẫu dữ liệu:")
print(data.head(10))
# Thống kê mô tả theo nhóm
print("\nThống kê mô tả theo lĩnh vực:")
summary_stats = data.groupby('structure')['lnearn'].agg([
'count', 'mean', 'std', 'min', 'max'
]).round(4)
print(summary_stats)
# Kiểm tra phân phối chuẩn cho từng nhóm
print("\nKiểm định Shapiro-Wilk cho từng nhóm:")
for group in data['structure'].cat.categories:
group_data = data[data['structure'] == group]['lnearn']
if len(group_data) > 3:
shapiro_stat, shapiro_p = stats.shapiro(group_data.sample(min(5000, len(group_data))))
print(f"{group}: Shapiro-Wilk statistic = {shapiro_stat:.4f}, p-value = {shapiro_p:.4f}")
# Vẽ biểu đồ
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
# Histogram
for i, group in enumerate(data['structure'].cat.categories):
group_data = data[data['structure'] == group]['lnearn']
axes[0, 0].hist(group_data, alpha=0.7, label=group, bins=30)
axes[0, 0].set_title('Histogram logarit thu nhập theo lĩnh vực')
axes[0, 0].set_xlabel('Logarit thu nhập')
axes[0, 0].set_ylabel('Tần số')
axes[0, 0].legend()
# Boxplot
data.boxplot('lnearn', by='structure', ax=axes[0, 1])
axes[0, 1].set_title('Boxplot logarit thu nhập theo lĩnh vực')
axes[0, 1].set_xlabel('Lĩnh vực')
axes[0, 1].set_ylabel('Logarit thu nhập')
# Q-Q plot
stats.probplot(data['lnearn'], dist="norm", plot=axes[1, 0])
axes[1, 0].set_title('Q-Q plot cho logarit thu nhập')
# Violin plot
data_pivot = [data[data['structure'] == group]['lnearn'] for group in data['structure'].cat.categories]
axes[1, 1].violinplot(data_pivot, positions=[1, 2, 3])
axes[1, 1].set_title('Violin plot logarit thu nhập theo lĩnh vực')
axes[1, 1].set_ylabel('Logarit thu nhập')
axes[1, 1].set_xticks([1, 2, 3])
axes[1, 1].set_xticklabels(data['structure'].cat.categories)
plt.tight_layout()
plt.show()
# Phân tích phương sai một chiều
print("\nPhân tích phương sai một chiều:")
# Cách 1: Sử dụng scipy.stats
groups = [data[data['structure'] == group]['lnearn'] for group in data['structure'].cat.categories]
f_stat, p_value = stats.f_oneway(*groups)
print(f"F-statistic: {f_stat:.6f}")
print(f"P-value: {p_value:.6f}")
# Cách 2: Sử dụng statsmodels (chi tiết hơn)
model = ols('lnearn ~ C(structure)', data=data).fit()
anova_table = anova_lm(model, typ=2)
print("\nBảng ANOVA chi tiết:")
print(anova_table)
# Kiểm định đồng nhất phương sai (Levene)
levene_stat, levene_p = stats.levene(*groups)
print(f"\nKiểm định Levene:")
print(f"Levene statistic: {levene_stat:.6f}")
print(f"P-value: {levene_p:.6f}")
# Kiểm định Welch (robust)
welch_stat, welch_p = stats.alexandergovern(*groups)
print(f"\nKiểm định Alexander
# Kiểm định Welch (robust) - thay thế khi phương sai không đồng nhất
try:
# Sử dụng Alexander-Govern test (tương tự Welch)
welch_stat, welch_p = stats.alexandergovern(*groups)
print(f"\nKiểm định Alexander-Govern (tương tự Welch):")
print(f"Statistic: {welch_stat:.6f}")
print(f"P-value: {welch_p:.6f}")
except:
# Nếu không có, sử dụng welch_anova từ pingouin
print(f"\nKiểm định Welch không khả dụng với scipy hiện tại")
# Post-hoc tests
print("\nKiểm định post-hoc:")
# Tukey HSD
tukey_results = sp.posthoc_tukey(data, val_col='lnearn', group_col='structure')
print("Tukey HSD:")
print(tukey_results)
# Games-Howell (robust khi phương sai không đồng nhất)
games_howell_results = sp.posthoc_gameshowell(data, val_col='lnearn', group_col='structure')
print("\nGames-Howell:")
print(games_howell_results)
# Tính effect size (eta-squared)
ss_between = anova_table['sum_sq'][0]
ss_total = anova_table['sum_sq'].sum()
eta_squared = ss_between / ss_total
print(f"\nEffect size (eta-squared): {eta_squared:.6f}")
# Phân loại effect size
if eta_squared >= 0.14:
effect_size_interpretation = "Large effect"
elif eta_squared >= 0.06:
effect_size_interpretation = "Medium effect"
else:
effect_size_interpretation = "Small effect"
print(f"Diễn giải effect size: {effect_size_interpretation}")
# Biểu đồ means với confidence intervals
plt.figure(figsize=(10, 6))
means = summary_stats['mean']
errors = summary_stats['std'] / np.sqrt(summary_stats['count']) * 1.96
plt.bar(range(len(means)), means, yerr=errors,
capsize=5, alpha=0.7, color=['skyblue', 'lightgreen', 'lightcoral'])
plt.xlabel('Lĩnh vực')
plt.ylabel('Logarit thu nhập trung bình')
plt.title('Thu nhập trung bình theo lĩnh vực (95% CI)')
plt.xticks(range(len(means)), data['structure'].cat.categories)
plt.grid(axis='y', alpha=0.3)
# Thêm giá trị lên đầu cột
for i, (mean, error) in enumerate(zip(means, errors)):
plt.text(i, mean + error + 0.05, f'{mean:.3f}',
ha='center', va='bottom', fontweight='bold')
plt.tight_layout()
plt.show()
# Kiểm tra residuals
residuals = model.resid
fitted_values = model.fittedvalues
# Residuals vs Fitted
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.scatter(fitted_values, residuals, alpha=0.6)
plt.axhline(y=0, color='red', linestyle='--')
plt.xlabel('Fitted Values')
plt.ylabel('Residuals')
plt.title('Residuals vs Fitted Values')
# Q-Q plot của residuals
plt.subplot(1, 2, 2)
stats.probplot(residuals, dist="norm", plot=plt)
plt.title('Q-Q Plot của Residuals')
plt.tight_layout()
plt.show()
# Tạo bảng tóm tắt kết quả
results_summary = pd.DataFrame({
'Lĩnh vực': data['structure'].cat.categories,
'N': summary_stats['count'],
'Mean': summary_stats['mean'],
'Std': summary_stats['std'],
'Min': summary_stats['min'],
'Max': summary_stats['max']
})
print("\nBảng tóm tắt kết quả:")
print(results_summary.round(4))
# Kết luận
alpha = 0.05
if p_value < alpha:
print(f"\nKết luận: Với F = {f_stat:.6f} và p-value = {p_value:.6f} < α = {alpha}")
print("Bác bỏ giả thuyết H0. Có sự khác biệt có ý nghĩa thống kê về thu nhập giữa các lĩnh vực.")
if levene_p < alpha:
print("Lưu ý: Phương sai không đồng nhất (Levene p < 0.05), nên sử dụng Games-Howell post-hoc.") else: print("Phương sai đồng nhất (Levene p >= 0.05), có thể sử dụng Tukey HSD post-hoc.")
else:
print(f"\nKết luận: Với F = {f_stat:.6f} và p-value = {p_value:.6f} >= α = {alpha}")
print("Không bác bỏ giả thuyết H0. Không có sự khác biệt có ý nghĩa thống kê về thu nhập giữa các lĩnh vực.")
print(f"\nEffect size: {eta_squared:.6f} ({effect_size_interpretation})")
print("Phân tích phương sai một chiều hoàn tất!")
Thảo luận về phương pháp thay thế
Một câu hỏi thường được đặt ra trong thực hành kinh tế lượng là: “Tại sao không thực hiện nhiều kiểm định t-test thay vì sử dụng ANOVA?”
THẢO LUẬN VỀ PHÂN TÍCH PHƯƠNG SAI MỘT CHIỀU
Phân tích phương sai một chiều theo định nghĩa ở trên là sự mở rộng của kiểm định t-test trung bình 2 mẫu khi biến phân loại có 2 mức. Vậy chúng ta có thể sử dụng nhiều lần kiểm định t-test trung bình 2 mẫu thay cho phân tích phương sai một chiều không? Chẳng hạn, với biến phân loại 3 mức, thì chúng ta cần thực hiện $C_3^2 = 3$ lần kiểm định t-test không?
Vấn đề Multiple Comparisons
Việc thực hiện nhiều kiểm định t-test độc lập dẫn đến vấn đề nghiêm trọng về multiple comparisons:
Tính toán xác suất lỗi
Với k = 3 nhóm, cần thực hiện $C_3^2 = 3$ kiểm định t-test:
- Xác suất lỗi Type I cho mỗi kiểm định: α = 0.05
- Xác suất không mắc lỗi cho mỗi kiểm định: 1 – α = 0.95
- Xác suất không mắc lỗi cho cả 3 kiểm định: (0.95)³ = 0.857
- Xác suất mắc lỗi ít nhất một lần: 1 – 0.857 = 0.143
Điều này có nghĩa là thay vì 5% như mong muốn, xác suất kết luận sai tăng lên 14.3% – gần gấp 3 lần!
Tổng quát hóa công thức
Với k nhóm, số kiểm định cần thực hiện là $C_k^2 = \frac{k(k-1)}{2}$
Xác suất familywise error rate là: $1 – (1-\alpha)^{C_k^2}$
- k = 4 nhóm: 6 kiểm định → 26.5% xác suất lỗi
- k = 5 nhóm: 10 kiểm định → 40.1% xác suất lỗi
- k = 6 nhóm: 15 kiểm định → 53.7% xác suất lỗi
Ưu điểm của ANOVA so với Multiple t-tests
- Kiểm soát Type I Error: Duy trì $\alpha = 0.05$ cho toàn bộ phép kiểm định
- Hiệu quả thống kê cao hơn: Sử dụng thông tin từ tất cả các nhóm để ước tính phương sai
- Framework nhất quán: Dễ dàng mở rộng cho thiết kế phức tạp hơn (two-way, three-way ANOVA)
- Phương pháp chính thống: Được cộng đồng khoa học chấp nhận rộng rãi
Các phương pháp hiệu chỉnh khác
Nếu vẫn muốn sử dụng multiple t-tests, có thể áp dụng các phương pháp hiệu chỉnh:
- Bonferroni correction: $\alpha_{adjusted} = \frac{\alpha}{k}$, rất bảo thủ
- Holm method: Ít bảo thủ hơn Bonferroni
- False Discovery Rate (FDR): Kiểm soát tỷ lệ phát hiển giả
Mở rộng và ứng dụng nâng cao
Các mở rộng của One-way ANOVA
Khi nắm vững phân tích phương sai một chiều, có thể tìm hiểu các phương pháp mở rộng:
- Two-way ANOVA: Hai biến độc lập phân loại
- Repeated measures ANOVA: Cùng đối tượng đo nhiều lần
- ANCOVA: Kết hợp biến liên tục và phân loại
- MANOVA: Nhiều biến phụ thuộc cùng lúc
Ứng dụng trong nghiên cứu kinh tế
Kinh tế lao động
- Phân tích lương theo ngành: So sánh mức lương giữa các ngành kinh tế
- Hiệu quả đào tạo: Đánh giá tác động của các chương trình đào tạo
- Gender pay gap: Phân tích chênh lệch lương theo giới tính và ngành nghề
Kinh tế vĩ mô
- So sánh khu vực: GDP bình quân đầu người giữa các vùng miền
- Hiệu quả chính sách: Tác động của chính sách tài khóa lên tăng trưởng
- Phân tích ngành: Đóng góp của các ngành vào tổng sản phẩm
Kinh tế doanh nghiệp
- Hiệu quả marketing: So sánh ROI của các chiến lược marketing
- Năng suất lao động: Phân tích theo loại hình doanh nghiệp
- Chất lượng sản phẩm: So sánh giữa các quy trình sản xuất
Báo cáo kết quả nghiên cứu
Cấu trúc báo cáo chuẩn
Khi báo cáo kết quả phân tích phương sai một chiều trong bài báo khoa học, cần tuân thủ cấu trúc chuẩn:
- Mô tả mẫu: Kích thước mẫu tổng thể và từng nhóm
- Kiểm tra giả thiết: Báo cáo kết quả kiểm định Levene và kiểm định tính chuẩn (normality tests)
- Kết quả ANOVA: F-statistic, bậc tự do, giá trị p
- Mức ảnh hưởng (Effect size): Eta-squared hoặc omega-squared
- Post-hoc tests: Kết quả so sánh từng cặp
- Thống kê mô tả: Mean, SD cho từng nhóm
Ví dụ báo cáo
Trình bày kết quả báo cáo
Phân tích phương sai một chiều được thực hiện để so sánh thu nhập trung bình (logarit) giữa ba lĩnh vực kinh tế. Kiểm định Levene cho thấy vi phạm giả thiết đồng nhất phương sai, F(2, 7284) = 45.32, p < 0.001. Do đó, kiểm định Welch được sử dụng thay thế. Kết quả cho thấy có sự khác biệt có ý nghĩa thống kê về thu nhập giữa các lĩnh vực, Welch’s F(2, 3847.23) = 437.89, p < 0.001, eta-squared = 0.109. Kiểm định post-hoc Games-Howell cho thấy thu nhập trong lĩnh vực dịch vụ (M = 3.45, SD = 0.81) cao hơn có ý nghĩa so với công nghiệp (M = 3.18, SD = 0.75, p < 0.001) và nông nghiệp (M = 2.89, SD = 0.68, p < 0.001). Thu nhập công nghiệp cũng cao hơn có ý nghĩa so với nông nghiệp (p < 0.001).
Tài liệu tham khảo
Để nghiên cứu sâu hơn về phân tích phương sai một chiều và ứng dụng trong thực hành kinh tế lượng, các bạn có thể tham khảo các tài liệu sau:
- Gujarati, D. N. & Porter, D. C. (2023): “Basic Econometrics” – McGraw Hill Education (Chương về Analysis of Variance)
- Wooldridge, J. M. (2020): “Introductory Econometrics: A Modern Approach” – Cengage Learning
- Hill, R. C., Griffiths, W. E. & Lim, G. C. (2018): “Principles of Econometrics” – Wiley
- Kennedy, P. (2022): “A Guide to Econometrics” – MIT Press
- Field, A. (2017): “Discovering Statistics Using IBM SPSS Statistics” – SAGE Publications
- Pallant, J. (2020): “SPSS Survival Manual” – McGraw Hill Education
- Montgomery, D. C. (2019): “Design and Analysis of Experiments” – Wiley
- Maxwell, S. E., Delaney, H. D. & Kelley, K. (2017): “Designing Experiments and Analyzing Data” – Routledge