Bảng tra
Trị tới hạn cho kiểm định nghiệm đơn vị ADF
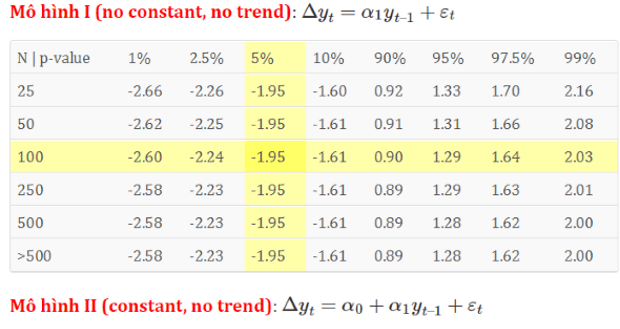
Các kiểm định thống kê cho kiểm định nghiệm đơn vị và đồng kết hợp không tuân theo các phân phối chuẩn. Phần trình bày bên dưới là tổng hợp các giá trị tới hạn cho kiểm định nghiệm đơn vị ADF (Augmented Dickey-Fuller) trong phân tích tính dừng của chuỗi thời gian và dữ liệu bảng.
Mô hình I (no constant, no trend)
Nội dung chính
\(\Delta {y_t} = {\alpha _1}{y_{t – 1}} + {\varepsilon _t}\)
| N | p-value | 1% | 2.5% | 5% | 10% | 90% | 95% | 97.5% | 99% |
| 25 | -2.66 | -2.26 | -1.95 | -1.60 | 0.92 | 1.33 | 1.70 | 2.16 |
| 50 | -2.62 | -2.25 | -1.95 | -1.61 | 0.91 | 1.31 | 1.66 | 2.08 |
| 100 | -2.60 | -2.24 | -1.95 | -1.61 | 0.90 | 1.29 | 1.64 | 2.03 |
| 250 | -2.58 | -2.23 | -1.95 | -1.61 | 0.89 | 1.29 | 1.63 | 2.01 |
| 500 | -2.58 | -2.23 | -1.95 | -1.61 | 0.89 | 1.28 | 1.62 | 2.00 |
| >500 | -2.58 | -2.23 | -1.95 | -1.61 | 0.89 | 1.28 | 1.62 | 2.00 |
Mô hình II (constant, no trend)
\(\Delta {y_t} = {\alpha _0} + {\alpha _1}{y_{t – 1}} + {\varepsilon _t}\)
| N | p-value | 1% | 2.5% | 5% | 10% | 90% | 95% | 97.5% | 99% |
| 25 | -3.75 | -3.33 | -3.00 | -2.62 | -0.37 | 0.00 | 0.34 | 0.72 |
| 50 | -3.58 | -3.22 | -2.93 | -2.60 | -0.40 | -0.03 | 0.29 | 0.66 |
| 100 | -3.51 | -3.17 | -2.89 | -2.58 | -0.42 | -0.05 | 0.26 | 0.63 |
| 250 | -3.46 | -3.14 | -2.88 | -2.57 | -0.42 | -0.06 | 0.24 | 0.62 |
| 500 | -3.44 | -3.13 | -2.87 | -2.57 | -0.43 | -0.07 | 0.24 | 0.61 |
| >500 | -3.43 | -3.12 | -2.86 | -2.57 | -0.44 | -0.07 | 0.23 | 0.60 |
Mô hình III (constant, trend)
\(\Delta {y_t} = {\alpha _0} + {\alpha _1}{y_{t – 1}} + {\alpha _2}t + {\varepsilon _t}\)
| N | p-value | 1% | 2.5% | 5% | 10% | 90% | 95% | 97.5% | 99% |
| 25 | -4.38 | -3.95 | -3.60 | -3.24 | -1.14 | -0.80 | -0.50 | -0.15 |
| 50 | -4.15 | -3.80 | -3.50 | -3.18 | -1.19 | -0.87 | -0.58 | -0.24 |
| 100 | -4.04 | -3.73 | -3.45 | -3.15 | -1.22 | -0.90 | -0.62 | -0.28 |
| 250 | -3.99 | -3.69 | -3.43 | -3.13 | -1.23 | -0.92 | -0.64 | -0.31 |
| 500 | -3.98 | -3.68 | -3.42 | -3.13 | -1.24 | -0.93 | -0.65 | -0.32 |
| >500 | -3.96 | -3.66 | -3.41 | -3.12 | -1.25 | -0.94 | -0.66 | -0.33 |