Hồi quy tuyến tính đa biến
Hướng dẫn thực hành hồi quy tuyến tính đa biến với SPSS

Tóm tắt: Hồi quy tuyến tính đa biến là dạng mở rộng của hồi quy giản đơn, được ứng dụng rộng rãi trong thực hành kinh tế lượng để dự báo và phân tích mối quan hệ giữa nhiều biến. Bài viết hướng dẫn chi tiết cách thực hiện hồi quy đa biến trong SPSS, từ kiểm tra các giả định cần thiết đến diễn giải kết quả, đặc biệt tập trung vào ứng dụng thực tế trong nghiên cứu kinh tế và xã hội.
Giới thiệu về hồi quy tuyến tính đa biến
Nội dung chính
Ví dụ ứng dụng trong kinh tế Việt Nam:
- Dự báo thu nhập của người lao động theo số năm đi học, số năm kinh nghiệm, tuổi, giới tính và khu vực sinh sống
- Phân tích các yếu tố ảnh hưởng đến giá bất động sản như diện tích, vị trí, số phòng ngủ, tuổi nhà
- Nghiên cứu mối quan hệ giữa GDP với đầu tư, xuất khẩu, tiêu dùng và lạm phát
- Đánh giá tác động của các chính sách kinh tế đến tăng trưởng kinh tế
Tài liệu tham khảo bổ sung:
Các biến trong mô hình hồi quy tuyến tính đa biến phải thỏa mãn tính chất BLUE. Để hiểu rõ hơn về ảnh hưởng của các giả định đến kết quả mô hình, tham khảo bài các khuyết tật của mô hình hồi quy.
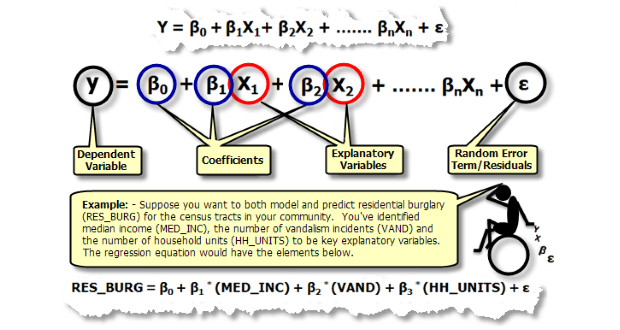
Tính chất BLUE này được thể hiện cụ thể qua các giả định quan trọng của mô hình được trình bày bên dưới.
Các giả định của hồi quy tuyến tính đa biến
Để sử dụng phương pháp hồi quy tuyến tính đa biến trong thực hành kinh tế lượng, dữ liệu phải thỏa mãn bảy giả định quan trọng sau:
1. Tính chất của biến phụ thuộc
Biến phụ thuộc trong mô hình phải là biến liên tục (có thể dạng tỷ lệ hoặc dạng khoảng).
2. Mối quan hệ tuyến tính
Có mối quan hệ tuyến tính giữa biến phụ thuộc với các biến giải thích của mô hình. Có nhiều cách để kiểm tra mối quan hệ tuyến tính này, một trong số đó là sử dụng đồ thị phân tán giữa hai biến.
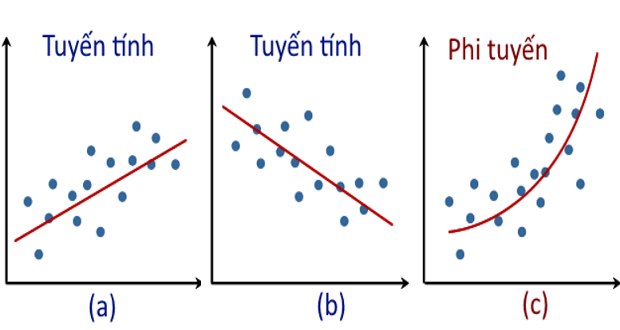
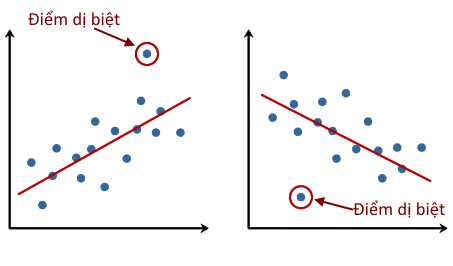
3. Không có điểm dị biệt
Dữ liệu không có chứa các điểm dị biệt (outliers). Xem thêm phương pháp phát hiện điểm dị biệt.
4. Sự độc lập của các quan sát
Có sự độc lập giữa các quan sát trong một biến. Sự độc lập giữa các quan sát có thể được kiểm tra qua kiểm định Durbin-Watson về sự tự tương quan.
5. Đồng nhất phương sai
Phương sai của phần dư bằng nhau hay có sự đồng nhất về phương sai của phần dư (homoscedasticity). Sự đồng nhất về phương sai có thể được đánh giá bằng đồ thị phân tán phần dư.
6. Không có đa cộng tuyến
Không có sự đa cộng tuyến (multicollinearity) giữa các biến giải thích. Điều này có nghĩa các biến giải thích trong mô hình không có sự tương quan cao với nhau.
7. Phân phối chuẩn của phần dư
Sai số của phần dư (residuals errors) ở đường thẳng hồi quy có phân phối chuẩn hoặc xấp xỉ phân phối chuẩn. Xem thêm Phân phối chuẩn.
Dữ liệu mẫu và ví dụ thực tế
Trong hướng dẫn này, chúng ta sử dụng bộ dữ liệu nghiên cứu về các yếu tố ảnh hưởng đến khả năng đọc hiểu của trẻ em. Tải dữ liệu hồi quy đa biến
Mô tả dữ liệu:
- read: Khả năng đọc hiểu của trẻ (điểm số) – biến phụ thuộc
- age: Tuổi của trẻ (năm) – biến độc lập
- mem: Khả năng ghi nhớ (điểm số) – biến độc lập
- iq: Chỉ số IQ (điểm số) – biến độc lập
Câu hỏi nghiên cứu: Tuổi, chỉ số IQ và khả năng ghi nhớ của trẻ có ảnh hưởng đến khả năng đọc hiểu không và mức độ ảnh hưởng như thế nào?
Đây là một ví dụ điển hình trong thực hành kinh tế lượng ứng dụng, tương tự như nghiên cứu các yếu tố ảnh hưởng đến học tập, năng suất lao động, hoặc hiệu quả kinh doanh.
Hướng dẫn thực hành chi tiết
Trong SPSS, điều hướng đến menu phân tích hồi quy:
Analyze → Regression → Linear…
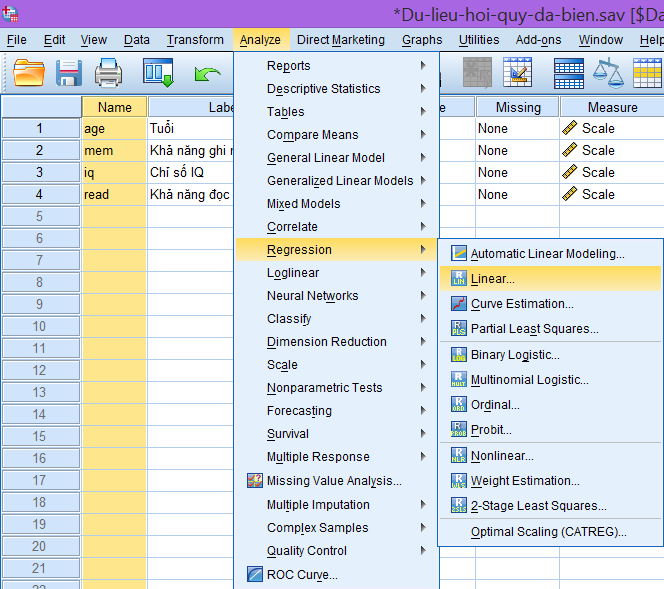
Bước 2: Thiết lập biến phụ thuộc và biến độc lập
Cửa sổ Linear Regression mở ra, thực hiện các thiết lập sau:
- Đưa biến read vào ô Dependent
- Đưa biến age, mem và iq vào ô Independent(s)
- Đảm bảo phương thức Enter được chọn ở phần Method
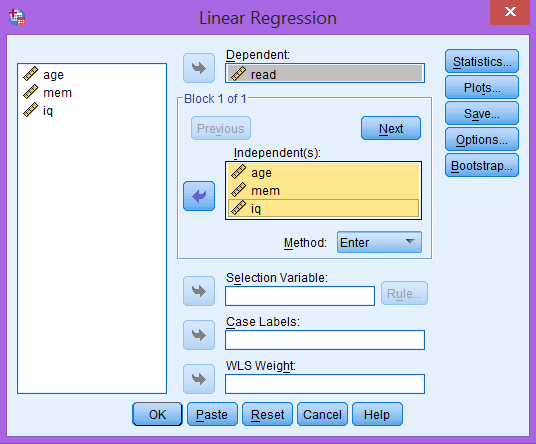
Bước 3: Cấu hình tùy chọn thống kê
Click nút Statistics… để thiết lập các tùy chọn:
Trong khung Regression Coefficients:
- Chọn Estimates để hiển thị các tham số ước lượng
- Chọn Confidence intervals để hiển thị khoảng tin cậy cho tham số
Các tùy chọn bổ sung:
- Chọn Model fit để kiểm tra độ phù hợp của mô hình
- Chọn Collinearity diagnostics để kiểm tra hiện tượng đa cộng tuyến
- Trong khung Residuals, chọn Durbin-Watson để kiểm tra sự tự tương quan
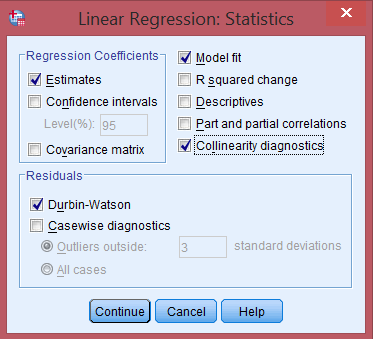
Bước 4: Thiết lập đồ thị chẩn đoán
Click nút Plots… để vẽ đồ thị chẩn đoán:
Thiết lập đồ thị:
- Chọn *ZRESID (Standardized Residuals) cho trục Y
- Chọn *ZPRED (Standardized Predicted Values) cho trục X
- Chọn Histogram và Normal probability plot để kiểm tra phân phối chuẩn
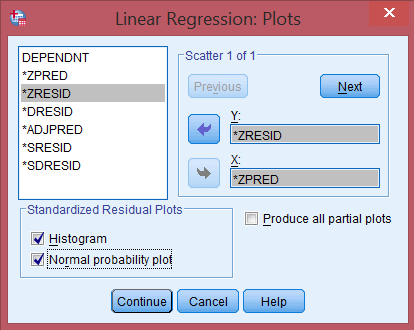
Bước 5: Kiểm tra tùy chọn bổ sung
Click nút Options… để đảm bảo:
- Mục Include constant in equation được chọn (để sử dụng kiểm định Durbin-Watson)
- Các tùy chọn khác để mặc định
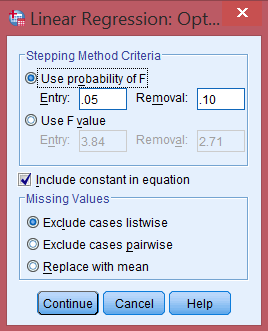
Bước 6: Thực thi phân tích
Sau mỗi bước thiết lập, click Continue để quay về cửa sổ chính, sau đó click OK để thực hiện phân tích.
Đọc và diễn giải kết quả
Bảng ANOVA – Kiểm tra độ phù hợp tổng thể
Bảng ANOVA tóm tắt các kết quả về độ phù hợp của mô hình nghiên cứu:

Các thông số quan trọng:
- Hệ số ý nghĩa (Sig): Cho biết mô hình có giải thích được sự thay đổi của biến phụ thuộc hay không. Nếu Sig > 0.05, mô hình không phù hợp với dữ liệu
- Giá trị F: So sánh mô hình hồi quy với mô hình chỉ có hằng số. Kiểm định giả thuyết \(H_0: \beta_1 = \beta_2 = \beta_3 = 0\)
- Sum of Squares: Bao gồm ESS (Regression: 7.498), RSS (Residual: 1.482), và TSS (Total: 8.980)
Công thức quan trọng: \(TSS = ESS + RSS\), trong đó:
- ESS: Tổng bình phương thay đổi được giải thích bởi mô hình
- RSS: Tổng bình phương của phần dư
- TSS: Tổng thay đổi trong biến phụ thuộc
Khả năng giải thích \(R^2 = \frac{ESS}{TSS}\) là tỷ lệ thay đổi được giải thích bởi mô hình.
Bảng Model Summary – Đánh giá độ phù hợp
Bảng Model Summary trình bày kết quả tóm tắt về độ phù hợp của mô hình:

Diễn giải các chỉ số:
- R-square (0.835): 83.5% sự thay đổi trong biến phụ thuộc được giải thích bởi mô hình
- Adjusted R-square (0.804): 80.4% phương sai của biến phụ thuộc được giải thích sau khi điều chỉnh cho số biến
- Std. Error of Estimate (4.468): Sai số chuẩn của ước lượng, đo mức độ phân tán quanh giá trị dự báo
- Durbin-Watson (2.029): Giá trị trong khoảng 1.5-2.5 cho thấy không có sự tự tương quan bậc 1
Bảng Coefficients – Hệ số hồi quy
Bảng Coefficients trình bày các hệ số của phương trình hồi quy:
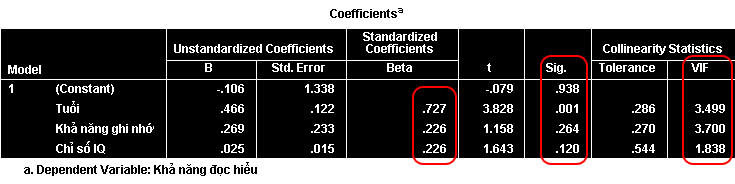
Diễn giải kết quả:
- Chỉ có hệ số của biến age có ý nghĩa thống kê (p < 0.05)
- Tuổi có ảnh hưởng đến khả năng đọc hiểu của trẻ
- Chưa có bằng chứng về tác động của IQ và khả năng ghi nhớ
Kiểm tra đa cộng tuyến:
- Cột Collinearity Statistics kiểm tra mức độ đa cộng tuyến
- Hệ số VIF từ 1.8 đến 3.5 (< 10) cho thấy không có đa cộng tuyến nghiêm trọng
Đồ thị chẩn đoán
Histogram và Normal P-P Plot:
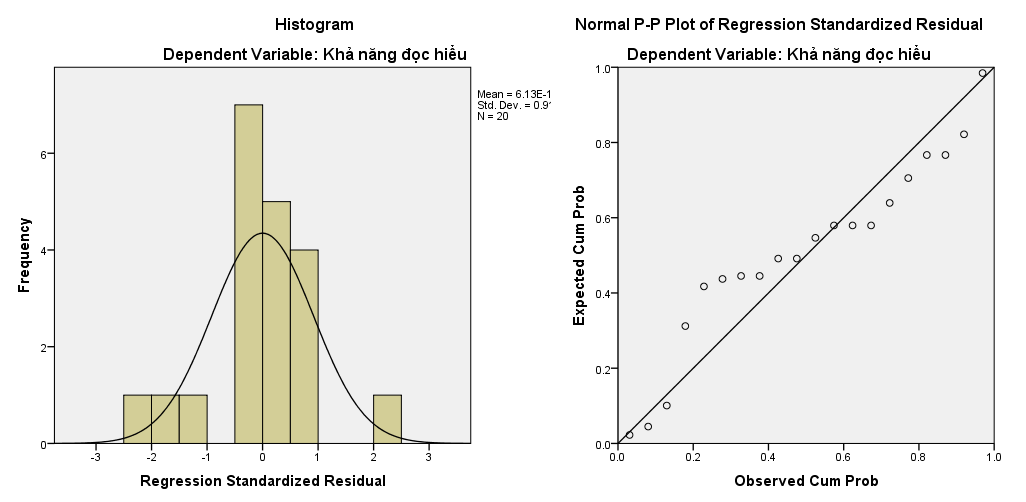
Đồ thị histogram cho thấy phân phối của phần dư có hình dạng phân phối chuẩn. Đồ thị Normal P-P cho thấy các quan sát phân phối xấp xỉ đường thẳng ứng với phân phối chuẩn.
Scatter Plot phần dư:
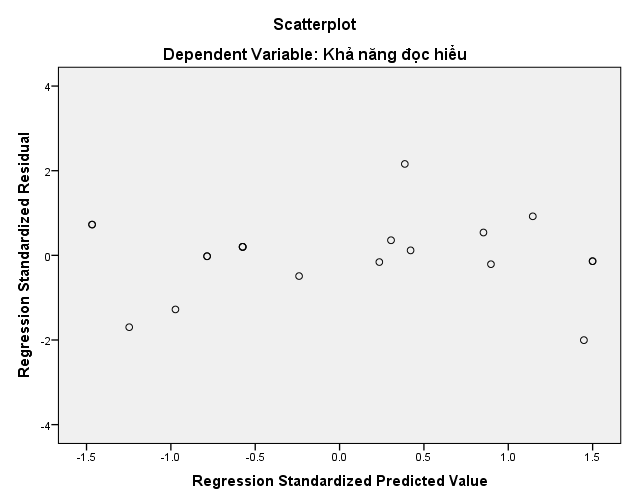
Lưu ý quan trọng
Tác động của vi phạm giả thuyết
Sự vi phạm giả thuyết phương sai đồng nhất trong thực hành kinh tế lượng:
- Không ảnh hưởng: Độ phù hợp \(R^2\) và hệ số ước lượng \(\beta\) vẫn không thiên lệch
- Ảnh hưởng: Sai số chuẩn của ước lượng không chính xác
- Hậu quả: Giá trị thống kê F, t và mức ý nghĩa có thể sai lệch
- Giải pháp: Sử dụng sai số chuẩn robust hoặc biến đổi dữ liệu
Các biện pháp khắc phục
- Phương sai không đồng nhất: Sử dụng ước lượng bình phương tối thiểu trọng số, WLS (Weighted Least Squares) hoặc hồi quy với sai số vững mạnh (robust standard errors).
- Đa cộng tuyến: Loại bỏ biến có VIF cao, sử dụng hồi quy Ridge (Ridge regression) hoặc phân tích thành phần chính, PCA (Principal Component Analysis).
- Tự tương quan: Sử dụng ước lượng bình phương tối thiểu tuyến tính tổng quát, GLS (Generalized Least Squares) hoặc thêm các biến trễ (lag variables)
- Phi tuyến tính: Biến đổi biến hoặc sử dụng hồi quy đa thức (polynomial regression).
Ứng dụng trong nghiên cứu kinh tế
Hồi quy tuyến tính đa biến có nhiều ứng dụng quan trọng trong thực hành kinh tế lượng:
- Kinh tế vĩ mô: Phân tích các yếu tố ảnh hưởng đến GDP, lạm phát, thất nghiệp
- Tài chính: Mô hình định giá tài sản, dự báo giá chứng khoán, phân tích rủi ro
- Marketing: Nghiên cứu tác động của quảng cáo, giá cả, chất lượng đến doanh số
- Nhân sự: Phân tích các yếu tố ảnh hưởng đến lương, năng suất, sự hài lòng
Tổng kết
Hồi quy tuyến tính đa biến là công cụ mạnh mẽ và linh hoạt trong thực hành kinh tế lượng. Thông qua hướng dẫn này, chúng ta đã nắm vững:
- Các giả định cần thiết và cách kiểm tra chúng
- Quy trình thực hiện hồi quy đa biến trong SPSS từ A đến Z
- Cách đọc và diễn giải các bảng kết quả quan trọng
- Phương pháp chẩn đoán và xử lý vi phạm giả thuyết
- Ứng dụng thực tế trong nghiên cứu kinh tế và xã hội
Key Points:
- Kiểm tra giả thuyết là bước quan trọng nhất trước khi diễn giải kết quả
- Bảng ANOVA xác định tính phù hợp tổng thể của mô hình
- R-square cho biết tỷ lệ biến thiên được giải thích bởi mô hình
- VIF < 10 cho thấy không có đa cộng tuyến nghiêm trọng
- Durbin-Watson (1.5-2.5) cho thấy không có tự tương quan
Việc thành thạo hồi quy tuyến tính đa biến sẽ trang bị cho các nhà nghiên cứu công cụ phân tích mạnh mẽ để đưa ra những kết luận chính xác và có ý nghĩa trong thực hành kinh tế lượng.
1. Một quy tắc kinh nghiệm được sử dụng để kết luận không có sự tự tương quan bậc 1 là nếu giá trị thống kê d nằm giữa 1.5 và 2.5. Giá trị d nhỏ hơn 1.5 cho biết có sự tự tương quan dương bậc 1. Giá trị d lớn hơn 2.5 cho biết có sự tự tương quan âm bậc 1.
2. Hoàng Ngọc Nhậm và cộng sự, 2008. Giáo trình kinh tế lượng. Hà Nội: Nhà xuất bản lao động – xã hội, trang 140.
Phụ lục: Code syntax cho các phần mềm thống kê
SPSS Syntax
SPSS Syntax (.sps)
* Hồi quy tuyến tính đa biến với SPSS
* Tác giả: Hướng dẫn thực hành kinh tế lượng
* Thống kê mô tả cơ bản
DESCRIPTIVES VARIABLES=read age mem iq
/STATISTICS=MEAN STDDEV MIN MAX.
* Ma trận tương quan
CORRELATIONS
/VARIABLES=read age mem iq
/PRINT=TWOTAIL NOSIG
/MISSING=PAIRWISE.
* Hồi quy tuyến tính đa biến
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA COLLIN
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT read
/METHOD=ENTER age mem iq
/SCATTERPLOT=(*ZRESID ,*ZPRED)
/RESIDUALS DURBIN HISTOGRAM(ZRESID) NORMPROB(ZRESID).
* Kiểm tra điểm dị biệt
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT read
/METHOD=ENTER age mem iq
/SAVE COOK LEVER DFBETA DFFIT
/RESIDUALS OUTLIERS(COOK) OUTLIERS(LEVER).
* Kiểm tra tính tuyến tính
GRAPH
/SCATTERPLOT(BIVAR)=age WITH read
/MISSING=LISTWISE.
GRAPH
/SCATTERPLOT(BIVAR)=mem WITH read
/MISSING=LISTWISE.
GRAPH
/SCATTERPLOT(BIVAR)=iq WITH read
/MISSING=LISTWISE.
* Biến đổi dữ liệu nếu cần
COMPUTE ln_read = LN(read).
COMPUTE sqrt_read = SQRT(read).
EXECUTE.
Stata Commands
Stata Commands (.do)
* Hồi quy tuyến tính đa biến trong Stata
* Sử dụng dữ liệu về khả năng đọc hiểu
* Tải và mô tả dữ liệu
use "ols_data.dta", clear
describe read age mem iq
summarize read age mem iq, detail
* Ma trận tương quan
corr read age mem iq
pwcorr read age mem iq, sig
* Hồi quy tuyến tính đa biến
regress read age mem iq
* Kiểm tra các giả thuyết
* 1. Kiểm tra đa cộng tuyến (VIF)
estat vif
* 2. Kiểm tra phương sai đồng nhất (Breusch-Pagan test)
estat hettest
* 3. Kiểm tra tự tương quan (Durbin-Watson)
estat dwatson
* 4. Kiểm tra phân phối chuẩn của phần dư
predict residuals, residuals
histogram residuals, normal
qnorm residuals
* 5. Kiểm tra tính tuyến tính
scatter read age || lfit read age
scatter read mem || lfit read mem
scatter read iq || lfit read iq
* 6. Kiểm tra điểm dị biệt
predict leverage, leverage
predict cooksd, cooksd
predict dfbeta_age, dfbeta(age)
predict dfbeta_mem, dfbeta(mem)
predict dfbeta_iq, dfbeta(iq)
* Liệt kê các quan sát có Cook's distance > 4/n
scalar threshold = 4/_N
list if cooksd > threshold
* Robust standard errors nếu có phương sai không đồng nhất
regress read age mem iq, robust
* Weighted least squares nếu cần
regress read age mem iq [aweight=1/variance_weight]
* Stepwise regression
stepwise, pr(0.05) pe(0.10): regress read age mem iq
* Thống kê mô tả theo nhóm nếu có biến categorical
* egen age_group = cut(age), group(3)
* by age_group: summarize read
R Script
R Script (.R)
# Hồi quy tuyến tính đa biến với R
# Sử dụng các gói car, lmtest và ggplot2
# Tải các thư viện cần thiết
library(car)
library(lmtest)
library(ggplot2)
library(dplyr)
library(corrplot)
library(stargazer)
# Đọc dữ liệu
data <- read.csv("ols_data.csv")
str(data)
summary(data)
# Thống kê mô tả
summary(data[c("read", "age", "mem", "iq")])
# Ma trận tương quan
cor_matrix <- cor(data[c("read", "age", "mem", "iq")])
print(cor_matrix)
corrplot(cor_matrix, method = "circle")
# Hồi quy tuyến tính đa biến
model <- lm(read ~ age + mem + iq, data = data)
summary(model)
# Kiểm tra các giả thuyết
# 1. Kiểm tra đa cộng tuyến
vif_values <- vif(model)
print(vif_values)
# 2. Kiểm tra phương sai đồng nhất
# Breusch-Pagan test
bptest(model)
# 3. Kiểm tra tự tương quan
# Durbin-Watson test
dwtest(model)
# 4. Kiểm tra phân phối chuẩn của phần dư
# Shapiro-Wilk test
shapiro.test(residuals(model))
# 5. Đồ thị chẩn đoán
par(mfrow = c(2, 2))
plot(model)
# 6. Kiểm tra tính tuyến tính
# Scatter plots
ggplot(data, aes(x = age, y = read)) +
geom_point() +
geom_smooth(method = "lm") +
labs(title = "Mối quan hệ giữa Age và Read")
ggplot(data, aes(x = mem, y = read)) +
geom_point() +
geom_smooth(method = "lm") +
labs(title = "Mối quan hệ giữa Memory và Read")
ggplot(data, aes(x = iq, y = read)) +
geom_point() +
geom_smooth(method = "lm") +
labs(title = "Mối quan hệ giữa IQ và Read")
# 7. Kiểm tra điểm dị biệt
# Cook's distance
cooksd <- cooks.distance(model)
plot(cooksd, pch = "*", cex = 2, main = "Cook's Distance")
abline(h = 4/length(cooksd), col = "red")
# Leverage
leverage <- hatvalues(model)
plot(leverage, pch = "*", cex = 2, main = "Leverage")
# Standardized residuals
std_residuals <- rstandard(model)
plot(std_residuals, pch = "*", cex = 2, main = "Standardized Residuals")
# 8. Robust standard errors (nếu cần)
library(sandwich)
coeftest(model, vcov = vcovHC(model, type = "HC0"))
# 9. Weighted Least Squares (nếu cần)
# weights <- 1/fitted(lm(abs(residuals(model)) ~ fitted(model)))^2
# model_wls <- lm(read ~ age + mem + iq, data = data, weights = weights)
# 10. Stepwise regression
model_stepwise <- step(model, direction = "both")
summary(model_stepwise)
# 11. Tạo bảng kết quả đẹp
stargazer(model, type = "text",
title = "Kết quả hồi quy tuyến tính đa biến",
dep.var.labels = "Khả năng đọc hiểu",
covariate.labels = c("Tuổi", "Khả năng ghi nhớ", "Chỉ số IQ"))
# 12. Dự báo
new_data <- data.frame(age = 10, mem = 50, iq = 100)
prediction <- predict(model, new_data, interval = "confidence")
print(prediction)
Python Script
Python Script (.py)
# Hồi quy tuyến tính đa biến với Python
# Sử dụng scikit-learn, statsmodels và seaborn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score, mean_squared_error
from sklearn.preprocessing import StandardScaler
from statsmodels.stats.outliers_influence import variance_inflation_factor
import statsmodels.api as sm
from statsmodels.stats.diagnostic import het_breuschpagan, linear_rainbow
from statsmodels.stats.stattools import durbin_watson
# Đọc dữ liệu
data = pd.read_csv('ols_data.csv')
print(data.info())
print(data.describe())
# Kiểm tra missing values
print(data.isnull().sum())
# Thống kê mô tả
variables = ['read', 'age', 'mem', 'iq']
desc_stats = data[variables].describe()
print(desc_stats)
# Ma trận tương quan
correlation_matrix = data[variables].corr()
print(correlation_matrix)
# Vẽ heatmap tương quan
plt.figure(figsize=(8, 6))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', center=0)
plt.title('Ma trận tương quan')
plt.show()
# Scatter plots để kiểm tra tính tuyến tính
fig, axes = plt.subplots(1, 3, figsize=(15, 5))
sns.scatterplot(data=data, x='age', y='read', ax=axes[0])
sns.regplot(data=data, x='age', y='read', ax=axes[0], scatter=False)
axes[0].set_title('Age vs Read')
sns.scatterplot(data=data, x='mem', y='read', ax=axes[1])
sns.regplot(data=data, x='mem', y='read', ax=axes[1], scatter=False)
axes[1].set_title('Memory vs Read')
sns.scatterplot(data=data, x='iq', y='read', ax=axes[2])
sns.regplot(data=data, x='iq', y='read', ax=axes[2], scatter=False)
axes[2].set_title('IQ vs Read')
plt.tight_layout()
plt.show()
# Chuẩn bị dữ liệu
X = data[['age', 'mem', 'iq']]
y = data['read']
# Hồi quy với scikit-learn
model_sklearn = LinearRegression()
model_sklearn.fit(X, y)
# Kết quả cơ bản
print("Sklearn Results:")
print(f"R² Score: {model_sklearn.score(X, y):.4f}")
print(f"Intercept: {model_sklearn.intercept_:.4f}")
print("Coefficients:")
for i, coef in enumerate(model_sklearn.coef_):
print(f" {X.columns[i]}: {coef:.4f}")
# Hồi quy với statsmodels (chi tiết hơn)
X_with_const = sm.add_constant(X)
model_sm = sm.OLS(y, X_with_const).fit()
print("\nStatsmodels Results:")
print(model_sm.summary())
# Kiểm tra các giả thuyết
print("\n=== KIỂM TRA GIẢ THUYẾT ===")
# 1. Kiểm tra đa cộng tuyến (VIF)
print("\n1. Variance Inflation Factor (VIF):")
vif_data = pd.DataFrame()
vif_data["Variable"] = X.columns
vif_data["VIF"] = [variance_inflation_factor(X.values, i) for i in range(X.shape[1])]
print(vif_data)
# 2. Kiểm tra phương sai đồng nhất (Breusch-Pagan test)
print("\n2. Breusch-Pagan Test (Homoscedasticity):")
bp_test = het_breuschpagan(model_sm.resid, X_with_const)
bp_labels = ['LM Statistic', 'LM-Test p-value', 'F-Statistic', 'F-Test p-value']
print(dict(zip(bp_labels, bp_test)))
# 3. Kiểm tra tự tương quan (Durbin-Watson)
print("\n3. Durbin-Watson Test:")
dw_statistic = durbin_watson(model_sm.resid)
print(f"Durbin-Watson statistic: {dw_statistic:.4f}")
# 4. Kiểm tra phân phối chuẩn của phần dư
print("\n4. Shapiro-Wilk Test (Normality):")
shapiro_stat, shapiro_p = stats.shapiro(model_sm.resid)
print(f"Shapiro-Wilk statistic: {shapiro_stat:.4f}, p-value: {shapiro_p:.4f}")
# 5. Đồ thị chẩn đoán
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
# Residuals vs Fitted
fitted_values = model_sm.fittedvalues
residuals = model_sm.resid
axes[0, 0].scatter(fitted_values, residuals)
axes[0, 0].axhline(y=0, color='red', linestyle='--')
axes[0, 0].set_xlabel('Fitted values')
axes[0, 0].set_ylabel('Residuals')
axes[0, 0].set_title('Residuals vs Fitted')
# Q-Q plot
stats.probplot(residuals, dist="norm", plot=axes[0, 1])
axes[0, 1].set_title('Q-Q Plot')
# Histogram của residuals
axes[1, 0].hist(residuals, bins=20, edgecolor='black')
axes[1, 0].set_xlabel('Residuals')
axes[1, 0].set_ylabel('Frequency')
axes[1, 0].set_title('Histogram of Residuals')
# Scale-Location plot
axes[1, 1].scatter(fitted_values, np.sqrt(np.abs(residuals)))
axes[1, 1].set_xlabel('Fitted values')
axes[1, 1].set_ylabel('√|Residuals|')
axes[1, 1].set_title('Scale-Location Plot')
plt.tight_layout()
plt.show()
# 6. Kiểm tra điểm dị biệt
print("\n6. Outlier Detection:")
# Cook's distance
influence = model_sm.get_influence()
cook_distance = influence.cooks_distance[0]
leverage = influence.hat_matrix_diag
dfbetas = influence.dfbetas
print(f"Max Cook's Distance: {cook_distance.max():.4f}")
print(f"Threshold (4/n): {4/len(data):.4f}")
# Vẽ đồ thị Cook's distance
plt.figure(figsize=(10, 6))
plt.subplot(1, 2, 1)
plt.scatter(range(len(cook_distance)), cook_distance)
plt.axhline(y=4/len(data), color='red', linestyle='--', label='Threshold')
plt.xlabel('Observation')
plt.ylabel("Cook's Distance")
plt.title("Cook's Distance")
plt.legend()
# Vẽ đồ thị Leverage
plt.subplot(1, 2, 2)
plt.scatter(range(len(leverage)), leverage)
plt.axhline(y=2*X.shape[1]/len(data), color='red', linestyle='--', label='Threshold')
plt.xlabel('Observation')
plt.ylabel('Leverage')
plt.title('Leverage')
plt.legend()
plt.tight_layout()
plt.show()
# 7. Dự báo
print("\n7. Prediction Example:")
new_data = pd.DataFrame({
'age': [10],
'mem': [50],
'iq': [100]
})
prediction_sklearn = model_sklearn.predict(new_data)
print(f"Sklearn prediction: {prediction_sklearn[0]:.2f}")
new_data_with_const = sm.add_constant(new_data)
prediction_sm = model_sm.predict(new_data_with_const)
confidence_interval = model_sm.get_prediction(new_data_with_const).conf_int()
print(f"Statsmodels prediction: {prediction_sm[0]:.2f}")
print(f"95% Confidence Interval: [{confidence_interval[0,0]:.2f}, {confidence_interval[0,1]:.2f}]")
# 8. Model comparison và feature selection
from sklearn.feature_selection import f_regression
print("\n8. Feature Importance:")
f_stats, f_pvalues = f_regression(X, y)
feature_importance = pd.DataFrame({
'Feature': X.columns,
'F-statistic': f_stats,
'p-value': f_pvalues
}).sort_values('F-statistic', ascending=False)
print(feature_importance)
# 9. Robust regression (nếu cần)
print("\n9. Robust Regression Results:")
robust_model = sm.RLM(y, X_with_const).fit()
print(robust_model.summary())
Tài liệu tham khảo
- Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics (5th ed.). SAGE Publications.
- Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2019). Multivariate Data Analysis (8th ed.). Cengage Learning.
- Hoàng Ngọc Nhậm và cộng sự. (2008). Giáo trình kinh tế lượng. Hà Nội: Nhà xuất bản Lao động – Xã hội.
- IBM Corporation. (2023). IBM SPSS Statistics Documentation – Regression. Retrieved from IBM Knowledge Center.
- Montgomery, D. C., Peck, E. A., & Vining, G. G. (2021). Introduction to Linear Regression Analysis (6th ed.). John Wiley & Sons.
- Chatterjee, S., & Hadi, A. S. (2015). Regression Analysis by Example (5th ed.). John Wiley & Sons.
- Wooldridge, J. M. (2020). Introductory Econometrics: A Modern Approach (7th ed.). Cengage Learning.