Điểm dị biệt – Outliers
Phát hiện và xử lý điểm dị biệt trong thực hành kinh tế lượng với SPSS

Tóm tắt: Điểm dị biệt (outliers) là vấn đề quan trọng trong thực hành kinh tế lượng, có thể làm méo mó kết quả phân tích và vi phạm các giả định thống kê. Bài viết hướng dẫn chi tiết cách phát hiện điểm dị biệt univariate và multivariate trên SPSS, phân tích boxplot, áp dụng các công thức toán học để xác định ngưỡng, và trình bày các phương pháp xử lý phù hợp với nghiên cứu kinh tế Việt Nam.
Giới thiệu về điểm dị biệt trong thực hành kinh tế lượng
Nội dung chính
- Giới thiệu về điểm dị biệt trong thực hành kinh tế lượng
- Phân loại điểm dị biệt
- Dữ liệu mẫu và thiết lập
- Hướng dẫn thực hành chi tiết trên SPSS
- Phương pháp xử lý điểm dị biệt
- Lưu ý quan trọng khi xử lý điểm dị biệt
- Ứng dụng trong nghiên cứu kinh tế Việt Nam
- Tổng kết
- Phụ lục – Code cho các phần mềm khác
- Tài liệu tham khảo
Trong thực hành kinh tế lượng, các điểm dị biệt (outliers) là những điểm có giá trị khác xa so với phần còn lại của dữ liệu. Việc xác định giá trị của điểm dị biệt có tính chủ quan, tuy nhiên có một số tiêu chuẩn khách quan để xác định một điểm có phải là điểm dị biệt hay không.
Trong nghiên cứu kinh tế Việt Nam, điểm dị biệt thường xuất hiện trong các bối cảnh như:
- Thu nhập của một số hộ gia đình cao bất thường so với mức trung bình
- Doanh thu của doanh nghiệp trong một thời điểm đặc biệt (khuyến mãi lớn, sự kiện)
- Điểm thi của học sinh xuất sắc hoặc yếu kém đặc biệt
- Giá cổ phiếu biến động mạnh trong những ngày có tin tức quan trọng
Có nên kiểm tra và loại bỏ điểm dị biệt không?
Đây là câu hỏi quan trọng trong thực hành kinh tế lượng. Có nhiều quan điểm khác nhau về việc xử lý điểm dị biệt:
Lý do ủng hộ việc xử lý điểm dị biệt
Ảnh hưởng đến tính chuẩn hóa: Các điểm dị biệt có thể làm méo mó tính chuẩn hóa của dữ liệu. Vì sự chuẩn hóa dữ liệu (phân phối chuẩn) là một trong những giả định quan trọng cho đa số các kiểm định thống kê, do vậy chúng ta cần kiểm tra và xử lý ảnh hưởng của các điểm dị biệt.
Lý do không nên loại bỏ điểm dị biệt
- Mâu thuẫn với mục đích nghiên cứu: Thực hiện nghiên cứu nhằm khám phá thế giới thực tế. Nếu người được phỏng vấn trả lời như vậy thì dữ liệu đó phản ánh thực tế
- Tính phổ biến: Điểm dị biệt xuất hiện rất nhiều trong nghiên cứu. Với số lượng lớn biến, bạn luôn phát hiện được điểm dị biệt
- Thang đo tổng hợp: Một biến có thể được đo lường bằng tổ hợp các câu hỏi, giảm khả năng xuất hiện điểm dị biệt
- Hiệu ứng domino: Sau khi loại bỏ điểm dị biệt cũ, có thể xuất hiện điểm dị biệt mới
Phân loại điểm dị biệt
Trong thực hành kinh tế lượng, có hai loại điểm dị biệt chính cần quan tâm:
Điểm dị biệt univariate
Univariate outliers là những giá trị tột cùng trong một biến đơn lẻ. Đây là loại điểm dị biệt cơ bản nhất và dễ phát hiện nhất.Ví dụ trong kinh tế Việt Nam:
- Thu nhập hàng tháng của một hộ gia đình là 100 triệu đồng trong khi thu nhập trung bình là 10 triệu đồng
- Điểm thi đại học của một thí sinh là 29/30 trong khi điểm trung bình là 20/30
- Doanh thu tháng 12 của cửa hàng là 5 tỷ đồng trong khi các tháng khác chỉ 500 triệu đồng
Điểm dị biệt multivariate
Multivariate outliers là những giá trị tột cùng kết hợp của hai hay nhiều biến. Loại này phức tạp hơn và cần công cụ đặc biệt để phát hiện.Ví dụ thực tế:
Trường hợp chiều cao – cân nặng: Một người cao 1m50 nặng 90kg hoặc cao 1m80 nặng 45kg có thể không phải điểm dị biệt khi xét riêng lẻ, nhưng là điểm dị biệt khi xét tổ hợp hai biến này.
Dữ liệu mẫu và thiết lập
Để minh họa các kỹ thuật phát hiện điểm dị biệt trong thực hành kinh tế lượng, chúng ta sử dụng bộ dữ liệu Phân tích dữ liệu chứa thông tin về các biến kinh tế – xã hội.
Tải về dữ liệu mẫuHướng dẫn thực hành chi tiết trên SPSS
Phần 1: Phát hiện điểm dị biệt univariate không phân nhóm
Đây là bước đầu tiên và quan trọng nhất trong việc phát hiện điểm dị biệt. Chúng ta sẽ kiểm tra từng biến một cách độc lập.
Bước 1: Truy cập công cụ Explore
Để thực hiện phân tích điểm dị biệt trong SPSS, các bạn thực hiện theo trình tự:
- Chọn Analyze → Descriptive Statistics → Explore
- Chuyển tất cả các biến liên tục vào cửa sổ Dependent List
- Lưu ý rằng điểm dị biệt chỉ áp dụng cho biến định lượng, không bao gồm biến chuỗi
Bước 2: Cấu hình thống kê
Để có được kết quả phân tích điểm dị biệt đầy đủ:
- Bấm Statistics và chọn Outliers
- Bấm Plots và bỏ chọn mục Stem-and-leaf
- Bấm OK để thực hiện phân tích
Bước 3: Giải thích kết quả
Kết quả phân tích điểm dị biệt univariate cho biến system1 được hiển thị như sau:

Bảng Descriptives
Bảng Descriptives cung cấp thông tin quan trọng:
- Skewness (độ trôi): Đo lường mức độ lệch của phân phối so với phân phối chuẩn
- Kurtosis (độ nhọn): Đo lường độ nhọn của phân phối
- 5% Trimmed Mean: Giá trị trung bình sau khi loại bỏ 5% giá trị cao nhất và thấp nhất
Mẹo phân tích: Bằng cách so sánh 5% Trimmed Mean với Mean, các bạn có thể xác định xem có các giá trị tột cùng ảnh hưởng đến biến hay không. Nếu hai giá trị này chênh lệch nhiều, có thể có điểm dị biệt.
Bảng Extreme Values và Boxplot
Bảng Extreme Values và đồ thị Boxplot có mối liên quan chặt chẽ:

Phần 2: Hiểu về đồ thị boxplot
Đồ thị boxplot là công cụ quan trọng nhất để trực quan hóa điểm dị biệt trong thực hành kinh tế lượng.
Các thành phần của boxplot
- Median (trung vị): Đường thẳng màu đen ở giữa hộp
- Phân vị 1 và 3: Các cạnh dưới và trên của hộp (25% và 75%)
- Khoảng phân vị, IQR (Interquartile Range): Chiều cao của hộp
- Whiskers: Các đường kéo dài từ hộp đến giá trị min/max hợp lệ
- Outliers: Các điểm nằm ngoài whiskers
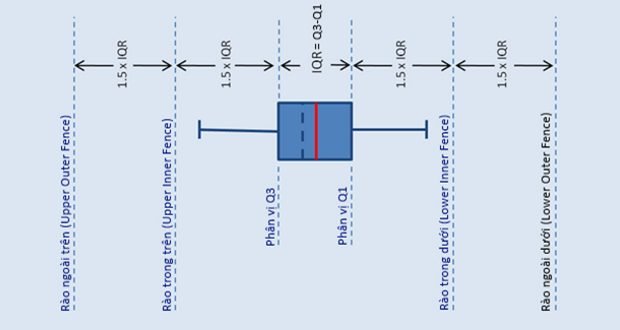
Phân loại điểm dị biệt trong boxplot
SPSS phân biệt hai loại điểm dị biệt:
Điểm dị biệt cứng (mild outliers): Được thể hiện bằng dấu chấm tròn (o), có giá trị chênh lệch 1.5 lần IQR so với Q1 hoặc Q3.
Điểm dị biệt cực mạnh (extreme outliers): Được thể hiện bằng dấu sao (*), có giá trị chênh lệch 3 lần IQR so với Q1 hoặc Q3.
Phần 3: Công thức toán học xác định điểm dị biệt
Các công thức chính để xác định điểm dị biệt trong thực hành kinh tế lượng:
Điểm dị biệt cực mạnh
- Upper Outer Fence (UOF) = Q3 + 3 × IQ
- Lower Outer Fence (LOF) = Q1 – 3 × IQ
Điểm dị biệt cứng
- Upper Inner Fence (UIF) = Q3 + 1.5 × IQ
- Lower Inner Fence (LIF) = Q1 – 1.5 × IQ
Trong đó:
- Q1 và Q3 lần lượt là các phân vị 25% và 75%
- IQ = Q3 – Q1 được gọi là khoảng bên trong phân vị
- Các quan sát có giá trị nằm ngoài UOF và LOF được xem là điểm dị biệt cực mạnh
- Các quan sát có giá trị nằm ngoài UIF và LIF được gọi là điểm dị biệt cứng
Phần 4: Phát hiện điểm dị biệt theo nhóm
Trong nhiều nghiên cứu kinh tế, chúng ta cần phân tích điểm dị biệt trong các nhóm khác nhau. Ví dụ: kiểm tra điểm dị biệt thu nhập theo giới tính.
Các bước thực hiện
- Chọn Analyze → Descriptive Statistics → Explore
- Chuyển các biến liên tục vào cửa sổ Variable(s)
- Chuyển biến phân loại (sex) vào ô Factor List
- Bấm Statistics và chọn Outliers
- Bấm OK để thực hiện
Kết quả phân tích theo nhóm

Kết quả sẽ hiển thị thống kê mô tả riêng biệt cho từng nhóm, giúp so sánh sự khác biệt giữa các nhóm.


Lợi ích của phân tích theo nhóm: Cho phép phát hiện điểm dị biệt có thể bình thường trong tổng thể nhưng bất thường trong nhóm cụ thể, hoặc ngược lại.
Phần 5: Điểm dị biệt multivariate
Điểm dị biệt multivariate phức tạp hơn và thường được đề cập chi tiết trong phân tích tương quan và hồi quy. Đây là chủ đề nâng cao sẽ được trình bày kỹ hơn trong các bài học về phân tích hồi quy.Ghi chú: Phân tích điểm dị biệt đa biến (multivariate) đòi hỏi kỹ thuật thống kê nâng cao như Mahalanobis distance, Cook’s distance, và sẽ được trình bày chi tiết trong phần phân tích hồi quy.
Phương pháp xử lý điểm dị biệt
Sau khi phát hiện điểm dị biệt, bước tiếp theo là quyết định cách xử lý. Đây là quá trình gồm ba giai đoạn:
Giai đoạn 1: Xác định nguyên nhân
Trước khi xử lý, cần xác định lý do xuất hiện điểm dị biệt:
- Lỗi nhập liệu: Kiểm tra xem có phải do sai sót trong quá trình thu thập hoặc nhập dữ liệu
- Đặc điểm thực tế: Có thể là phản ánh đúng hiện thực (người giàu có trong khảo sát thu nhập)
- Lỗi đo lường: Công cụ đo lường hoặc phương pháp khảo sát có vấn đề
- Sự kiện đặc biệt: Các yếu tố bên ngoài ảnh hưởng (khủng hoảng, dịch bệnh)
Giai đoạn 2: Áp dụng phương pháp xử lý
Có 4 cách chính để xử lý điểm dị biệt trong thực hành kinh tế lượng:
Cách 1: Xóa giá trị dị biệt
Khi nào sử dụng: Nếu chỉ có một vài điểm dị biệt và chắc chắn chúng do lỗi. Các điểm này sẽ nhận giá trị trống (missing).
Lưu ý: Cần cân nhắc kỹ vì có thể mất thông tin quan trọng.
Cách 2: Xóa biến
Áp dụng khi:
- Câu hỏi thiết kế chưa phù hợp
- Có quá nhiều điểm dị biệt trong biến
- Biến không cần thiết cho phân tích
- Phương pháp biến đổi biến không hiệu quả
Cách 3: Thay đổi (transform) giá trị
Phương pháp điều chỉnh giá trị cụ thể:
Ví dụ thực tế: Nếu có thang điểm 100, và có 2 điểm dị biệt là 95 và 96, trong khi giá trị cao kế tiếp là 89, có thể thay đổi 95 và 96 thành 89 hoặc 90 (89 + 1).
Cách 4: Biến đổi biến
Thay vì thay đổi từng giá trị, có thể biến đổi toàn bộ biến để tạo phân phối chuẩn:
- Logarithm transformation: log(x) – phù hợp với dữ liệu skew dương
- Square root transformation: √x – giảm độ lệch nhẹ
- Box-Cox transformation: Tối ưu hóa tham số λ
- Winsorizing: Thay thế percentile cực trị
Giai đoạn 3: Kiểm tra lại
Sau khi xử lý, cần kiểm tra lại để xác định:
Hiệu ứng domino: Việc loại bỏ điểm dị biệt có thể tạo ra điểm dị biệt mới. Nếu xuất hiện điểm dị biệt mới, cần lặp lại quá trình kiểm tra và xử lý.
Lưu ý quan trọng khi xử lý điểm dị biệt
Nguyên tắc cơ bản
- Minh bạch: Luôn báo cáo về việc phát hiện và xử lý điểm dị biệt
- Có căn cứ: Mọi quyết định xử lý phải có lý do thuyết phục
- So sánh kết quả: Chạy phân tích cả với và không có điểm dị biệt
- Xem xét bối cảnh: Điểm dị biệt có thể chứa thông tin quan trọng
Các lỗi thường gặp
Những sai lầm cần tránh:
- Xóa điểm dị biệt chỉ vì chúng làm kết quả “xấu đi”
- Không kiểm tra nguyên nhân trước khi xử lý
- Áp dụng cùng một phương pháp cho mọi trường hợp
- Không báo cáo về việc xử lý điểm dị biệt
Ứng dụng trong nghiên cứu kinh tế Việt Nam
Nghiên cứu thu nhập hộ gia đình
Trong khảo sát thu nhập, thường xuất hiện:
- Hộ gia đình có thu nhập rất cao (doanh nhân, nghệ sĩ)
- Hộ nghèo có thu nhập bất thường thấp
- Thu nhập tăng đột biến do thưởng Tết, bán tài sản
Nghiên cứu giáo dục
Điểm dị biệt trong giáo dục có thể là:
- Học sinh xuất sắc có điểm cao bất thường
- Trường học ở vùng khó khăn có kết quả đặc biệt
- Ảnh hưởng của các chương trình hỗ trợ đặc biệt
Tổng kết
Phát hiện và xử lý điểm dị biệt là kỹ năng quan trọng trong thực hành kinh tế lượng. SPSS cung cấp công cụ mạnh mẽ thông qua chức năng Explore, cho phép:
Những điều quan trọng cần nhớ:
- Điểm dị biệt không phải lúc nào cũng là “lỗi” cần loại bỏ
- Cần hiểu nguyên nhân trước khi quyết định xử lý
- Sử dụng boxplot để trực quan hóa hiệu quả
- Luôn báo cáo minh bạch về quá trình xử lý
- Kết hợp nhiều phương pháp để có cái nhìn toàn diện
Việc thành thạo các kỹ thuật này sẽ giúp các bạn sinh viên và nhà nghiên cứu tạo ra những phân tích kinh tế lượng chất lượng cao, phù hợp với đặc điểm của dữ liệu Việt Nam và đáp ứng các tiêu chuẩn nghiên cứu quốc tế.
Key Points:
- Điểm dị biệt có thể là thông tin quan trọng hoặc nhiễu cần loại bỏ
- SPSS Explore cung cấp công cụ toàn diện để phát hiện outliers
- Boxplot là công cụ trực quan hiệu quả nhất cho outlier detection
- Có bốn phương pháp chính để xử lý: xóa giá trị, xóa biến, transform giá trị, transform biến
- Luôn kiểm tra lại sau khi xử lý để tránh tạo ra outlier mới
- Cần báo cáo minh bạch về quá trình phát hiện và xử lý outliers
Xem thêm: Các khuyết tật của dữ liệu trong hồi quy OLS
Phụ lục – Code cho các phần mềm khác
SPSS Syntax
SPSS Syntax (.sps)
* Phát hiện và xử lý điểm dị biệt trong SPSS
* Tác giả: Thực hành kinh tế lượng
* Mục đích: Phát hiện outliers univariate và multivariate
* Mở file dữ liệu
GET FILE='/data/2-way-anova.sav'.
* Phát hiện điểm dị biệt univariate cho tất cả biến liên tục
EXAMINE VARIABLES=system1 system2 system3
/PLOT BOXPLOT HISTOGRAM
/STATISTICS DESCRIPTIVES EXTREME(5)
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
* Phát hiện điểm dị biệt theo nhóm (ví dụ theo giới tính)
EXAMINE VARIABLES=system1 BY sex
/PLOT BOXPLOT HISTOGRAM
/STATISTICS DESCRIPTIVES EXTREME(5)
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
* Tính toán thủ công các ngưỡng outlier
FREQUENCIES VARIABLES=system1
/STATISTICS=STDDEV VARIANCE RANGE MINIMUM MAXIMUM SEMEAN MEAN MEDIAN MODE
/PERCENTILES=25.0 50.0 75.0
/ORDER=ANALYSIS.
* Tạo biến đánh dấu outliers
COMPUTE Q1 = 25.
COMPUTE Q3 = 75.
COMPUTE IQR = Q3 - Q1.
COMPUTE Lower_Fence = Q1 - 1.5 * IQR.
COMPUTE Upper_Fence = Q3 + 1.5 * IQR.
COMPUTE Extreme_Lower = Q1 - 3 * IQR.
COMPUTE Extreme_Upper = Q3 + 3 * IQR.
* Đánh dấu các loại outliers
IF (system1 < Lower_Fence OR system1 > Upper_Fence) outlier_mild = 1.
IF (system1 < Extreme_Lower OR system1 > Extreme_Upper) outlier_extreme = 1.
* Xử lý outliers bằng cách winsorizing
COMPUTE system1_winsor = system1.
IF (system1 > Upper_Fence) system1_winsor = Upper_Fence.
IF (system1 < Lower_Fence) system1_winsor = Lower_Fence.
* Transform biến để giảm outliers
COMPUTE system1_log = LG10(system1).
COMPUTE system1_sqrt = SQRT(system1).
* So sánh trước và sau xử lý
EXAMINE VARIABLES=system1 system1_winsor system1_log
/PLOT BOXPLOT
/STATISTICS DESCRIPTIVES
/NOTOTAL.
Stata
Stata (.do file)
* Phát hiện và xử lý điểm dị biệt trong Stata
* Tác giả: Thực hành kinh tế lượng
* Mục đích: Comprehensive outlier detection và treatment
* Mở file dữ liệu
use "2-way-anova.dta", clear
* Mô tả dữ liệu cơ bản
describe system1 system2 system3
summarize system1 system2 system3, detail
* Phát hiện outliers bằng IQR method
foreach var of varlist system1 system2 system3 {
quietly summarize `var', detail
scalar q1_`var' = r(p25)
scalar q3_`var' = r(p75)
scalar iqr_`var' = q3_`var' - q1_`var'
scalar lower_fence_`var' = q1_`var' - 1.5 * iqr_`var'
scalar upper_fence_`var' = q3_`var' + 1.5 * iqr_`var'
scalar extreme_lower_`var' = q1_`var' - 3 * iqr_`var'
scalar extreme_upper_`var' = q3_`var' + 3 * iqr_`var'
* Tạo biến đánh dấu outliers
generate outlier_mild_`var' = (`var' < lower_fence_`var') | (`var' > upper_fence_`var')
generate outlier_extreme_`var' = (`var' < extreme_lower_`var') | (`var' > extreme_upper_`var')
* Liệt kê các outliers
list id `var' if outlier_extreme_`var' == 1
}
* Tạo boxplot để visualize outliers
graph box system1, over(sex) title("Boxplot of system1 by gender") ///
note("Outliers are shown as dots beyond whiskers")
* Phương pháp phát hiện outliers bằng z-score
foreach var of varlist system1 system2 system3 {
egen z_`var' = std(`var')
generate outlier_z_`var' = abs(z_`var') > 3
tab outlier_z_`var'
}
* Xử lý outliers bằng winsorizing
foreach var of varlist system1 system2 system3 {
egen p1_`var' = pctile(`var'), p(1)
egen p99_`var' = pctile(`var'), p(99)
generate `var'_winsor = `var'
replace `var'_winsor = p1_`var' if `var' < p1_`var' replace `var'_winsor = p99_`var' if `var' > p99_`var'
}
* Transform biến để giảm skewness và outliers
generate system1_log = log(system1) if system1 > 0
generate system1_sqrt = sqrt(system1) if system1 >= 0
generate system1_inv = 1/system1 if system1 != 0
* So sánh phân phối trước và sau xử lý
histogram system1, normal title("Original distribution")
histogram system1_winsor, normal title("Winsorized distribution")
histogram system1_log, normal title("Log transformed distribution")
* Kiểm tra multivariate outliers bằng Mahalanobis distance
reg system1 system2 system3
predict mahal, mahalanobis
generate outlier_mahal = mahal > invchi2(3, 0.001)
list id system1 system2 system3 mahal if outlier_mahal == 1
* Tạo báo cáo tổng hợp
tabstat system1 system1_winsor system1_log, ///
statistics(n mean sd min max p25 p50 p75 skew kurt) ///
columns(statistics) format(%9.3f)
R
R (.R script)
# Phát hiện và xử lý điểm dị biệt trong R
# Tác giả: Thực hành kinh tế lượng
# Mục đích: Comprehensive outlier detection và visualization
# Tải thư viện cần thiết
library(haven) # Đọc file SPSS
library(ggplot2) # Visualization
library(dplyr) # Data manipulation
library(VIM) # Visualization and Imputation of Missing values
library(car) # Companion to Applied Regression
library(outliers) # Outlier detection tests
library(robustbase) # Robust statistics
# Đọc dữ liệu
data <- read_sav("2-way-anova.sav")
# Chọn các biến liên tục
numeric_vars <- c("system1", "system2", "system3")
# Hàm phát hiện outliers bằng IQR method
detect_outliers_iqr <- function(x, k = 1.5) {
q1 <- quantile(x, 0.25, na.rm = TRUE)
q3 <- quantile(x, 0.75, na.rm = TRUE)
iqr <- q3 - q1
lower_fence <- q1 - k * iqr
upper_fence <- q3 + k * iqr
return(list(
outliers = which(x < lower_fence | x > upper_fence),
lower_fence = lower_fence,
upper_fence = upper_fence,
mild_outliers = which(x < (q1 - 1.5*iqr) | x > (q3 + 1.5*iqr)),
extreme_outliers = which(x < (q1 - 3*iqr) | x > (q3 + 3*iqr))
))
}
# Phát hiện outliers cho từng biến
outlier_results <- list()
for(var in numeric_vars) {
cat("\\nAnalyzing outliers for:", var, "\\n")
outlier_results[[var]] <- detect_outliers_iqr(data[[var]]) cat("Number of mild outliers:", length(outlier_results[[var]]$mild_outliers), "\\n") cat("Number of extreme outliers:", length(outlier_results[[var]]$extreme_outliers), "\\n") # In ra các extreme outliers if(length(outlier_results[[var]]$extreme_outliers) > 0) {
cat("Extreme outlier values:\\n")
print(data[[var]][outlier_results[[var]]$extreme_outliers])
}
}
# Tạo boxplot cho tất cả biến
data_long <- data %>%
select(all_of(numeric_vars)) %>%
tidyr::pivot_longer(everything(), names_to = "variable", values_to = "value")
ggplot(data_long, aes(x = variable, y = value)) +
geom_boxplot(outlier.colour = "red", outlier.size = 2) +
labs(title = "Boxplot của các biến - Phát hiện điểm dị biệt",
x = "Biến", y = "Giá trị") +
theme_minimal()
# Phân tích outliers theo nhóm (ví dụ theo sex)
if("sex" %in% names(data)) {
ggplot(data, aes(x = factor(sex), y = system1)) +
geom_boxplot(aes(fill = factor(sex)), outlier.colour = "red") +
labs(title = "Boxplot system1 theo giới tính",
x = "Giới tính", y = "System1") +
scale_fill_discrete(name = "Giới tính", labels = c("Nam", "Nữ")) +
theme_minimal()
}
# Phát hiện outliers bằng z-score
detect_outliers_zscore <- function(x, threshold = 3) {
z_scores <- abs(scale(x)) return(which(z_scores > threshold))
}
# Áp dụng z-score method
for(var in numeric_vars) {
z_outliers <- detect_outliers_zscore(data[[var]])
cat("Z-score outliers for", var, ":", length(z_outliers), "\\n")
}
# Xử lý outliers bằng winsorizing
winsorize <- function(x, probs = c(0.01, 0.99)) {
quantiles <- quantile(x, probs = probs, na.rm = TRUE)
x[x < quantiles[1]] <- quantiles[1] x[x > quantiles[2]] <- quantiles[2]
return(x)
}
# Áp dụng winsorizing
data_winsor <- data
for(var in numeric_vars) {
data_winsor[[paste0(var, "_winsor")]] <- winsorize(data[[var]]) } # Transform để giảm skewness for(var in numeric_vars) { # Log transformation (chỉ khi tất cả giá trị > 0)
if(all(data[[var]] > 0, na.rm = TRUE)) {
data[[paste0(var, "_log")]] <- log(data[[var]]) } # Square root transformation (chỉ khi tất cả giá trị >= 0)
if(all(data[[var]] >= 0, na.rm = TRUE)) {
data[[paste0(var, "_sqrt")]] <- sqrt(data[[var]]) } } # Phát hiện multivariate outliers bằng Mahalanobis distance if(length(numeric_vars) > 1) {
# Loại bỏ missing values
complete_data <- data[complete.cases(data[numeric_vars]), numeric_vars] if(nrow(complete_data) > 0) {
# Tính Mahalanobis distance
center <- colMeans(complete_data)
cov_matrix <- cov(complete_data)
mahal_dist <- mahalanobis(complete_data, center, cov_matrix)
# Xác định outliers (sử dụng chi-square distribution)
cutoff <- qchisq(0.999, df = length(numeric_vars))
multivar_outliers <- which(mahal_dist > cutoff)
cat("\\nMultivariate outliers:", length(multivar_outliers), "\\n")
if(length(multivar_outliers) > 0) {
cat("Outlier indices:", multivar_outliers, "\\n")
}
}
}
# So sánh thống kê mô tả trước và sau xử lý
comparison_stats <- function(original, processed, var_name) {
stats_orig <- c(
mean = mean(original, na.rm = TRUE),
median = median(original, na.rm = TRUE),
sd = sd(original, na.rm = TRUE),
skewness = moments::skewness(original, na.rm = TRUE),
kurtosis = moments::kurtosis(original, na.rm = TRUE)
)
stats_proc <- c(
mean = mean(processed, na.rm = TRUE),
median = median(processed, na.rm = TRUE),
sd = sd(processed, na.rm = TRUE),
skewness = moments::skewness(processed, na.rm = TRUE),
kurtosis = moments::kurtosis(processed, na.rm = TRUE)
)
comparison <- data.frame(
Statistic = names(stats_orig),
Original = round(stats_orig, 3),
Processed = round(stats_proc, 3)
)
cat("\\nComparison for", var_name, ":\\n")
print(comparison)
}
# So sánh system1 gốc vs winsorized
if("system1_winsor" %in% names(data_winsor)) {
comparison_stats(data$system1, data_winsor$system1_winsor, "System1 (Winsorized)")
}
# Tạo histogram so sánh
if("system1_winsor" %in% names(data_winsor)) {
par(mfrow = c(2, 2))
hist(data$system1, main = "Original system1", xlab = "Value", col = "lightblue")
hist(data_winsor$system1_winsor, main = "Winsorized system1", xlab = "Value", col = "lightgreen")
if("system1_log" %in% names(data)) {
hist(data$system1_log, main = "Log transformed system1", xlab = "Value", col = "lightyellow")
}
if("system1_sqrt" %in% names(data)) {
hist(data$system1_sqrt, main = "Square root transformed system1", xlab = "Value", col = "lightpink")
}
par(mfrow = c(1, 1))
}
# Kết luận và khuyến nghị
cat("\\n=== KẾT LUẬN VÀ KHUYẾN NGHỊ ===\\n")
cat("1. Luôn kiểm tra nguyên nhân của outliers trước khi xử lý\\n")
cat("2. Sử dụng multiple methods để cross-validate outlier detection\\n")
cat("3. Document tất cả các bước xử lý outliers\\n")
cat("4. So sánh kết quả analysis với và không có outliers\\n")
cat("5. Xem xét robust methods nếu có nhiều outliers\\n")
Python
Python (.py script)
# Phát hiện và xử lý điểm dị biệt trong Python
# Tác giả: Thực hành kinh tế lượng
# Mục đích: Comprehensive outlier detection và treatment
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from sklearn.preprocessing import RobustScaler
from sklearn.covariance import EllipticEnvelope
import pyreadstat
import warnings
warnings.filterwarnings('ignore')
# Thiết lập hiển thị
plt.rcParams['font.family'] = 'DejaVu Sans'
sns.set_style("whitegrid")
# Đọc dữ liệu
data, meta = pyreadstat.read_sav("2-way-anova.sav")
print("Dữ liệu đã được tải thành công!")
print(f"Kích thước dữ liệu: {data.shape}")
# Chọn các biến số
numeric_cols = ['system1', 'system2', 'system3']
numeric_data = data[numeric_cols].select_dtypes(include=[np.number])
print(f"\\nCác biến số được phân tích: {list(numeric_data.columns)}")
# Class để phát hiện outliers
class OutlierDetector:
def __init__(self, data):
self.data = data
self.outlier_indices = {}
def iqr_method(self, column, k=1.5):
"""Phát hiện outliers bằng IQR method"""
Q1 = self.data[column].quantile(0.25)
Q3 = self.data[column].quantile(0.75)
IQR = Q3 - Q1
lower_fence = Q1 - k * IQR
upper_fence = Q3 + k * IQR
outliers = self.data[(self.data[column] < lower_fence) | (self.data[column] > upper_fence)].index
# Phân loại mild và extreme outliers
extreme_lower = Q1 - 3 * IQR
extreme_upper = Q3 + 3 * IQR
extreme_outliers = self.data[(self.data[column] < extreme_lower) | (self.data[column] > extreme_upper)].index
mild_outliers = outliers.difference(extreme_outliers)
return {
'all_outliers': outliers,
'mild_outliers': mild_outliers,
'extreme_outliers': extreme_outliers,
'lower_fence': lower_fence,
'upper_fence': upper_fence,
'Q1': Q1,
'Q3': Q3,
'IQR': IQR
}
def zscore_method(self, column, threshold=3):
"""Phát hiện outliers bằng Z-score method"""
z_scores = np.abs(stats.zscore(self.data[column].dropna()))
outliers = self.data.iloc[np.where(z_scores > threshold)[0]].index
return outliers
def modified_zscore_method(self, column, threshold=3.5):
"""Phát hiện outliers bằng Modified Z-score (sử dụng median)"""
median = self.data[column].median()
mad = np.median(np.abs(self.data[column] - median))
modified_z_scores = 0.6745 * (self.data[column] - median) / mad
outliers = self.data[np.abs(modified_z_scores) > threshold].index
return outliers
# Khởi tạo detector
detector = OutlierDetector(data)
# Phân tích từng biến
outlier_summary = {}
for col in numeric_data.columns:
print(f"\\n{'='*50}")
print(f"PHÂN TÍCH OUTLIERS CHO BIẾN: {col.upper()}")
print(f"{'='*50}")
# IQR method
iqr_results = detector.iqr_method(col)
outlier_summary[col] = iqr_results
print(f"IQR Method:")
print(f" - Mild outliers: {len(iqr_results['mild_outliers'])}")
print(f" - Extreme outliers: {len(iqr_results['extreme_outliers'])}")
print(f" - Lower fence: {iqr_results['lower_fence']:.3f}")
print(f" - Upper fence: {iqr_results['upper_fence']:.3f}")
# Z-score method
zscore_outliers = detector.zscore_method(col)
print(f"\\nZ-score Method (threshold=3):")
print(f" - Outliers: {len(zscore_outliers)}")
# Modified Z-score method
mod_zscore_outliers = detector.modified_zscore_method(col)
print(f"\\nModified Z-score Method (threshold=3.5):")
print(f" - Outliers: {len(mod_zscore_outliers)}")
# Hiển thị extreme outliers
if len(iqr_results['extreme_outliers']) > 0:
print(f"\\nExtreme outlier values:")
extreme_values = data.loc[iqr_results['extreme_outliers'], col]
for idx, val in extreme_values.items():
print(f" Index {idx}: {val:.3f}")
# Visualization
def create_outlier_plots():
"""Tạo các biểu đồ phát hiện outliers"""
# Tính số lượng subplot cần thiết
n_vars = len(numeric_data.columns)
fig, axes = plt.subplots(2, n_vars, figsize=(5*n_vars, 10))
if n_vars == 1:
axes = axes.reshape(-1, 1)
for i, col in enumerate(numeric_data.columns):
# Boxplot
axes[0, i].boxplot(data[col].dropna())
axes[0, i].set_title(f'Boxplot - {col}')
axes[0, i].set_ylabel('Giá trị')
# Histogram with outliers highlighted
hist_data = data[col].dropna()
axes[1, i].hist(hist_data, bins=30, alpha=0.7, color='skyblue', edgecolor='black')
# Đánh dấu outliers
iqr_results = outlier_summary[col]
outlier_values = data.loc[iqr_results['all_outliers'], col]
for val in outlier_values:
axes[1, i].axvline(val, color='red', linestyle='--', alpha=0.7)
axes[1, i].set_title(f'Histogram với Outliers - {col}')
axes[1, i].set_xlabel('Giá trị')
axes[1, i].set_ylabel('Tần suất')
plt.tight_layout()
plt.show()
# Tạo plots
create_outlier_plots()
# Boxplot theo nhóm (nếu có biến phân loại)
if 'sex' in data.columns:
plt.figure(figsize=(12, 6))
for i, col in enumerate(numeric_data.columns[:2]): # Chỉ hiển thị 2 biến đầu
plt.subplot(1, 2, i+1)
# Tạo boxplot theo giới tính
box_data = [data[data['sex'] == 0][col].dropna(),
data[data['sex'] == 1][col].dropna()]
plt.boxplot(box_data, labels=['Nam', 'Nữ'])
plt.title(f'Boxplot {col} theo giới tính')
plt.ylabel('Giá trị')
plt.tight_layout()
plt.show()
# Xử lý outliers
class OutlierTreatment:
def __init__(self, data):
self.data = data.copy()
def winsorize(self, column, limits=(0.01, 0.01)):
"""Winsorizing - thay thế outliers bằng percentile values"""
from scipy.stats.mstats import winsorize
winsorized = winsorize(self.data[column], limits=limits)
return winsorized
def cap_outliers(self, column, lower_cap=None, upper_cap=None):
"""Capping outliers tại giá trị ngưỡng"""
result = self.data[column].copy()
if lower_cap is not None:
result = result.clip(lower=lower_cap)
if upper_cap is not None:
result = result.clip(upper=upper_cap)
return result
def remove_outliers(self, column, method='iqr', **kwargs):
"""Loại bỏ outliers"""
if method == 'iqr':
iqr_results = detector.iqr_method(column)
clean_indices = self.data.index.difference(iqr_results['all_outliers'])
return self.data.loc[clean_indices, column]
def transform_data(self, column, method='log'):
"""Transform dữ liệu để giảm skewness"""
if method == 'log':
# Chỉ áp dụng nếu tất cả giá trị > 0
if (self.data[column] > 0).all():
return np.log(self.data[column])
else:
# Log(x+1) nếu có giá trị <= 0 return np.log(self.data[column] + 1) elif method == 'sqrt': if (self.data[column] >= 0).all():
return np.sqrt(self.data[column])
elif method == 'boxcox':
# Box-Cox transformation
transformed, lambda_param = stats.boxcox(self.data[column] + 1)
print(f"Box-Cox lambda for {column}: {lambda_param:.3f}")
return transformed
# Áp dụng các phương pháp xử lý
treatment = OutlierTreatment(data)
# Tạo bảng so sánh các phương pháp
comparison_results = {}
for col in numeric_data.columns:
original = data[col]
# Winsorizing
winsorized = treatment.winsorize(col, limits=(0.01, 0.01))
# Capping (sử dụng IQR fences)
iqr_info = outlier_summary[col]
capped = treatment.cap_outliers(col,
lower_cap=iqr_info['lower_fence'],
upper_cap=iqr_info['upper_fence'])
# Log transformation
log_transformed = treatment.transform_data(col, method='log')
# So sánh thống kê
comparison_results[col] = {
'Original': {
'Mean': original.mean(),
'Median': original.median(),
'Std': original.std(),
'Skew': stats.skew(original.dropna()),
'Kurt': stats.kurtosis(original.dropna())
},
'Winsorized': {
'Mean': np.mean(winsorized),
'Median': np.median(winsorized),
'Std': np.std(winsorized),
'Skew': stats.skew(winsorized),
'Kurt': stats.kurtosis(winsorized)
},
'Capped': {
'Mean': capped.mean(),
'Median': capped.median(),
'Std': capped.std(),
'Skew': stats.skew(capped.dropna()),
'Kurt': stats.kurtosis(capped.dropna())
},
'Log_Transform': {
'Mean': log_transformed.mean(),
'Median': log_transformed.median(),
'Std': log_transformed.std(),
'Skew': stats.skew(log_transformed.dropna()),
'Kurt': stats.kurtosis(log_transformed.dropna())
}
}
# Hiển thị bảng so sánh
for col in numeric_data.columns:
print(f"\\n{'='*60}")
print(f"SO SÁNH CÁC PHƯƠNG PHÁP XỬ LÝ CHO {col.upper()}")
print(f"{'='*60}")
comparison_df = pd.DataFrame(comparison_results[col]).round(3)
print(comparison_df)
# Multivariate outlier detection
def detect_multivariate_outliers():
"""Phát hiện multivariate outliers"""
print(f"\\n{'='*60}")
print("PHÁT HIỆN MULTIVARIATE OUTLIERS")
print(f"{'='*60}")
# Loại bỏ missing values
clean_data = numeric_data.dropna()
if len(clean_data) > 0:
# Mahalanobis distance
from scipy.spatial.distance import mahalanobis
mean = clean_data.mean()
cov = clean_data.cov()
# Tính Mahalanobis distance cho từng observation
mahal_distances = []
for i, (idx, row) in enumerate(clean_data.iterrows()):
dist = mahalanobis(row, mean, np.linalg.inv(cov))
mahal_distances.append(dist)
mahal_distances = np.array(mahal_distances)
# Xác định threshold (sử dụng chi-square distribution)
threshold = stats.chi2.ppf(0.999, df=len(numeric_data.columns))
multivar_outliers = clean_data.index[mahal_distances > threshold]
print(f"Threshold (chi-square 0.999): {threshold:.3f}")
print(f"Số lượng multivariate outliers: {len(multivar_outliers)}")
if len(multivar_outliers) > 0:
print("\\nCác multivariate outliers:")
for idx in multivar_outliers:
print(f" Index {idx}: Mahalanobis distance = {mahal_distances[clean_data.index.get_loc(idx)]:.3f}")
# Visualization
if len(numeric_data.columns) >= 2:
plt.figure(figsize=(10, 6))
plt.scatter(clean_data.iloc[:, 0], clean_data.iloc[:, 1],
c=mahal_distances, cmap='viridis', alpha=0.6)
plt.colorbar(label='Mahalanobis Distance')
plt.xlabel(clean_data.columns[0])
plt.ylabel(clean_data.columns[1])
plt.title('Multivariate Outliers (Mahalanobis Distance)')
# Đánh dấu outliers
outlier_data = clean_data.loc[multivar_outliers]
plt.scatter(outlier_data.iloc[:, 0], outlier_data.iloc[:, 1],
c='red', s=100, marker='x', label='Outliers')
plt.legend()
plt.show()
# Thực hiện multivariate outlier detection
detect_multivariate_outliers()
# Tạo báo cáo tổng kết
print(f"\\n{'='*80}")
print("BÁO CÁO TỔNG KẾT OUTLIER ANALYSIS")
print(f"{'='*80}")
total_outliers = 0
for col in numeric_data.columns:
n_outliers = len(outlier_summary[col]['all_outliers'])
total_outliers += n_outliers
print(f"{col}: {n_outliers} outliers ({n_outliers/len(data)*100:.1f}% của dữ liệu)")
print(f"\\nTổng cộng: {total_outliers} outlier instances được phát hiện")
print(f"\\nKHUYẾN NGHỊ:")
print("1. Kiểm tra nguyên nhân của các extreme outliers")
print("2. Xem xét sử dụng robust statistical methods")
print("3. Document tất cả outlier treatment decisions")
print("4. Compare results với và không có outliers")
print("5. Consider domain expertise khi quyết định xử lý")
Tài liệu tham khảo
- Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics. 5th Edition. SAGE Publications.
- Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2019). Multivariate Data Analysis. 8th Edition. Cengage Learning.
- Hoaglin, D. C., & Iglewicz, B. (1987). Fine-tuning some resistant rules for outlier labeling. Journal of American Statistical Association, 82(400), 1147-1149.
- IBM Corporation. (2023). IBM SPSS Statistics Base 29.0.0 User’s Guide. IBM Corporation.
- Leys, C., Ley, C., Klein, O., Bernard, P., & Licata, L. (2013). Detecting outliers: Do not use standard deviation around the mean, use absolute deviation around the median. Journal of Experimental Social Psychology, 49(4), 764-766.
- Tabachnick, B. G., & Fidell, L. S. (2019). Using Multivariate Statistics. 7th Edition. Pearson.
- Tukey, J. W. (1977). Exploratory Data Analysis. Addison-Wesley.