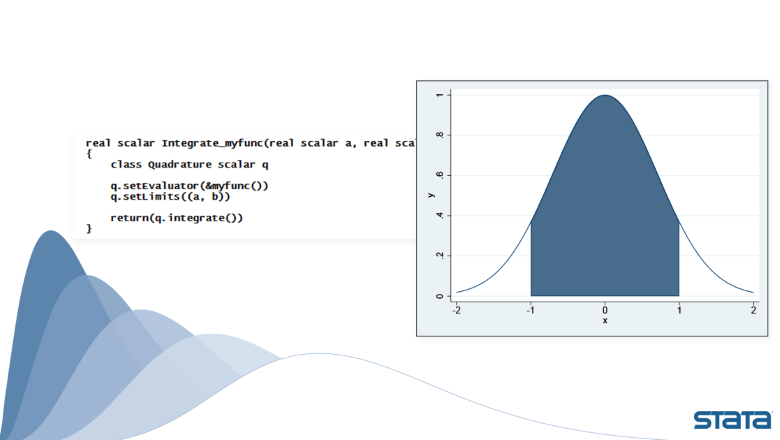
Bên cạnh lớp LinearProgram() để giải bài toán tối ưu trong quy hoạch tuyến tính hay bài toán ma trận cơ bản, công cụ Mata ở Stata còn có nhiều lớp đối tượng hữu ích khác. Một trong những lớp được sử dụng phổ biến là lớp Quadrature() được sử dụng để tính tích phân của hàm. Tối thiểu, bạn phải thiết lập cho Mata biết hàm cần lấy tích phân cũng như các cận của nó. Bạn cũng có thể thiết lập kỹ thuật lấy tích phân, số lần lặp tối đa được phép, tiêu chí hội tụ, các đối số được truyền… Tính tích phân với …