Phân phối chuẩn hóa – Normality
Kiểm tra giả định phân phối chuẩn với SPSS

Tóm tắt: Giả định phân phối chuẩn là một trong những yêu cầu cơ bản nhất trong thực hành kinh tế lượng. Bài viết này hướng dẫn chi tiết cách kiểm tra tính phân phối chuẩn của dữ liệu trên SPSS thông qua ba phương pháp chính: phân tích histogram, đánh giá các chỉ số Skewness và Kurtosis, và thực hiện các kiểm định Kolmogorov-Smirnov cùng Shapiro-Wilk. Đồng thời, bài viết cũng trình bày các phương pháp xử lý khi dữ liệu không thỏa mãn giả định này.
Giới thiệu về giả định phân phối chuẩn
Nội dung chính
- Giới thiệu về giả định phân phối chuẩn
- Bốn vấn đề cơ bản về phân phối chuẩn
- Ba phương pháp kiểm tra phân phối chuẩn trên SPSS
- Phương pháp tổng hợp đánh giá phân phối chuẩn
- Xử lý dữ liệu không có phân phối chuẩn
- Lưu ý quan trọng và cảnh báo
- Tổng kết
- Phụ lục: Code tương đương trong các phần mềm khác
- Tài liệu tham khảo
Trong thực hành kinh tế lượng, giả định phân phối chuẩn đóng vai trò then chốt trong hầu hết các phương pháp phân tích thống kê. Tầm quan trọng của giả định này xuất phát từ thực tế là đa số các kiểm định và phương pháp phân tích trong các chương trình Kinh tế lượng và Thống kê đều được xây dựng dựa trên giả định về tính phân phối chuẩn của dữ liệu.
Do đó, trong nghiên cứu thực tế, các bạn sinh viên cần thực hiện kiểm tra dữ liệu, làm sạch dữ liệu và loại bỏ ảnh hưởng của các điểm dị biệt để đưa dữ liệu về dạng chuẩn hóa phù hợp.
Ví dụ minh họa trong bối cảnh Việt Nam
Để hiểu rõ hơn về tầm quan trọng của giả định phân phối chuẩn, hãy xem xét một ví dụ cụ thể trong bối cảnh kinh tế Việt Nam. Giả sử chúng ta đang nghiên cứu về mức lương của nhân viên trong ngành công nghệ thông tin tại TP.HCM. Nếu dữ liệu lương có phân phối chuẩn, chúng ta có thể:
- Sử dụng các kiểm định t-test để so sánh lương trung bình giữa các nhóm
- Áp dụng phân tích hồi quy để xác định các yếu tố ảnh hưởng đến mức lương
- Tính toán khoảng tin cậy chính xác cho các ước lượng
- Thực hiện dự báo với độ tin cậy cao
Ngược lại, nếu dữ liệu không có phân phối chuẩn, việc áp dụng các phương pháp thống kê truyền thống có thể dẫn đến kết quả thiếu chính xác và kết luận sai lệch.
Bốn vấn đề cơ bản về phân phối chuẩn
Để nắm vững về giả định phân phối chuẩn trong thực hành kinh tế lượng, chúng ta cần tìm hiểu bốn vấn đề cơ bản sau:
- Phân phối chuẩn là gì?
- Tại sao phân phối chuẩn lại quan trọng?
- Làm thế nào để kiểm tra phân phối chuẩn?
- Xử lý như thế nào khi dữ liệu không có phân phối chuẩn?
1. Phân phối chuẩn là gì?
Phân phối chuẩn là một phân phối xác suất có dạng hình chuông đối xứng, được xác định hoàn toàn bởi hai thông số quan trọng:- Trung bình (μ – mean): Xác định vị trí trung tâm của phân phối
- Phương sai (σ² – variance): Xác định độ rộng hay độ phân tán của phân phối
Công thức của hàm mật độ xác suất phân phối chuẩn là:
$$f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2}$$
Trong đó:
- \(x\): giá trị của biến ngẫu nhiên
- \(\mu\): trung bình của phân phối
- \(\sigma\): độ lệch chuẩn của phân phối
- \(\pi\): hằng số Pi (≈ 3.14159)
- \(e\): cơ số tự nhiên (≈ 2.71828)
2. Tại sao phân phối chuẩn lại quan trọng?
Tầm quan trọng của phân phối chuẩn trong thực hành kinh tế lượng được thể hiện qua một số khía cạnh sau:
Định lý giới hạn trung tâm
Ý tưởng cốt lõi đằng sau việc suy diễn thống kê là khi cỡ mẫu càng lớn thì phân phối sẽ tiệm cận phân phối chuẩn. Đây chính là nội dung của định lý giới hạn trung tâm.
Phân loại kiểm định thống kê
Đa phần các kiểm định thống kê được chia thành hai nhóm chính:
- Kiểm định tham số (parametric tests): Dựa trên giả định rằng dữ liệu có phân phối chuẩn
- Kiểm định phi tham số (non-parametric tests): Không dựa trên giả định về sự chuẩn hóa của dữ liệu
Hiệu quả của kiểm định
Một điểm quan trọng cần lưu ý là kiểm định phi tham số thường ít hiệu quả (less powerful) hơn so với các kiểm định tham số. Điều này có nghĩa là:
- Kiểm định phi tham số có khả năng phát hiện sự khác biệt thực tế thấp hơn
- Xác suất mắc lỗi loại 2 (Type II) (không phát hiện được sự khác biệt khi nó thực sự tồn tại) cao hơn
- Khoảng tin cậy thường rộng hơn, do đó ít chính xác hơn
Chính vì vậy, trong thực hành kinh tế lượng, chúng ta luôn mong muốn thực hiện các kiểm định tham số để gia tăng cơ hội phát hiện những kết quả có ý nghĩa thống kê.
Ba phương pháp kiểm tra phân phối chuẩn trên SPSS
Trong SPSS, có ba cách chính để xác định tính chuẩn hóa của dữ liệu. Mỗi phương pháp có những ưu điểm và hạn chế riêng, do đó việc kết hợp cả ba phương pháp sẽ cho kết quả đánh giá chính xác nhất.
Tải về dữ liệu mẫuPhương pháp 1: Phân tích histogram với đường cong chuẩn
Đây là phương pháp trực quan nhất để đánh giá tính phân phối chuẩn của dữ liệu. Histogram với đường bao là đường cong chuẩn hóa cho phép chúng ta quan sát trực tiếp hình dạng phân phối.
Hướng dẫn thực hiện trong SPSS:
- Chọn Analyze → Descriptive Statistics → Frequencies
- Chuyển các biến liên tục cần phân tích vào cửa sổ Variable(s)
- Bấm Charts, và chọn Histogram, with normal curve
- Bấm OK
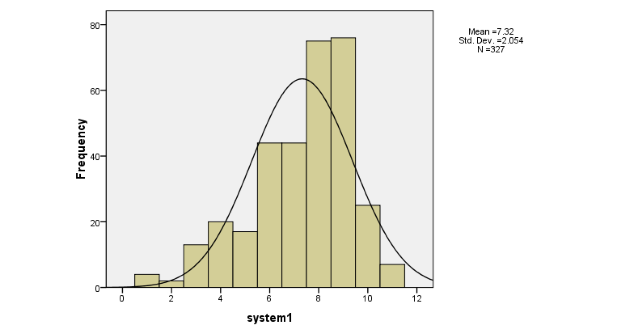
Cách diễn giải kết quả:
- Hình dạng chuông: Phân phối chuẩn có dạng hình chuông đối xứng
- Đỉnh duy nhất: Chỉ có một đỉnh ở giữa phân phối
- Đối xứng: Hai nửa của phân phối phải đối xứng qua trung bình
- Đuôi tiệm cận: Hai đuôi của phân phối tiệm cận về không
Phương pháp 2: Đánh giá qua chỉ số Skewness và Kurtosis
Phương pháp này sử dụng hai chỉ số thống kê quan trọng để đánh giá tính chuẩn hóa:
Độ trôi (Skewness)
Độ trôi liên quan đến tính đối xứng của phân phối. Phân phối chuẩn là phân phối có dạng đối xứng hoàn hảo với giá trị độ trôi bằng 0.Công thức tính độ trôi:
$$skewness = \frac{\sum_{i=1}^{N}(Y_{i} – \bar{Y})^{3}}{(N-1)s^{3}}$$
Trong đó:
- \(Y_i\): giá trị quan sát thứ i của biến Y
- \(\bar{Y}\): giá trị trung bình của biến Y
- \(s\): độ lệch chuẩn của biến Y
- \(N\): kích thước mẫu
Cách diễn giải:
- Skewness = 0: Phân phối đối xứng hoàn hảo
- Skewness > 0: Phân phối lệch phải (đuôi dài bên phải)
- Skewness < 0: Phân phối lệch trái (đuôi dài bên trái)
Độ nhọn (Kurtosis)
Độ nhọn liên quan đến chóp đỉnh của phân phối. Phân phối chuẩn có chóp đỉnh cong dạng hình chuông, không quá nhọn hoặc quá phẳng.Công thức tính độ nhọn:
$$kurtosis = \frac{\sum_{i=1}^{N}(Y_{i} – \bar{Y})^{4}}{(N-1)s^{4}}$$
Tuy nhiên, trong hầu hết các phần mềm thống kê, để dễ nhớ, người ta sử dụng công thức điều chỉnh:
$$kurtosis = \frac{\sum_{i=1}^{N}(Y_{i} – \bar{Y})^{4}}{(N-1)s^{4}} – 3$$
Cách diễn giải:
- Kurtosis = 0: Phân phối chuẩn (mesokurtic)
- Kurtosis > 0: Phân phối có đỉnh nhọn (leptokurtic)
- Kurtosis < 0: Phân phối có đỉnh phẳng (platykurtic)
Hướng dẫn thực hiện trong SPSS:
- Chọn Analyze → Descriptive Statistics → Explore
- Chuyển các biến cần phân tích vào cửa sổ Dependent List
- Bấm Plots, bỏ chọn Stem-and-leaf
- Bấm OK
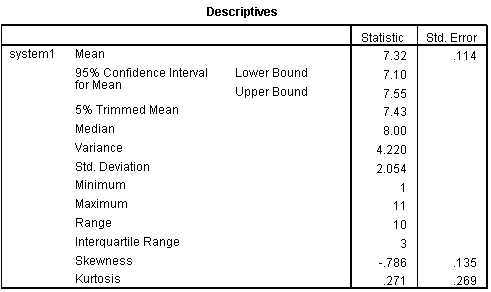
Cách diễn giải kết quả:
- Giá trị gần 0: Skewness và Kurtosis tiến gần về 0 là dấu hiệu tốt
- Khoảng tin cậy: Có thể dựa vào khoảng tin cậy (giá trị ± sai số chuẩn) để kiểm tra
- Chứa giá trị 0: Nếu khoảng tin cậy chứa giá trị 0 thì có thể xem phân phối gần chuẩn
Phương pháp 3: Kiểm định Kolmogorov-Smirnov và Shapiro-Wilk
Đây là phương pháp chính thức và có tính khách quan nhất để kiểm tra giả định phân phối chuẩn trong thực hành kinh tế lượng.
Hướng dẫn thực hiện trong SPSS:
- Chọn Analyze → Descriptive Statistics → Explore
- Chuyển các biến liên tục cần phân tích vào cửa sổ Dependent List
- Bấm Plots, bỏ chọn Stem-and-leaf, và chọn Normality plots with tests
- Bấm OK

Cách diễn giải kết quả:
Bảng Tests of Normality hiển thị kết quả của cả hai kiểm định:
- H₀: Dữ liệu có phân phối chuẩn
- H₁: Dữ liệu không có phân phối chuẩn
- p-value > 0.05: Không bác bỏ H0 (dữ liệu có phân phối chuẩn)
- p-value ≤ 0.05: Bác bỏ H0 (dữ liệu không có phân phối chuẩn)
So sánh giữa hai kiểm định:
- Shapiro-Wilk (S-W): Phù hợp với cỡ mẫu nhỏ hơn, nhưng không hiệu quả khi có nhiều giá trị trùng lặp
- Kolmogorov-Smirnov (K-S): Phù hợp với cỡ mẫu lớn hơn
Biểu đồ Q-Q Plot
Cùng với kết quả kiểm định, SPSS cũng tạo ra biểu đồ Normal Q-Q Plot để đánh giá trực quan:
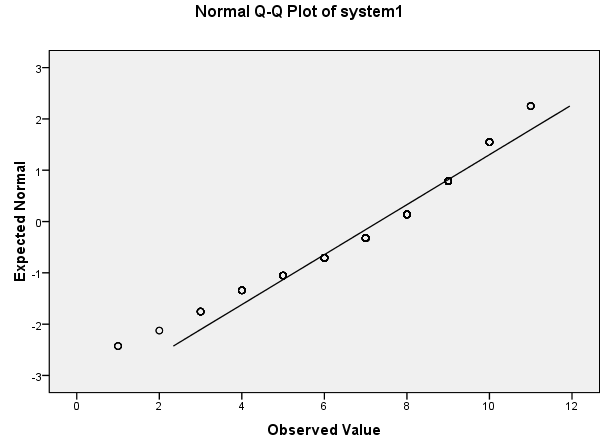
Cách diễn giải Q-Q Plot:
- Đường thẳng đen: Đại diện cho phân phối chuẩn lý thuyết
- Các điểm: Đại diện cho dữ liệu thực tế
- Nằm trên đường thẳng: Dữ liệu có phân phối chuẩn
- Phân tán xa đường thẳng: Dữ liệu không có phân phối chuẩn
Phương pháp tổng hợp đánh giá phân phối chuẩn
KIỂM ĐỊNH PHÂN PHỐI CHUẨN
Khi xem xét giả định phân phối chuẩn trong thực hành kinh tế lượng, cần kết hợp tất cả các dấu hiệu từ:
- Thống kê mô tả và đồ thị Histogram
- Biểu đồ Q-Q Plot
- Hai chỉ số Skewness và Kurtosis
- Kết quả kiểm định K-S hoặc S-W
Việc kết hợp này giúp xác định chính xác tình trạng phân phối chuẩn và phát hiện các vấn đề cần xử lý.
Xử lý dữ liệu không có phân phối chuẩn
Khi dữ liệu không thỏa mãn giả định phân phối chuẩn, câu hỏi đầu tiên cần trả lời là: “Có thực sự cần thiết phải chuẩn hóa dữ liệu không?”
Câu trả lời phụ thuộc vào nhiều yếu tố như tầm quan trọng của nghiên cứu, thời gian có sẵn, và loại phân tích cần thực hiện. Dưới đây là năm cách tiếp cận chính:
Cách 1: Giữ nguyên dữ liệu và sử dụng kiểm định tham số
Đây là cách tiếp cận thực dụng nhất. Nhiều khi sự vi phạm nhỏ về giả định phân phối chuẩn không ảnh hưởng nghiêm trọng đến kết quả:
- Phân phối chuẩn chỉ là một giả định lý tưởng, không phải yêu cầu tuyệt đối
- Các kiểm định tham số thường có tính robust nhất định
- Vi phạm nhỏ chỉ làm giảm nhẹ độ chính xác, không làm vô hiệu kết quả
- Tiết kiệm thời gian và công sức xử lý dữ liệu
Cách 2: Sử dụng kiểm định phi tham số
Đây là lựa chọn an toàn nhất khi dữ liệu không có phân phối chuẩn. Bên cạnh mỗi kiểm định tham số đều có một kiểm định phi tham số tương đương.
Ví dụ về các cặp kiểm định tương đương:
| Kiểm định tham số | Kiểm định phi tham số |
|---|---|
| Independent t-test | Mann-Whitney U test |
| Paired t-test | Wilcoxon signed-rank test |
| One-way ANOVA | Kruskal-Wallis test |
| Pearson correlation | Spearman correlation |
Cách 3: Sử dụng kiểm định robust
Kiểm định robust là sự kết hợp tốt nhất giữa ưu điểm của kiểm định tham số (hiệu quả cao) và khả năng chống chịu với vi phạm giả định. Các phương pháp này bao gồm:- Bootstrap methods
- Trimmed means
- Winsorized statistics
- Permutation tests
Cách 4: Biến đổi dữ liệu
Sử dụng các công thức toán học để biến đổi dữ liệu về dạng gần phân phối chuẩn hơn. Các phương pháp phổ biến bao gồm:
- Logarithm transformation: \(y’ = \ln(y)\) hoặc \(y’ = \log_{10}(y)\)
- Square root transformation: \(y’ = \sqrt{y}\)
- Reciprocal transformation: \(y’ = \frac{1}{y}\)
- Box-Cox transformation: Tìm λ tối ưu cho \(y’ = \frac{y^λ – 1}{λ}\)
Cách 5: Tạo biến mới từ biến cũ
Đây là cách tiếp cận phổ biến nhất trên SPSS. Sử dụng công cụ tạo biến mới để biến đổi dữ liệu:
Hướng dẫn thực hiện:
- Chọn Transform → Compute Variable
- Nhập tên cho biến mới trong ô Target Variable
- Chọn công thức biến đổi từ danh sách Functions
- Chuyển biến gốc vào vùng có dấu hỏi ?
- Bấm OK
Biến mới sẽ xuất hiện ở cột cuối cùng trong Data View. Sau đó, thực hiện lại kiểm tra tính phân phối chuẩn cho biến mới.
Lựa chọn phương pháp phù hợp
Việc lựa chọn phương pháp xử lý phụ thuộc vào:
- Mục đích nghiên cứu: Tiểu luận, luận văn, hay bài báo khoa học
- Thời gian có sẵn: Biến đổi dữ liệu tốn nhiều thời gian
- Mức độ vi phạm: Vi phạm nhỏ có thể chấp nhận được
- Kích thước mẫu: Mẫu lớn ít nhạy cảm với vi phạm giả định
- Yêu cầu về độ chính xác: Nghiên cứu quan trọng cần độ chính xác cao
Lưu ý quan trọng và cảnh báo
Khi thực hiện kiểm tra giả định phân phối chuẩn trong thực hành kinh tế lượng, cần lưu ý những điểm sau:
Về phương pháp kiểm tra
Về kích thước mẫu
- Mẫu nhỏ (n < 30): Khó đánh giá chính xác, nên sử dụng Shapiro-Wilk
- Mẫu trung bình (30 ≤ n ≤ 50): Có thể sử dụng cả hai kiểm định
- Mẫu lớn (n > 50): Kiểm định thống kê trở nên quá nhạy cảm
- Mẫu rất lớn (n > 200): Nên tập trung vào phân tích đồ thị
Về diễn giải kết quả
- Chỉ dựa vào p-value mà không xem xét biểu đồ
- Áp dụng cứng nhắc ngưỡng 0.05 cho mọi trường hợp
- Không xem xét bối cảnh và mục đích nghiên cứu
- Quên rằng phân phối chuẩn là giả định lý tưởng
Tổng kết
Giả định phân phối chuẩn là nền tảng của hầu hết các phương pháp trong thực hành kinh tế lượng. Tuy nhiên, trong thực tế, ít có dữ liệu nào thỏa mãn hoàn toàn giả định này. Điều quan trọng là hiểu rõ:
Đầu tiên, phân phối chuẩn là một giả định lý tưởng, không phải yêu cầu tuyệt đối. Sự vi phạm nhỏ về giả định này thường có thể chấp nhận được và không làm vô hiệu kết quả phân tích.
Thứ hai, việc kiểm tra giả định phân phối chuẩn cần được thực hiện một cách toàn diện, kết hợp cả phương pháp trực quan (histogram, Q-Q plot) và kiểm định thống kê (K-S, Shapiro-Wilk), cùng với việc đánh giá các chỉ số Skewness và Kurtosis.
Thứ ba, khi dữ liệu không thỏa mãn giả định phân phối chuẩn, chúng ta có nhiều lựa chọn xử lý, từ việc chấp nhận sử dụng kiểm định tham số với độ chính xác hơi giảm, đến việc sử dụng kiểm định phi tham số hoặc biến đổi dữ liệu.
Cuối cùng, quyết định về phương pháp xử lý cần cân nhắc nhiều yếu tố như mục đích nghiên cứu, thời gian có sẵn, kích thước mẫu, và mức độ vi phạm giả định.
Điểm chính cần nhớ:
- Phân phối chuẩn là giả định nền tảng của hầu hết kiểm định tham số
- Cần kết hợp cả ba phương pháp: histogram, Skewness/Kurtosis, và kiểm định thống kê
- Kiểm định K-S và S-W chỉ nên sử dụng cho mẫu nhỏ (n ≤ 50)
- Sự vi phạm nhỏ về giả định phân phối chuẩn có thể chấp nhận được
- Có nhiều phương pháp xử lý khi dữ liệu không có phân phối chuẩn
- Quyết định xử lý cần cân nhắc bối cảnh nghiên cứu cụ thể
Phụ lục: Code tương đương trong các phần mềm khác
Để hỗ trợ các bạn làm quen với nhiều công cụ phân tích khác nhau trong thực hành kinh tế lượng, phần này cung cấp code tương đương cho việc kiểm tra giả định phân phối chuẩn trong SPSS Syntax, Stata, R và Python.

SPSS Syntax
SPSS Syntax (.sps)
* Kiểm tra giả định phân phối chuẩn trong SPSS
* Giả sử biến cần kiểm tra là 'income' (thu nhập)
* Phương pháp 1: Tạo histogram với đường cong chuẩn
FREQUENCIES VARIABLES=income
/FORMAT=NOTABLE
/HISTOGRAM=NORMAL
/ORDER=ANALYSIS.
* Phương pháp 2: Tính toán Skewness và Kurtosis
DESCRIPTIVES VARIABLES=income
/STATISTICS=MEAN STDDEV VARIANCE SKEWNESS KURTOSIS.
* Phương pháp 3: Kiểm định K-S và Shapiro-Wilk
EXAMINE VARIABLES=income
/PLOT=HISTOGRAM NPPLOT
/STATISTICS=DESCRIPTIVES
/CINTERVAL=95
/MISSING=LISTWISE
/NOTOTAL.
* Phương pháp 4: Kiểm tra chi tiết với Q-Q plot
PPLOT
/VARIABLES=income
/NOLOG
/NOSTANDARDIZE
/TYPE=Q-Q
/FRACTION=BLOM
/TIES=MEAN
/DIST=NORMAL.
* Ví dụ biến đổi dữ liệu nếu không có phân phối chuẩn
* Biến đổi logarithm
COMPUTE income_log = LN(income).
EXECUTE.
* Biến đổi căn bậc hai
COMPUTE income_sqrt = SQRT(income).
EXECUTE.
* Biến đổi nghịch đảo
COMPUTE income_reciprocal = 1/income.
EXECUTE.
* Kiểm tra lại phân phối chuẩn sau biến đổi
EXAMINE VARIABLES=income_log income_sqrt income_reciprocal
/PLOT=HISTOGRAM NPPLOT
/STATISTICS=DESCRIPTIVES
/CINTERVAL=95
/MISSING=LISTWISE
/NOTOTAL.
Stata
Stata (.do)
* Kiểm tra giả định phân phối chuẩn trong Stata
* Giả sử biến cần kiểm tra là 'income' (thu nhập)
* Mở dữ liệu
use "data.dta", clear
* Phương pháp 1: Tạo histogram với đường cong chuẩn
histogram income, normal ///
title("Histogram của thu nhập với đường cong chuẩn") ///
xtitle("Thu nhập") ytitle("Mật độ") ///
scheme(s1mono)
* Phương pháp 2: Tính toán thống kê mô tả
summarize income, detail
* Tính toán Skewness và Kurtosis chi tiết
sktest income
* Phương pháp 3: Kiểm định Shapiro-Wilk
swilk income
* Kiểm định Kolmogorov-Smirnov
ksmirnov income = normal((income-r(mean))/r(sd))
* Tạo Q-Q plot
qnorm income, ///
title("Q-Q Plot cho thu nhập") ///
ytitle("Phân vị mẫu") xtitle("Phân vị lý thuyết")
* P-P plot
pnorm income, ///
title("P-P Plot cho thu nhập")
* Kiểm định Jarque-Bera
jb income
* Ví dụ biến đổi dữ liệu nếu không có phân phối chuẩn
* Biến đổi logarithm
generate income_log = ln(income)
label variable income_log "Log của thu nhập"
* Biến đổi căn bậc hai
generate income_sqrt = sqrt(income)
label variable income_sqrt "Căn bậc hai của thu nhập"
* Biến đổi nghịch đảo
generate income_reciprocal = 1/income
label variable income_reciprocal "Nghịch đảo của thu nhập"
* Biến đổi Box-Cox
gladder income
* Kiểm tra lại phân phối chuẩn sau biến đổi
foreach var of varlist income_log income_sqrt income_reciprocal {
display "Kiểm tra phân phối chuẩn cho `var'"
swilk `var'
sktest `var'
histogram `var', normal title("Histogram của `var'")
}
* So sánh các phương pháp biến đổi
graph combine ///
(histogram income, normal title("Gốc")) ///
(histogram income_log, normal title("Log")) ///
(histogram income_sqrt, normal title("Sqrt")) ///
(histogram income_reciprocal, normal title("Reciprocal")), ///
title("So sánh các phương pháp biến đổi")
R
R (.R)
# Kiểm tra giả định phân phối chuẩn trong R
# Cài đặt và tải các package cần thiết
if (!require(car)) install.packages("car")
if (!require(nortest)) install.packages("nortest")
if (!require(moments)) install.packages("moments")
if (!require(ggplot2)) install.packages("ggplot2")
if (!require(gridExtra)) install.packages("gridExtra")
library(car)
library(nortest)
library(moments)
library(ggplot2)
library(gridExtra)
# Giả sử có dữ liệu thu nhập
# Tạo dữ liệu mẫu cho ví dụ
set.seed(123)
income <- c(rnorm(150, 50000, 15000), rexp(50, 1/30000))
# Phương pháp 1: Tạo histogram với đường cong chuẩn
hist(income,
probability = TRUE,
main = "Histogram của thu nhập với đường cong chuẩn",
xlab = "Thu nhập",
ylab = "Mật độ",
col = "lightblue",
border = "black")
# Thêm đường cong chuẩn
curve(dnorm(x, mean = mean(income), sd = sd(income)),
add = TRUE,
col = "red",
lwd = 2)
# Sử dụng ggplot2 để tạo biểu đồ đẹp hơn
df <- data.frame(income = income)
p1 <- ggplot(df, aes(x = income)) +
geom_histogram(aes(y = ..density..), bins = 30, alpha = 0.7, fill = "lightblue") +
stat_function(fun = dnorm,
args = list(mean = mean(income), sd = sd(income)),
color = "red", size = 1) +
labs(title = "Histogram với đường cong chuẩn", x = "Thu nhập", y = "Mật độ")
# Phương pháp 2: Tính toán Skewness và Kurtosis
cat("Thống kê mô tả:\n")
cat("Trung bình:", mean(income), "\n")
cat("Độ lệch chuẩn:", sd(income), "\n")
cat("Skewness:", skewness(income), "\n")
cat("Kurtosis:", kurtosis(income), "\n")
# Phương pháp 3: Các kiểm định phân phối chuẩn
cat("\nKiểm định Shapiro-Wilk:\n")
shapiro_test <- shapiro.test(income)
print(shapiro_test)
cat("\nKiểm định Kolmogorov-Smirnov:\n")
ks_test <- ks.test(income, "pnorm", mean = mean(income), sd = sd(income))
print(ks_test)
cat("\nKiểm định Anderson-Darling:\n")
ad_test <- ad.test(income)
print(ad_test)
cat("\nKiểm định Jarque-Bera:\n")
jb_test <- jarque.test(income)
print(jb_test)
# Tạo Q-Q plot
p2 <- ggplot(df, aes(sample = income)) +
stat_qq() +
stat_qq_line(color = "red") +
labs(title = "Q-Q Plot", x = "Phân vị lý thuyết", y = "Phân vị mẫu")
# P-P plot
p_values <- pnorm(sort(income), mean = mean(income), sd = sd(income))
theoretical_p <- (1:length(income)) / length(income)
pp_data <- data.frame(theoretical = theoretical_p, observed = p_values)
p3 <- ggplot(pp_data, aes(x = theoretical, y = observed)) +
geom_point() +
geom_abline(intercept = 0, slope = 1, color = "red") +
labs(title = "P-P Plot", x = "Xác suất lý thuyết", y = "Xác suất quan sát")
# Kết hợp các biểu đồ
grid.arrange(p1, p2, p3, ncol = 2)
# Ví dụ biến đổi dữ liệu nếu không có phân phối chuẩn
# Biến đổi logarithm (chỉ với giá trị dương)
income_positive <- income[income > 0]
income_log <- log(income_positive)
# Biến đổi căn bậc hai
income_sqrt <- sqrt(income_positive)
# Biến đổi nghịch đảo
income_reciprocal <- 1/income_positive
# Biến đổi Box-Cox
library(car)
bc_result <- powerTransform(income_positive)
optimal_lambda <- bc_result$lambda
income_boxcox <- bcPower(income_positive, optimal_lambda)
# Hàm kiểm tra phân phối chuẩn
check_normality <- function(data, name) {
cat("\n", "="*50, "\n")
cat("Kiểm tra phân phối chuẩn cho:", name, "\n")
cat("="*50, "\n")
# Thống kê mô tả
cat("Skewness:", skewness(data), "\n")
cat("Kurtosis:", kurtosis(data), "\n")
# Kiểm định
if (length(data) <= 5000) {
shapiro_result <- shapiro.test(data)
cat("Shapiro-Wilk p-value:", shapiro_result$p.value, "\n")
}
ad_result <- ad.test(data)
cat("Anderson-Darling p-value:", ad_result$p.value, "\n")
jb_result <- jarque.test(data)
cat("Jarque-Bera p-value:", jb_result$p.value, "\n")
# Tạo biểu đồ
par(mfrow = c(1, 2))
hist(data, probability = TRUE, main = paste("Histogram -", name),
xlab = name, col = "lightblue")
curve(dnorm(x, mean = mean(data), sd = sd(data)), add = TRUE, col = "red", lwd = 2)
qqnorm(data, main = paste("Q-Q Plot -", name))
qqline(data, col = "red")
par(mfrow = c(1, 1))
}
# Kiểm tra tất cả các biến đổi
check_normality(income, "Thu nhập gốc")
check_normality(income_log, "Log thu nhập")
check_normality(income_sqrt, "Căn bậc hai thu nhập")
check_normality(income_reciprocal, "Nghịch đảo thu nhập")
check_normality(income_boxcox, "Box-Cox thu nhập")
# Tạo bảng tóm tắt kết quả
transformations <- c("Gốc", "Log", "Sqrt", "Reciprocal", "Box-Cox")
datasets <- list(income, income_log, income_sqrt, income_reciprocal, income_boxcox)
results_summary <- data.frame(
Transformation = transformations,
Skewness = sapply(datasets, skewness),
Kurtosis = sapply(datasets, kurtosis),
Shapiro_p = sapply(datasets, function(x) {
if (length(x) <= 5000) shapiro.test(x)$p.value else NA
}),
AD_p = sapply(datasets, function(x) ad.test(x)$p.value),
JB_p = sapply(datasets, function(x) jarque.test(x)$p.value)
)
print(results_summary)
Python
Python (.py)
# Kiểm tra giả định phân phối chuẩn trong Python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
from scipy.stats import jarque_bera, normaltest, anderson
import warnings
warnings.filterwarnings('ignore')
# Thiết lập matplotlib để hiển thị tiếng Việt
plt.rcParams['font.family'] = 'DejaVu Sans'
plt.rcParams['figure.figsize'] = (12, 8)
# Tạo dữ liệu mẫu (kết hợp phân phối chuẩn và không chuẩn)
np.random.seed(123)
income = np.concatenate([
np.random.normal(50000, 15000, 150), # Phân phối chuẩn
np.random.exponential(30000, 50) # Phân phối không chuẩn
])
# Tạo DataFrame
df = pd.DataFrame({'income': income})
print("KIỂM TRA GIẢ ĐỊNH PHÂN PHỐI CHUẨN")
print("="*60)
# Phương pháp 1: Tạo histogram với đường cong chuẩn
fig, axes = plt.subplots(2, 2, figsize=(15, 12))
# Histogram với đường cong chuẩn
axes[0, 0].hist(income, bins=30, density=True, alpha=0.7, color='lightblue', edgecolor='black')
mu, sigma = np.mean(income), np.std(income)
x = np.linspace(np.min(income), np.max(income), 100)
axes[0, 0].plot(x, stats.norm.pdf(x, mu, sigma), 'r-', linewidth=2, label='Đường cong chuẩn')
axes[0, 0].set_title('Histogram với đường cong chuẩn')
axes[0, 0].set_xlabel('Thu nhập')
axes[0, 0].set_ylabel('Mật độ')
axes[0, 0].legend()
axes[0, 0].grid(True, alpha=0.3)
# Phương pháp 2: Tính toán Skewness và Kurtosis
skewness_value = stats.skew(income)
kurtosis_value = stats.kurtosis(income)
print(f"Thống kê mô tả:")
print(f"Trung bình: {np.mean(income):.2f}")
print(f"Độ lệch chuẩn: {np.std(income):.2f}")
print(f"Skewness: {skewness_value:.4f}")
print(f"Kurtosis: {kurtosis_value:.4f}")
# Phương pháp 3: Các kiểm định phân phối chuẩn
print(f"\nCác kiểm định phân phối chuẩn:")
print("-" * 40)
# Kiểm định Shapiro-Wilk (chỉ cho mẫu nhỏ)
if len(income) <= 5000: shapiro_stat, shapiro_p = stats.shapiro(income) print(f"Shapiro-Wilk:") print(f" Statistic: {shapiro_stat:.4f}") print(f" p-value: {shapiro_p:.4f}") print(f" Kết luận: {'Phân phối chuẩn' if shapiro_p > 0.05 else 'Không phân phối chuẩn'}")
# Kiểm định Kolmogorov-Smirnov
ks_stat, ks_p = stats.kstest(income, lambda x: stats.norm.cdf(x, mu, sigma))
print(f"\nKolmogorov-Smirnov:")
print(f" Statistic: {ks_stat:.4f}")
print(f" p-value: {ks_p:.4f}")
print(f" Kết luận: {'Phân phối chuẩn' if ks_p > 0.05 else 'Không phân phối chuẩn'}")
# Kiểm định Anderson-Darling
ad_stat, ad_critical, ad_significance = anderson(income, dist='norm')
print(f"\nAnderson-Darling:")
print(f" Statistic: {ad_stat:.4f}")
for i, sl in enumerate(ad_significance):
print(f" Significance level {sl}%: {ad_critical[i]:.4f}")
# Kiểm định Jarque-Bera
jb_stat, jb_p = jarque_bera(income)
print(f"\nJarque-Bera:")
print(f" Statistic: {jb_stat:.4f}")
print(f" p-value: {jb_p:.4f}")
print(f" Kết luận: {'Phân phối chuẩn' if jb_p > 0.05 else 'Không phân phối chuẩn'}")
# Kiểm định D'Agostino-Pearson
dp_stat, dp_p = normaltest(income)
print(f"\nD'Agostino-Pearson:")
print(f" Statistic: {dp_stat:.4f}")
print(f" p-value: {dp_p:.4f}")
print(f" Kết luận: {'Phân phối chuẩn' if dp_p > 0.05 else 'Không phân phối chuẩn'}")
# Tạo Q-Q plot
stats.probplot(income, dist="norm", plot=axes[0, 1])
axes[0, 1].set_title('Q-Q Plot')
axes[0, 1].grid(True, alpha=0.3)
# Tạo P-P plot
sorted_data = np.sort(income)
p_theoretical = np.arange(1, len(sorted_data) + 1) / len(sorted_data)
p_observed = stats.norm.cdf(sorted_data, mu, sigma)
axes[1, 0].plot(p_theoretical, p_observed, 'bo', markersize=3)
axes[1, 0].plot([0, 1], [0, 1], 'r-', linewidth=2)
axes[1, 0].set_title('P-P Plot')
axes[1, 0].set_xlabel('Xác suất lý thuyết')
axes[1, 0].set_ylabel('Xác suất quan sát')
axes[1, 0].grid(True, alpha=0.3)
# Boxplot để phát hiện outliers
axes[1, 1].boxplot(income, vert=True)
axes[1, 1].set_title('Boxplot để phát hiện outliers')
axes[1, 1].set_ylabel('Thu nhập')
axes[1, 1].grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
# Ví dụ biến đổi dữ liệu nếu không có phân phối chuẩn
print(f"\nBIẾN ĐỔI DỮ LIỆU")
print("="*60)
# Chỉ lấy giá trị dương cho các phép biến đổi
income_positive = income[income > 0]
# Các phương pháp biến đổi
transformations = {
'Gốc': income_positive,
'Log': np.log(income_positive),
'Sqrt': np.sqrt(income_positive),
'Reciprocal': 1/income_positive,
'Square': income_positive**2
}
# Hàm kiểm tra phân phối chuẩn
def check_normality(data, name):
print(f"\n{name}:")
print("-" * 30)
# Thống kê mô tả
skew = stats.skew(data)
kurt = stats.kurtosis(data)
print(f"Skewness: {skew:.4f}")
print(f"Kurtosis: {kurt:.4f}")
# Kiểm định
if len(data) <= 5000: shapiro_stat, shapiro_p = stats.shapiro(data) print(f"Shapiro-Wilk p-value: {shapiro_p:.4f}") shapiro_result = "Chuẩn" if shapiro_p > 0.05 else "Không chuẩn"
print(f"Shapiro-Wilk: {shapiro_result}")
jb_stat, jb_p = jarque_bera(data)
print(f"Jarque-Bera p-value: {jb_p:.4f}")
jb_result = "Chuẩn" if jb_p > 0.05 else "Không chuẩn"
print(f"Jarque-Bera: {jb_result}")
return {
'name': name,
'skewness': skew,
'kurtosis': kurt,
'shapiro_p': shapiro_p if len(data) <= 5000 else np.nan,
'jb_p': jb_p
}
# Kiểm tra tất cả các biến đổi
results = []
for name, data in transformations.items():
result = check_normality(data, name)
results.append(result)
# Tạo bảng tóm tắt kết quả
results_df = pd.DataFrame(results)
print(f"\nBẢNG TÓM TẮT KẾT QUẢ:")
print("="*80)
print(results_df.to_string(index=False, float_format='%.4f'))
# Tạo biểu đồ so sánh các phương pháp biến đổi
fig, axes = plt.subplots(2, 3, figsize=(18, 12))
axes = axes.flatten()
for i, (name, data) in enumerate(transformations.items()):
if i < len(axes):
axes[i].hist(data, bins=30, density=True, alpha=0.7, color='lightblue', edgecolor='black')
# Thêm đường cong chuẩn
mu_trans, sigma_trans = np.mean(data), np.std(data)
x_trans = np.linspace(np.min(data), np.max(data), 100)
axes[i].plot(x_trans, stats.norm.pdf(x_trans, mu_trans, sigma_trans),
'r-', linewidth=2, label='Đường cong chuẩn')
axes[i].set_title(f'{name} (Skew: {stats.skew(data):.3f})')
axes[i].set_xlabel('Giá trị')
axes[i].set_ylabel('Mật độ')
axes[i].legend()
axes[i].grid(True, alpha=0.3)
# Ẩn subplot thừa
if len(transformations) < len(axes):
axes[-1].set_visible(False)
plt.tight_layout()
plt.show()
# Tìm phương pháp biến đổi tốt nhất
best_transformation = None
best_score = float('inf')
for result in results:
if not np.isnan(result['shapiro_p']):
# Điểm số dựa trên kết hợp của các tiêu chí
score = abs(result['skewness']) + abs(result['kurtosis']) - result['shapiro_p']
if score < best_score:
best_score = score
best_transformation = result['name']
if best_transformation:
print(f"\nPHƯƠNG PHÁP BIẾN ĐỔI TỐT NHẤT: {best_transformation}")
print("="*60)
# Hiển thị so sánh trước và sau biến đổi
original_data = income_positive
transformed_data = transformations[best_transformation]
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Histogram gốc
axes[0, 0].hist(original_data, bins=30, density=True, alpha=0.7, color='lightcoral')
axes[0, 0].set_title('Dữ liệu gốc')
axes[0, 0].set_xlabel('Thu nhập')
axes[0, 0].set_ylabel('Mật độ')
# Q-Q plot gốc
stats.probplot(original_data, dist="norm", plot=axes[0, 1])
axes[0, 1].set_title('Q-Q Plot - Dữ liệu gốc')
# Histogram sau biến đổi
axes[1, 0].hist(transformed_data, bins=30, density=True, alpha=0.7, color='lightgreen')
mu_best, sigma_best = np.mean(transformed_data), np.std(transformed_data)
x_best = np.linspace(np.min(transformed_data), np.max(transformed_data), 100)
axes[1, 0].plot(x_best, stats.norm.pdf(x_best, mu_best, sigma_best),
'r-', linewidth=2, label='Đường cong chuẩn')
axes[1, 0].set_title(f'Sau biến đổi {best_transformation}')
axes[1, 0].set_xlabel('Giá trị biến đổi')
axes[1, 0].set_ylabel('Mật độ')
axes[1, 0].legend()
# Q-Q plot sau biến đổi
stats.probplot(transformed_data, dist="norm", plot=axes[1, 1])
axes[1, 1].set_title(f'Q-Q Plot - Sau biến đổi {best_transformation}')
plt.tight_layout()
plt.show()
print(f"\nKẾT LUẬN:")
print("="*60)
print("1. Luôn kiểm tra phân phối chuẩn trước khi áp dụng kiểm định tham số")
print("2. Kết hợp nhiều phương pháp để có đánh giá toàn diện")
print("3. Xem xét biến đổi dữ liệu nếu cần thiết")
print("4. Với mẫu lớn, tập trung vào phân tích đồ thị hơn là kiểm định thống kê")
print("5. Nhớ rằng phân phối chuẩn là giả định lý tưởng, không phải yêu cầu tuyệt đối")
Tài liệu tham khảo
Để nắm vững hơn về giả định phân phối chuẩn trong thực hành kinh tế lượng, các bạn có thể tham khảo:
- IBM SPSS Statistics Documentation – Explore and Descriptive Statistics Procedures
- Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics (5th ed.). Sage Publications
- Gujarati, D. N., Porter, D. C., & Gunasekar, S. (2017). Basic Econometrics (5th ed.). McGraw-Hill Education
- Wooldridge, J. M. (2020). Introductory Econometrics: A Modern Approach (7th ed.). Cengage Learning
- Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2019). Multivariate Data Analysis (8th ed.). Cengage Learning
- Tabachnick, B. G., & Fidell, L. S. (2019). Using Multivariate Statistics (7th ed.). Pearson
- Razali, N. M., & Wah, Y. B. (2011). Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. Journal of Statistical Modeling and Analytics, 2(1), 21-33
- Thode, H. C. (2002). Testing for Normality. Marcel Dekker
Xem thêm các bài viết liên quan
Các chủ đề bổ sung giúp hiểu rõ hơn về giả định trong phân tích thống kê: