Lựa chọn trọng số: pweight hay fweight

Vấn đề về lựa chọn trọng số
Một trong những sai lầm phổ biến nhất xảy ra khi phân tích dữ liệu từ cuộc điều tra mẫu là lựa chọn trọng số của mẫu không phù hợp. Có 4 loại trọng số mẫu thường được sử dụng trong phân tích dữ liệu điều tra là:
- Trọng số xác suất: pweight (pw)
- Trọng số tần suất: fweight (fw)
- Trọng số phân tích: aweight (aw)
- Trọng số ảnh hưởng: iweight (iw)
Trong 4 loại trọng số trên, trọng số xác suất (chọn mẫu) và trọng số tần suất là 2 trọng số được sử dụng phổ biến nhất. Bài viết này sẽ lần lượt trình bày 4 loại trọng số trên.
1.Trọng số xác suất
Stata có một trọng số đặc biệt, pweight, để xác định các trọng số xác suất (Probability weights). Trọng số xác suất đôi khi còn gọi là trọng số lấy mẫu (sampling weights). Trọng số lấy mẫu cho biết một quan sát trong mẫu sẽ đại diện cho bao nhiêu quan sát trong tổng thể mà nó đại diện. Trọng số lấy mẫu được sử dụng phổ biến trong tính toán các ước lượng như tỷ lệ, trung bình và phân tích hồi quy.
Phương pháp hồi quy với phương sai chuẩn mạnh (robust variance) sẽ tự động sử dụng các trọng số xác suất để điều chỉnh các đặc điểm dữ liệu nhằm làm cho các kết quả ước lượng của phương sai, sai số chuẩn và khoảng tin cậy được chính xác.
Sử dụng bộ số liệu pweight.dta để minh họa kết quả hồi quy trong các trường hợp không có và có sử dụng trọng số xác suất (trường hợp không có tùy chọn robust và có tùy chọn robust). Bộ số liệu gồm 4029 quan sát từ cuộc khảo sát năm 1999 của phụ nữ Tanzania. Ở đây chúng ta ước đoán xác suất có 0 – 2 con (twokids) theo các biến giải thích là tuổi (age) và mức học vấn của người phụ nữ (educat).
Sử dụng hồi quy logit lần lượt cho các trường hợp trên như sau:
- Mô hình 1: logit twokids age educat
- Mô hình 2: logit twokids age educat [pweight=sampwt]
- Mô hình 3: logit twokids age educat [pweight=sampwt], cluster(earea)
Kết quả hồi quy logit của 3 mô hình trên được tổng hợp ở bảng sau:
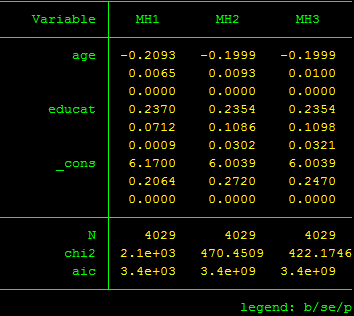
Kết quả cho thấy các mô hình đều có hiệu quả giải thích và hệ số ước lượng của cả 3 mô hình đều có ý nghĩa thống kê ở mức 5%. Tuy nhiên, giá trị hệ số ước lượng (trị tuyệt đối) của 2 biến giải thích ở mô hình 1 đều cao hơn đôi chút so với mô hình 2 và mô hình 3. Với giá trị cao hơn này sẽ dẫn đến khả năng một phụ nữ Tanzania sẽ sinh từ 0 – 2 con cao hơn so với 2 mô hình còn lại. Điều này chưa thực sự phù hợp với tổng thể, bởi chúng ta chỉ xét trên 4029 quan sát trong mẫu, mà chưa xét đến tính đại diện của mỗi quan sát đối với tổng thể.
Kết quả của mô hình 2 và mô hình 3 là tương đối giống nhau cả về giá trị hệ số lẫn sai số chuẩn của hệ số so với mô hình 1. Điều này có thể được lý giải như sau: mặc dù mô hình 2 không sử dụng sai số chuẩn mạnh để xét đến phần phương sai thay đổi như mô hình 3, nhưng mô hình 2 đã sử dụng trọng số – như là một cách điều chỉnh dữ liệu để hạn chế sự phân tán dữ liệu.
2.Trọng số tần suất
Trọng số tần suất (Frequency Weights), trong STATA được thể hiện bằng lệnh fweight, cho biết số lần xuất hiện của mỗi đối tượng trong mẫu dữ liệu. Nó được sử dụng khi dữ liệu của bạn được thu gọn (collapsed) và cùng với một biến đếm mới cho biết số lần xuất hiện của mỗi quan sát. Chẳng hạn, chúng ta có dữ liệu của các biến y x1 x2 như sau:
| x1 | x2 | y |
| 16 | 3 | 1 |
| 16 | 3 | 1 |
| 19 | 2 | 0 |
| 19 | 2 | 0 |
| 19 | 2 | 0 |
Giả sử chúng ta muốn hồi quy mô hình sau: logit y x1 x2 thì chúng ta phải thu gọn (collapsed) dữ liệu gốc trên thành dạng bên dưới
| x1 | x2 | y | count |
| 16 | 3 | 1 | 2 |
| 19 | 2 | 0 | 3 |
và sau đó thực hiện hồi quy logit mô hình với trọng số tần suất fweight như sau:
logit y x1 x2 [fweight=count]
Tuy nhiên trong trường hợp với cở mẫu rất nhỏ, thì phương pháp hồi quy logit không thể được thực hiện (vì ước lượng ML đòi hỏi phải có cở mẫu lớn). Trong trường hợp này, chúng ta phải sử dụng phương pháp hồi quy logit chính xác (Exact logit) như sau:
exlogistic y x1 [fweight=count]

Nếu chúng ta không sử dụng trọng số [fweight=count] thì kết quả ước lượng sẽ bị chệch bởi phương sai, sai số chuẩn được ước lượng sẽ bị lệch.
Kết quả ước lượng với câu lệnh exlogistic cùng với trọng số tần suất cho kết quả trung vị không chệch (MUE: Median Unbiased Estimates). Điều này cho thấy khi x1 tăng 1 đơn vị thì odds của biến y giảm 0.537 hay 53.7%.