Hệ số tương quan hạng Spearman
Thực hành Phân tích tương quan hạng Spearman với SPSS

Tóm tắt: Tương quan hạng Spearman là một phương pháp thống kê phi tham số được sử dụng để đánh giá mối quan hệ giữa hai biến khi dữ liệu không thỏa mãn giả định phân phối chuẩn. Phương pháp này đặc biệt hữu ích trong thực hành kinh tế lượng khi phân tích dữ liệu có tính chất thứ tự hoặc không tuân theo phân phối chuẩn. Bài viết hướng dẫn chi tiết cách thực hiện tương quan hạng Spearman trên SPSS với ví dụ thực tế từ dữ liệu bán hàng.
Giới thiệu
Nội dung chính
Trong thực hành kinh tế lượng, việc phân tích mối quan hệ giữa các biến số là một nhiệm vụ cơ bản và quan trọng. Tuy nhiên, không phải lúc nào dữ liệu cũng thỏa mãn các giả định cần thiết để sử dụng tương quan Pearson. Đặc biệt trong bối cảnh kinh tế Việt Nam, dữ liệu thu thập từ các doanh nghiệp nhỏ và vừa thường có phân phối không chuẩn hoặc chứa các giá trị ngoại lai.
Tương quan hạng Spearman ra đời như một giải pháp thay thế hiệu quả cho tương quan Pearson trong những trường hợp dữ liệu vi phạm giả định phân phối chuẩn. Phương pháp này được đặt tên theo Charles Spearman, nhà thống kê người Anh, và được sử dụng rộng rãi trong nghiên cứu kinh tế và xã hội.Ví dụ, khi phân tích mối quan hệ giữa thu nhập hộ gia đình và chi tiêu tiêu dùng tại các tỉnh thành Việt Nam, dữ liệu thu nhập thường có phân phối lệch phải do sự chênh lệch lớn giữa các nhóm thu nhập. Trong trường hợp này, tương quan hạng Spearman sẽ cho kết quả tin cậy hơn so với tương quan Pearson.
Giả định của tương quan hạng Spearman
Để thực hiện tương quan hạng Spearman một cách chính xác, dữ liệu cần thỏa mãn các giả định sau:
- Loại thang đo: Biến kiểm định có thể là dạng thứ tự (ordinal), tỉ lệ (ratio), khoảng (interval) và có phân phối bất kì. Tham khảo bài viết các loại thang đo trong phân tích dữ liệu.
- Tính đơn điệu: Các biến phải thỏa mãn tính chất đơn điệu (monotonic). Đây là giả định quan trọng nhất của tương quan hạng Spearman.
- Quan sát độc lập: Các quan sát phải độc lập với nhau, không có mối liên hệ nào giữa các quan sát.
- Dữ liệu cặp: Mỗi quan sát phải có cặp giá trị cho cả hai biến cần phân tích.
Giả thuyết H₀ cho rằng hệ số tương quan Spearman, ρ (rho), bằng 0. Hệ số ρ bằng 0 nghĩa là các hạng của một biến không thay đổi theo sự tăng/giảm các hạng của biến còn lại.
Xem thêm: Kiểm định phi tham số
Tính đơn điệu trong tương quan hạng Spearman
Tính đơn điệu giữa hai biến được thể hiện khi giá trị của một biến tăng thì cũng làm tăng giá trị của biến còn lại hoặc khi tăng giá trị của một biến thì làm giảm giá trị của biến còn lại. Tính đơn điệu của hai biến có thể minh họa qua hình bên dưới:
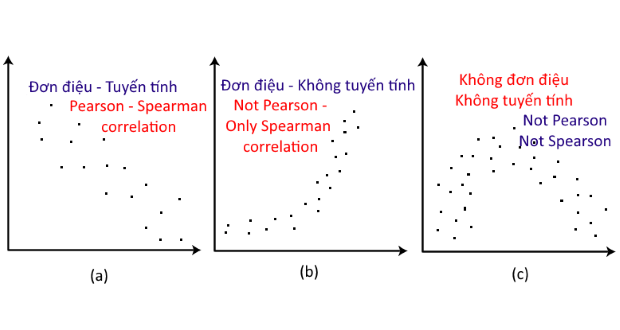
Tính đơn điệu ít bị hạn chế hơn mối quan hệ tuyến tính (linear relationship). Ở hình (b), không tồn tại mối quan hệ tuyến tính nhưng tồn tại tính đơn điệu giữa hai biến. Trường hợp này, bạn không thể sử dụng tương quan Pearson nhưng vẫn có thể sử dụng tương quan hạng Spearman.
Công thức tính toán
Tương quan hạng Spearman (ρ) có cách tính tương tự như hệ số tương quan Pearson (r), ngoại trừ bạn thực hiện trực tiếp trên các hạng (chứ không phải các dữ liệu đo lường). Các bước tính toán cụ thể như sau:
Bước 1: Xếp hạng dữ liệu
Xếp hạng các biến theo thứ tự giảm dần. Để chuyển một biến đo lường thành biến hạng, gán giá trị cao nhất là 1, kế tiếp là 2 và tương tự vậy. Sử dụng hạng trung bình cho các quan sát có giá trị đo lường bằng nhau.
Bước 2: Tính chênh lệch hạng
Tính toán sự chênh lệch hạng của từng cặp biến \(d_i\) theo công thức:
$$d_i = R(x_i) – R(y_i)$$
Trong đó: \(R(x_i)\) và \(R(y_i)\) là hạng của quan sát thứ i trong biến x và y
Bước 3: Tính hệ số tương quan hạng
Tính hệ số tương quan hạng ρ theo hai trường hợp:
- Trường hợp không có hạng bằng nhau:
$$\rho = 1 – \frac{6\sum_{i=1}^n d_i^2}{n(n^2-1)}$$
- Trường hợp có hạng bằng nhau:
$$\rho = \frac{\sum_{i=1}^n (x_i – \bar{x})(y_i – \bar{y})}{\sqrt{\sum_{i=1}^n (x_i – \bar{x})^2 \sum_{i=1}^n (y_i – \bar{y})^2}}$$
Bước 4: Kiểm định thống kê
Tính và so sánh giá trị thống kê t:
- Đối với số quan sát trên 10, thay r bằng ρ trong công thức tính giá trị thống kê t như sau:
$$t_s = \frac{\rho\sqrt{n-2}}{\sqrt{1-\rho^2}}$$
- Nếu số quan sát từ 10 trở xuống thì tính toán t và giá trị p (p-value) từ phân phối chuẩn t sẽ không còn chính xác. Khi đó, có thể sử dụng cách tra bảng (thống kê t) ứng với số quan sát để có được những giá trị này.
Ví dụ thực tế từ kinh tế Việt Nam
Sử dụng số liệu về chiến lược bán hàng được thu thập từ 25 cửa hàng điện thoại di động tại TP.HCM. Dữ liệu bao gồm doanh số bán hàng ứng với ba chiến lược: bán bình thường, bán giảm giá và bán kèm quà tặng.
Tải dữ liệu thực hành SpearmanĐặc điểm của dữ liệu:
- Dữ liệu của các biến có ít nhất một biến (none, discount, gift) không có phân phối chuẩn theo bất kì tiêu chí kiểm định phân phối chuẩn nào. Xem thêm Kiểm định Friedman và Kiểm tra phân phối chuẩn.
- Một trong hai biến thực hành không có phân phối chuẩn, về nguyên tắc, tương quan Pearson là không phù hợp sử dụng. Tuy nhiên, trong phần thực hành minh họa này, chúng ta sẽ so sánh cả hai cách để có sự kiểm chứng.
Hướng dẫn thực hành chi tiết trên SPSS
Trên SPSS, tương quan hạng Spearman được thực hiện theo các bước sau:
Vào Analyze → Correlate → Bivariate…

Bước 2: Thiết lập biến phân tích
Cửa sổ Bivariate Correlations mở ra. Thực hiện các thao tác sau:
- Đưa 2 biến none và biến discount vào ô Variables
- Thiết lập nút Options… như hình bên dưới

Bấm Continue và OK để tiến hành thực hiện phân tích.
Bước 3: Giải thích kết quả
Kết quả phân tích tương quan hạng Spearman gồm hai phần chính:
Thống kê mô tả
Bảng Descriptive Statistics cung cấp thông tin thống kê mô tả về giá trị trung bình, độ lệch chuẩn và số quan sát của mỗi biến. Theo kết quả, số lượng sản phẩm smartphone trung bình được bán ở các cửa hàng trong trường hợp có giảm giá cao hơn so với bán bình thường.
Bảng tương quan
Bảng Correlations cho biết kết quả tính toán hệ số tương quan Pearson và tương quan hạng Spearman:

Giải thích kết quả phân tích
Kết quả cho thấy một số điểm quan trọng:
- Độ tương quan: Không có sự chênh lệch lớn cả về độ lớn lẫn mức ý nghĩa giữa hệ số tương quan Pearson và hệ số tương quan hạng Spearman
- Mức độ quan hệ: Cả hai đều cho thấy mức tương quan dương tương đối (0.55 – 0.58) giữa doanh số bán hàng thông thường và doanh số bán hàng khi có giảm giá
- Mức ý nghĩa: Kết quả có ý nghĩa thống kê ở mức 1% (p < 0.01)
Điều này cho thấy rằng các cửa hàng có doanh số bán hàng cao trong điều kiện bình thường thường cũng có xu hướng đạt doanh số cao khi áp dụng chính sách giảm giá. Mối quan hệ này có thể phản ánh khả năng quản lý và vị trí kinh doanh của các cửa hàng.
Liên hệ với các phương pháp khác
Phân tích tương quan có nhiều điểm tương đồng với hồi quy tuyến tính giản đơn, tuy nhiên, chúng ta không thể đồng nhất việc thực hiện giữa hai phương pháp.
Tham khảo bài Tương quan và hồi quy tuyến tính giản đơn để có cách nhìn rõ ràng hơn về sự khác biệt giữa hai phương pháp này.
Nhiều người sử dụng tương quan hạng Spearman như một phương pháp thay thế cho tương quan Pearson khi dữ liệu không thỏa mãn điều kiện phân phối chuẩn. Tương quan Pearson giả định rằng dữ liệu phải có phân phối chuẩn, trong khi tương quan hạng Spearman không đòi hỏi giả định này. Tuy nhiên, nhiều nghiên cứu thực nghiệm cho thấy tương quan Pearson ít nhạy cảm với việc vi phạm giả định phân phối chuẩn. Điều này có nghĩa là ngay cả khi dữ liệu không hoàn toàn tuân theo phân phối chuẩn, tương quan Pearson vẫn có thể cho kết quả đáng tin cậy. Vì vậy, việc lựa chọn phương pháp nào phụ thuộc vào mức độ vi phạm giả định và tính chất của dữ liệu.
Lưu ý quan trọng khi sử dụng
- Tương quan hạng Spearman chỉ đo lường mức độ quan hệ, không chỉ ra mối quan hệ nhân quả
- Không vẽ đường hồi quy khi sử dụng tương quan hạng Spearman
- Phương pháp này nhạy cảm với các hạng bằng nhau (tied ranks)
- Kết quả chỉ có ý nghĩa khi dữ liệu thỏa mãn giả định tính đơn điệu
Tổng kết
Tương quan hạng Spearman là một công cụ mạnh mẽ trong thực hành kinh tế lượng, đặc biệt hữu ích khi phân tích dữ liệu không tuân theo phân phối chuẩn. Phương pháp này cung cấp một cách tiếp cận linh hoạt để đánh giá mối quan hệ giữa các biến số trong nghiên cứu kinh tế và xã hội.
Trong ví dụ thực hành với dữ liệu bán hàng, chúng ta thấy rằng tương quan hạng Spearman cho kết quả tương tự như tương quan Pearson, điều này phần nào khẳng định tính robust của phương pháp truyền thống ngay cả khi dữ liệu vi phạm giả định phân phối chuẩn.
Việc thành thạo cả hai phương pháp sẽ giúp nhà nghiên cứu có thêm lựa chọn phù hợp trong từng tình huống cụ thể, từ đó đưa ra kết luận chính xác và đáng tin cậy hơn trong phân tích dữ liệu.
Điểm quan trọng cần nhớ:
- Tương quan hạng Spearman là phương pháp phi tham số, không yêu cầu dữ liệu có phân phối chuẩn
- Phương pháp này đo lường mối quan hệ đơn điệu, không nhất thiết phải tuyến tính
- Sử dụng hạng thay vì giá trị gốc giúp giảm thiểu ảnh hưởng của các giá trị ngoại lai
- Kết quả cần được giải thích cẩn thận, tránh nhầm lẫn tương quan với nhân quả
- Trong nhiều trường hợp, tương quan Pearson vẫn cho kết quả tin cậy ngay cả khi dữ liệu vi phạm giả định phân phối chuẩn
Phụ lục
SPSS Syntax
SPSS Syntax (.sps)
* Phân tích tương quan hạng Spearman
* Tải dữ liệu
GET FILE='/data/friedman.sav'.
* Kiểm tra dữ liệu
DESCRIPTIVES VARIABLES=none discount gift
/STATISTICS=MEAN STDDEV MIN MAX.
* Thực hiện tương quan Pearson và Spearman
CORRELATIONS
/VARIABLES=none discount gift
/PRINT=TWOTAIL NOSIG
/STATISTICS DESCRIPTIVES
/MISSING=PAIRWISE.
NONPAR CORR
/VARIABLES=none discount gift
/PRINT=SPEARMAN TWOTAIL NOSIG
/MISSING=PAIRWISE.
* Kiểm tra phân phối chuẩn
EXAMINE VARIABLES=none discount gift
/PLOT BOXPLOT STEMLEAF NPPLOT
/COMPARE GROUPS
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
Stata Code
Stata Code (.do)
* Phân tích tương quan hạng Spearman trong Stata
* Tải dữ liệu
use "/data/friedman.dta", clear
* Kiểm tra dữ liệu
summarize none discount gift
* Thực hiện tương quan Pearson
corr none discount gift
* Thực hiện tương quan Spearman
spearman none discount gift
* Kiểm tra phân phối chuẩn
swilk none discount gift
* Vẽ biểu đồ scatter để kiểm tra tính đơn điệu
scatter discount none
scatter gift none
* Tạo matrix tương quan với kiểm định
pwcorr none discount gift, sig
* Tương quan Spearman với kiểm định
spearman none discount gift, stats(rho obs p)
* Xuất kết quả
matrix list r(C)
matrix list r(P)
R Code
R Code (.R)
# Phân tích tương quan hạng Spearman trong R
# Tải các thư viện cần thiết
library(foreign)
library(psych)
library(corrplot)
# Tải dữ liệu
data <- read.spss("/data/friedman.sav", to.data.frame=TRUE)
# Kiểm tra dữ liệu
summary(data[c("none", "discount", "gift")])
# Thực hiện tương quan Pearson
cor_pearson <- cor(data[c("none", "discount", "gift")],
use="complete.obs", method="pearson")
print(cor_pearson)
# Thực hiện tương quan Spearman
cor_spearman <- cor(data[c("none", "discount", "gift")],
use="complete.obs", method="spearman")
print(cor_spearman)
# Kiểm định tương quan với p-value
cor.test(data$none, data$discount, method="pearson")
cor.test(data$none, data$discount, method="spearman")
# Kiểm tra phân phối chuẩn
shapiro.test(data$none)
shapiro.test(data$discount)
shapiro.test(data$gift)
# Vẽ biểu đồ
plot(data$none, data$discount, main="Scatter Plot: None vs Discount")
plot(data$none, data$gift, main="Scatter Plot: None vs Gift")
# Ma trận tương quan với visualization
corrplot(cor_spearman, method="color", type="upper",
tl.cex=0.8, tl.col="black")
# Tương quan với thống kê đầy đủ
corr.test(data[c("none", "discount", "gift")], method="spearman")
Python Code
Python Code (.py)
# Phân tích tương quan hạng Spearman trong Python
import pandas as pd
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import pearsonr, spearmanr
# Tải dữ liệu
data = pd.read_spss('/data/friedman.sav')
# Kiểm tra dữ liệu
print(data[['none', 'discount', 'gift']].describe())
# Thực hiện tương quan Pearson
corr_pearson = data[['none', 'discount', 'gift']].corr(method='pearson')
print("Tương quan Pearson:")
print(corr_pearson)
# Thực hiện tương quan Spearman
corr_spearman = data[['none', 'discount', 'gift']].corr(method='spearman')
print("\nTương quan Spearman:")
print(corr_spearman)
# Kiểm định tương quan cụ thể
pearson_coef, pearson_p = pearsonr(data['none'], data['discount'])
spearman_coef, spearman_p = spearmanr(data['none'], data['discount'])
print(f"\nPearson correlation: {pearson_coef:.4f}, p-value: {pearson_p:.4f}")
print(f"Spearman correlation: {spearman_coef:.4f}, p-value: {spearman_p:.4f}")
# Kiểm tra phân phối chuẩn
shapiro_none = stats.shapiro(data['none'])
shapiro_discount = stats.shapiro(data['discount'])
shapiro_gift = stats.shapiro(data['gift'])
print(f"\nShapiro-Wilk test for 'none': {shapiro_none.pvalue:.4f}")
print(f"Shapiro-Wilk test for 'discount': {shapiro_discount.pvalue:.4f}")
print(f"Shapiro-Wilk test for 'gift': {shapiro_gift.pvalue:.4f}")
# Vẽ biểu đồ
plt.figure(figsize=(12, 4))
plt.subplot(1, 3, 1)
plt.scatter(data['none'], data['discount'])
plt.xlabel('None')
plt.ylabel('Discount')
plt.title('Scatter Plot: None vs Discount')
plt.subplot(1, 3, 2)
plt.scatter(data['none'], data['gift'])
plt.xlabel('None')
plt.ylabel('Gift')
plt.title('Scatter Plot: None vs Gift')
plt.subplot(1, 3, 3)
sns.heatmap(corr_spearman, annot=True, cmap='coolwarm', center=0)
plt.title('Spearman Correlation Matrix')
plt.tight_layout()
plt.show()
# Ma trận tương quan chi tiết
def correlation_matrix_with_pvalue(df):
columns = df.columns
corr_matrix = np.zeros((len(columns), len(columns)))
p_matrix = np.zeros((len(columns), len(columns)))
for i, col1 in enumerate(columns):
for j, col2 in enumerate(columns):
if i == j:
corr_matrix[i, j] = 1.0
p_matrix[i, j] = 0.0
else:
corr, p_val = spearmanr(df[col1], df[col2])
corr_matrix[i, j] = corr
p_matrix[i, j] = p_val
return corr_matrix, p_matrix
corr_matrix, p_matrix = correlation_matrix_with_pvalue(data[['none', 'discount', 'gift']])
print("\nSpearman Correlation Matrix:")
print(corr_matrix)
print("\nP-value Matrix:")
print(p_matrix)
Tài liệu tham khảo
1. Edgell, S.E., and S.M. Noon. 1984. Effect of violation of normality on the t-test of the correlation coefficient. Psychological Bulletin. 95: 576-583.
2. Spearman, C. 1904. The proof and measurement of association between two things. The American Journal of Psychology. 15(1): 72-101.
3. Siegel, S., & Castellan, N. J. 1988. Nonparametric statistics for the behavioral sciences. McGraw-Hill.
4. Field, A. 2018. Discovering statistics using IBM SPSS statistics (5th ed.). SAGE Publications.
5. Howell, D. C. 2017. Statistical methods for psychology (8th ed.). Cengage Learning.