Hồi quy logit giản đơn
Hồi quy logit giản đơn trong thực hành kinh tế lượng với SPSS

Tóm tắt: Hồi quy logit giản đơn là phương pháp thống kê quan trọng trong thực hành kinh tế lượng để phân tích mối quan hệ giữa biến phụ thuộc nhị phân và biến độc lập. Bài viết hướng dẫn chi tiết cách thực hiện hồi quy logit giản đơn bằng SPSS, từ thiết lập dữ liệu đến diễn giải kết quả, kèm theo các ví dụ thực tế trong kinh tế Việt Nam như dự báo xác suất khởi nghiệp, quyết định đầu tư, và phân tích hành vi tiêu dùng.
Giới thiệu về hồi quy logit trong kinh tế lượng
Nội dung chính
- Giới thiệu về hồi quy logit trong kinh tế lượng
- Giả thiết của hồi quy logit giản đơn
- Cơ sở lý thuyết và công thức toán học
- Ví dụ thực tế từ kinh tế Việt Nam
- Hướng dẫn thực hành chi tiết với SPSS
- Giải thích kết quả hồi quy logit
- Dự báo xác suất từ mô hình
- Lưu ý quan trọng trong thực hành
- Kết luận
- Phụ lục – Code tương đương cho các phần mềm khác
- Tài liệu tham khảo
Trong thực hành kinh tế lượng, chúng ta thường gặp các tình huống mà biến phụ thuộc nhị phân đóng vai trò then chốt. Khác với phân tích hồi quy tuyến tính truyền thống xử lý biến phụ thuộc liên tục, hồi quy logit giản đơn được thiết kế đặc biệt cho các biến kết quả có dạng có/không.
Trong bối cảnh kinh tế Việt Nam, hồi quy logit giản đơn có nhiều ứng dụng thực tế:
- Dự báo xác suất một doanh nghiệp nhỏ thành công dựa trên vốn ban đầu
- Phân tích yếu tố ảnh hưởng đến quyết định mua nhà của các hộ gia đình
- Nghiên cứu tác động của thu nhập đến khả năng tiếp cận dịch vụ y tế
- Đánh giá hiệu quả chính sách hỗ trợ nông nghiệp
Ví dụ minh họa: Giả sử chúng ta nghiên cứu tác động của chi tiêu quảng cáo đến quyết định mua sản phẩm của người tiêu dùng Việt Nam. Biến phụ thuộc là quyết định mua (1: có mua, 0: không mua), biến độc lập là mức chi tiêu quảng cáo. Hồi quy logit giúp chúng ta không chỉ xác định mối quan hệ này mà còn dự báo xác suất mua hàng ở các mức chi tiêu quảng cáo khác nhau.
Giả thiết của hồi quy logit giản đơn
Để thực hiện hồi quy logit giản đơn một cách chính xác, chúng ta cần đảm bảo bốn giả thiết cơ bản:
- Biến phụ thuộc nhị phân: Biến kết quả phải có dạng nhị phân (0 hoặc 1). Trong thực hành kinh tế lượng, điều này thường được mã hóa từ các biến định tính như thành công/thất bại, có/không có.
- Biến độc lập đa dạng: Có thể sử dụng biến liên tục (thu nhập, tuổi) hoặc biến phân loại (giới tính, trình độ học vấn).
- Tính độc lập của quan sát: Mỗi quan sát phải độc lập và biến phụ thuộc phải có tính loại trừ lẫn nhau.
- Quan hệ tuyến tính với logit: Tồn tại mối quan hệ tuyến tính giữa biến độc lập và logarit của odds của biến phụ thuộc.
Cơ sở lý thuyết và công thức toán học
Hồi quy logit giản đơn dựa trên việc biến đổi xác suất thành hàm logit để tạo ra mối quan hệ tuyến tính:
Các khái niệm cơ bản
- Xác suất (p): Khả năng xảy ra của biến cố, tính bằng x/n
- Odds: Tỷ lệ khả năng xảy ra so với không xảy ra
- Logit: Logarit tự nhiên của odds
- Odds ratio: Tỷ số odds giữa hai nhóm
Công thức odds: \(odds(p|x) = \frac{p}{1 – p}\)
Hàm logit: \(logit(p) = \log \left(\frac{p}{1 – p}\right) = \log(odds)\)
Mô hình hồi quy logit: \(logit(p) = \alpha + \beta x\)
Trong đó, \(\alpha\) và \(\beta\) được ước lượng bằng phương pháp hợp lý cực đại (ML).
Odds ratio: \(OR = \frac{odds(p|x_0 + 1)}{odds(p|x_0)} = e^{\beta}\)
Công thức dự báo xác suất: \(\hat{p} = \frac{1}{1 + e^{-(\hat{\alpha} + \hat{\beta}x)}}\)
Ví dụ thực tế từ kinh tế Việt Nam
Để minh họa ứng dụng hồi quy logit giản đơn trong thực hành kinh tế lượng, chúng ta sử dụng ví dụ về quyết định khởi nghiệp của sinh viên mới tốt nghiệp tại Việt Nam.
Bối cảnh nghiên cứu: Phân tích tác động của điểm trung bình tích lũy (GPA) đến quyết định khởi nghiệp của sinh viên kinh tế.
Biến số:
- Biến phụ thuộc (y): Quyết định khởi nghiệp (1: có, 0: không)
- Biến độc lập (x): Điểm GPA (thang 4.0)
Giả thuyết nghiên cứu: Sinh viên có GPA cao có xu hướng khởi nghiệp nhiều hơn do tự tin vào năng lực.
Sử dụng file dữ liệu hồi quy logit với ba biến x1, x2 và x3. Trong đó, biến x1 là biến liên tục, x2 là biến nhị phân và biến x3 là biến phân loại ba mức.
Hướng dẫn thực hành chi tiết với SPSS
Quá trình thực hiện hồi quy logit giản đơn trong SPSS được thực hiện theo các bước sau:
Vào menu Analyze → Regression → Binary Logistic…
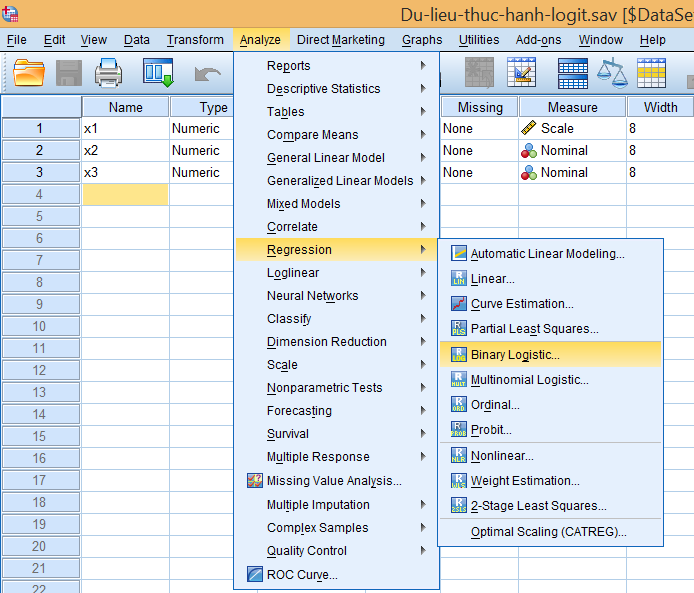
Bước 2: Thiết lập biến số
Cửa sổ Logistic Regression xuất hiện với các tùy chọn:
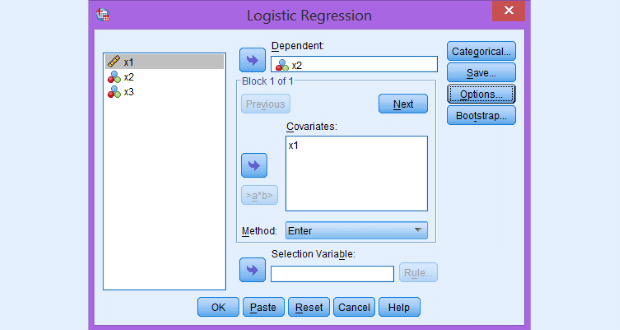
- Chọn biến phụ thuộc nhị phân vào ô Dependent
- Chọn biến độc lập vào ô Covariates
- Kiểm tra phương pháp nhập biến (Method: Enter)
Bước 3: Thiết lập các tùy chọn nâng cao
Nhấp nút Options… để cấu hình các tùy chọn quan trọng:
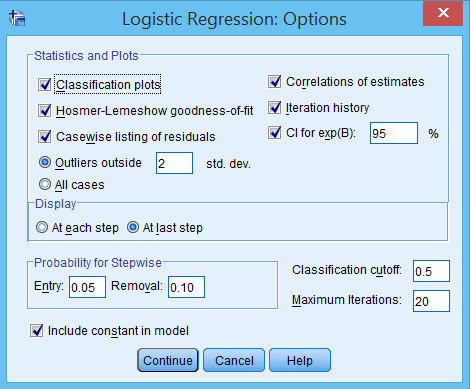
- Classification plots: Biểu đồ phân loại để đánh giá hiệu suất mô hình
- Hosmer-Lemeshow goodness-of-fit: Kiểm định độ phù hợp quan trọng
- Correlations of estimates: Ma trận tương quan giữa các ước lượng
- Iteration history: Lịch sử quá trình lặp của thuật toán
- CI for exp(B): Khoảng tin cậy cho odds ratio
Giải thích kết quả hồi quy logit
Kết quả SPSS cung cấp nhiều bảng thông tin quan trọng để đánh giá mô hình:
Phần 1: Mô tả dữ liệu
Bảng Case Processing Summary: Tổng quan về dữ liệu
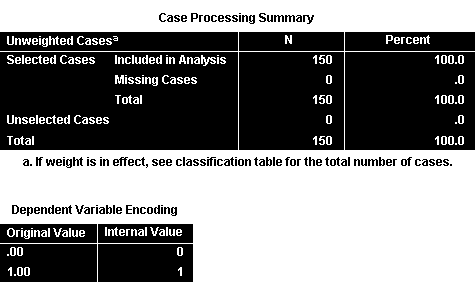
Bảng này hiển thị:
- Số quan sát được bao gồm trong phân tích
- Số quan sát bị loại trừ do thiếu dữ liệu
- Tổng số quan sát ban đầu
Bảng Dependent Variable Encoding: Mã hóa biến phụ thuộc
Bảng này cho thấy cách SPSS mã hóa biến phụ thuộc nhị phân. Trong trường hợp này, giá trị gốc và giá trị nội bộ giống nhau vì dữ liệu đã được mã hóa sẵn.
Phần 2: Mô hình cơ sở (Null Model)
Beginning Block: Phân tích mô hình chỉ có hằng số
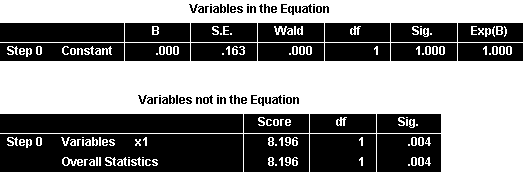
Mô hình null (chỉ có hằng số) được sử dụng làm cơ sở so sánh với mô hình hoàn chỉnh:
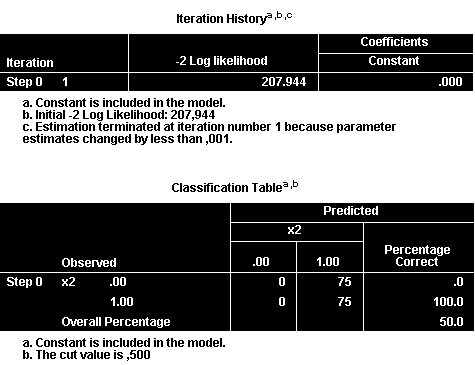
Classification Table: Bảng phân loại của mô hình null cho thấy khả năng dự báo chính xác là 50% (tương đương với dự báo ngẫu nhiên).
Phần 3: Mô hình hoàn chỉnh (Full Model)
Iteration History: Lịch sử quá trình lặp
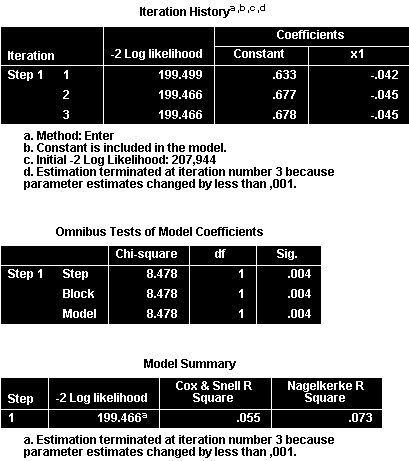
Quá trình lặp kết thúc ở bước 3 khi sự thay đổi các tham số < 0.001. Giá trị -2LL giảm từ 204.944 xuống 199.466, cho thấy mô hình cải thiện đáng kể.
Omnibus Tests of Model Coefficients: Kiểm định tổng thể mô hình
Với p-value = 0.04 < 0.05, mô hình hoàn chỉnh có ý nghĩa thống kê so với mô hình null.
Model Summary: Tóm tắt mô hình
- Cox & Snell R²: Phiên bản R² được điều chỉnh cho mô hình logit
- Nagelkerke R²: Phiên bản R² chuẩn hóa trong khoảng 0-1
- Các R² này chỉ dùng để so sánh các mô hình, không phải thước đo độ phù hợp tuyệt đối
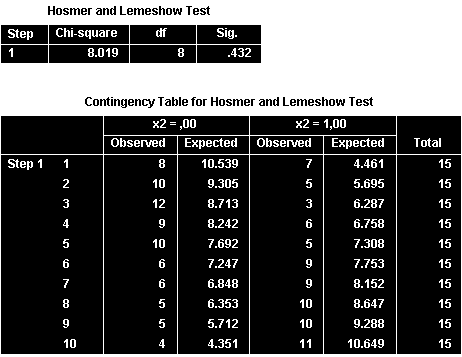
Hosmer and Lemeshow Test: Kiểm định độ phù hợp
Với χ² = 8.019, df = 8, p = 0.432 > 0.05, mô hình phù hợp tốt với dữ liệu quan sát.
Classification Table: Bảng phân loại mô hình hoàn chỉnh
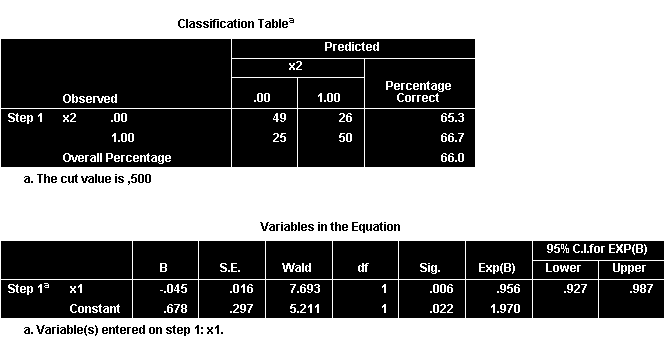
Mô hình dự báo chính xác 66% các quan sát, cải thiện 16% so với mô hình null.
Quy tắc đánh giá hiệu suất: Phần trăm dự báo chính xác phải ≥ (Phần trăm nhóm lớn nhất)² + 25%. Trong trường hợp này, với phân bố 50-50, ngưỡng tối thiểu là 50% + 25% = 75%. Mô hình với 66% chưa đạt ngưỡng lý tưởng.
Phần 4: Hệ số hồi quy và diễn giải
Bảng Variables in the Equation: Hệ số hồi quy chính
Kết quả quan trọng nhất của phân tích:
- Hệ số B = -0.045: Hệ số logit cho biến x1
- Kiểm định Wald: p-value = 0.006 < 0.01 (có ý nghĩa thống kê mức 1%)
- Exp(B) = 0.956: Odds ratio = tỷ số khả dĩ
Diễn giải kết quả:
- Hệ số β âm cho thấy mối quan hệ nghịch: khi x1 tăng, xác suất x2 = 1 giảm
- Odds ratio = 0.956 có nghĩa: khi x1 tăng 1 đơn vị, odds giảm 4.4%
- Công thức dự báo: \(\hat{p} = \frac{1}{1 + e^{-(0.678 – 0.045x_1)}}\)
Dự báo xác suất từ mô hình
Để minh họa khả năng dự báo của mô hình, chúng ta tính toán xác suất tại các giá trị khác nhau của x1:
| Giá trị x1 | Logit | Xác suất dự báo | % Thay đổi |
|---|---|---|---|
| -10 | -2.970 | 0.692 | – |
| -5 | -1.485 | 0.678 | -2.02% |
| 0 | 0 | 0.663 | -2.21% |
| 5 | 1.485 | 0.648 | -2.26% |
| 10 | 2.970 | 0.633 | -2.31% |
Lưu ý quan trọng trong thực hành
Các vấn đề thường gặp
- Không kiểm tra tính tuyến tính của mối quan hệ logit
- Bỏ qua kiểm định Hosmer-Lemeshow
- Diễn giải sai odds ratio
- Không kiểm tra các điểm dị biệt (outliers)
Đánh giá chất lượng mô hình
- Kiểm định Hosmer-Lemeshow có p-value > 0.05
- Khả năng dự báo > ngưỡng tối thiểu theo quy tắc 25%
- Các hệ số có ý nghĩa thống kê
- Biểu đồ residual không có pattern bất thường
Kết luận
Hồi quy logit giản đơn là công cụ mạnh mẽ trong thực hành kinh tế lượng để phân tích các biến phụ thuộc nhị phân. Thông qua ví dụ minh họa, chúng ta đã học cách:
- Thiết lập và thực hiện hồi quy logit trong SPSS
- Diễn giải các kết quả thống kê quan trọng
- Đánh giá độ phù hợp và chất lượng mô hình
- Dự báo xác suất từ mô hình ước lượng
Phương pháp này đặc biệt hữu ích trong nghiên cứu kinh tế Việt Nam, từ phân tích hành vi tiêu dùng đến đánh giá hiệu quả chính sách. Việc nắm vững hồi quy logit mở ra nhiều cơ hội nghiên cứu thực tiễn trong lĩnh vực kinh tế.
Điểm then chốt:
- Hồi quy logit giản đơn phù hợp với biến phụ thuộc nhị phân
- Sử dụng Maximum Likelihood để ước lượng tham số
- Odds ratio là thước đo tác động quan trọng nhất
- Kiểm định Hosmer-Lemeshow đánh giá độ phù hợp mô hình
- Khả năng dự báo phải vượt ngưỡng tối thiểu theo quy tắc 25%
Phụ lục – Code tương đương cho các phần mềm khác
Để hỗ trợ sinh viên làm quen với nhiều phần mềm thống kê khác nhau, dưới đây là code tương đương cho hồi quy logit giản đơn:
SPSS Syntax
SPSS Syntax (.sps)
* Hồi quy logit giản đơn trong SPSS
* Tác giả: Thực hành kinh tế lượng
* Mô tả: Phân tích mối quan hệ giữa biến nhị phân x2 và biến liên tục x1
* Mở file dữ liệu
GET FILE='/data/logit.sav'.
* Thực hiện hồi quy logit
LOGISTIC REGRESSION VARIABLES x2
/METHOD=ENTER x1
/CONTRAST (x1)=Indicator
/PRINT=GOODFIT ITER(1) CI(95)
/CRITERIA=PIN(0.05) POUT(0.10) ITERATE(20) CUT(0.5).
* Lưu giá trị dự báo
LOGISTIC REGRESSION VARIABLES x2
/METHOD=ENTER x1
/SAVE=PRED PGROUP RESID ZRESID.
* Thống kê mô tả kết quả
FREQUENCIES VARIABLES=PRE_1 PGR_1.
DESCRIPTIVES VARIABLES=ZRE_1.
Stata Code
Stata Code (.do)
* Hồi quy logit giản đơn trong Stata
* Tác giả: Thực hành kinh tế lượng
* Mô tả: Phân tích mối quan hệ giữa biến nhị phân x2 và biến liên tục x1
* Mở file dữ liệu
use "/data/logit.dta", clear
* Thống kê mô tả ban đầu
summarize x1 x2
tabulate x2
* Thực hiện hồi quy logit
logit x2 x1
* Hiển thị odds ratio
logit x2 x1, or
* Kiểm định Hosmer-Lemeshow
estat gof, group(10)
* Dự báo xác suất
predict phat, pr
* Đánh giá khả năng phân loại
estat classification
* Biểu đồ dự báo
scatter phat x1, jitter(5) || lfit phat x1
R Code
R Code (.R)
# Hồi quy logit giản đơn trong R
# Tác giả: Thực hành kinh tế lượng
# Mô tả: Phân tích mối quan hệ giữa biến nhị phân x2 và biến liên tục x1
# Tải các thư viện cần thiết
library(foreign) # Đọc file SPSS
library(ResourceSelection) # Kiểm định Hosmer-Lemeshow
library(pROC) # Đường cong ROC
library(ggplot2) # Vẽ biểu đồ
# Đọc dữ liệu
data <- read.spss("/data/logit.sav", to.data.frame = TRUE)
# Thống kê mô tả
summary(data)
table(data$x2)
# Thực hiện hồi quy logit
model <- glm(x2 ~ x1, data = data, family = binomial)
# Hiển thị kết quả
summary(model)
# Odds ratio và khoảng tin cậy
exp(coef(model))
exp(confint(model))
# Kiểm định Hosmer-Lemeshow
hoslem.test(data$x2, fitted(model))
# Dự báo xác suất
predicted_prob <- predict(model, type = "response")
# Đánh giá khả năng phân loại
predicted_class <- ifelse(predicted_prob > 0.5, 1, 0)
confusion_matrix <- table(data$x2, predicted_class)
accuracy <- sum(diag(confusion_matrix)) / sum(confusion_matrix)
print(paste("Accuracy:", round(accuracy, 3)))
# Vẽ biểu đồ dự báo
ggplot(data, aes(x = x1, y = x2)) +
geom_point(alpha = 0.6) +
geom_smooth(method = "glm", method.args = list(family = "binomial")) +
labs(title = "Hồi quy logit: Mối quan hệ giữa x1 và x2",
x = "Biến độc lập (x1)", y = "Xác suất (x2 = 1)")
Python Code
Python Code (.py)
# Hồi quy logit giản đơn trong Python
# Tác giả: Thực hành kinh tế lượng
# Mô tả: Phân tích mối quan hệ giữa biến nhị phân x2 và biến liên tục x1
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy import stats
import statsmodels.api as sm
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.linear_model import LogisticRegression
# Đọc dữ liệu
data = pd.read_spss('/data/logit.sav')
# Thống kê mô tả
print("Thống kê mô tả:")
print(data.describe())
print("\nBảng tần số x2:")
print(data['x2'].value_counts())
# Chuẩn bị dữ liệu cho mô hình
X = data['x1']
y = data['x2']
X_with_const = sm.add_constant(X) # Thêm hằng số
# Thực hiện hồi quy logit với statsmodels
model = sm.Logit(y, X_with_const)
result = model.fit()
# Hiển thị kết quả chi tiết
print("\nKết quả hồi quy logit:")
print(result.summary())
# Odds ratio
odds_ratio = np.exp(result.params)
print(f"\nOdds Ratio cho x1: {odds_ratio['x1']:.3f}")
# Dự báo xác suất
predicted_prob = result.predict(X_with_const)
# Đánh giá mô hình
predicted_class = (predicted_prob > 0.5).astype(int)
accuracy = np.mean(predicted_class == y)
print(f"\nĐộ chính xác: {accuracy:.3f}")
# Ma trận nhầm lẫn
conf_matrix = confusion_matrix(y, predicted_class)
print("\nMa trận nhầm lẫn:")
print(conf_matrix)
# Vẽ biểu đồ
plt.figure(figsize=(12, 5))
# Biểu đồ phân tán với đường hồi quy
plt.subplot(1, 2, 1)
plt.scatter(X, y, alpha=0.6)
plt.plot(X, predicted_prob, color='red', linewidth=2)
plt.xlabel('Biến độc lập (x1)')
plt.ylabel('Xác suất (x2 = 1)')
plt.title('Hồi quy logit: Mối quan hệ x1 và x2')
# Biểu đồ phân phối xác suất dự báo
plt.subplot(1, 2, 2)
plt.hist(predicted_prob, bins=20, alpha=0.7, edgecolor='black')
plt.xlabel('Xác suất dự báo')
plt.ylabel('Tần số')
plt.title('Phân phối xác suất dự báo')
plt.tight_layout()
plt.show()
# Kiểm định Hosmer-Lemeshow (tự thực hiện)
def hosmer_lemeshow_test(y_true, y_prob, n_bins=10):
"""Kiểm định Hosmer-Lemeshow tự thực hiện"""
# Chia dữ liệu thành các nhóm
df = pd.DataFrame({'y_true': y_true, 'y_prob': y_prob})
df['bin'] = pd.cut(df['y_prob'], bins=n_bins, include_lowest=True)
# Tính toán cho mỗi nhóm
grouped = df.groupby('bin').agg({
'y_true': ['count', 'sum'],
'y_prob': 'mean'
}).reset_index()
# Tính thống kê chi-square
chi_square = 0
for i in range(len(grouped)):
observed = grouped.iloc[i]['y_true']['sum']
expected = grouped.iloc[i]['y_true']['count'] * grouped.iloc[i]['y_prob']['mean']
n = grouped.iloc[i]['y_true']['count']
if expected > 0 and (n - expected) > 0:
chi_square += ((observed - expected)**2 / expected +
((n - observed) - (n - expected))**2 / (n - expected))
p_value = 1 - stats.chi2.cdf(chi_square, n_bins - 2)
return chi_square, p_value
chi_sq, p_val = hosmer_lemeshow_test(y, predicted_prob)
print(f"\nKiểm định Hosmer-Lemeshow:")
print(f"Chi-square: {chi_sq:.3f}")
print(f"P-value: {p_val:.3f}")
Tài liệu tham khảo
Để tìm hiểu sâu hơn về hồi quy logit và ứng dụng trong kinh tế lượng, tham khảo các nguồn sau:
- Gujarati, D.N. (2003). Basic Econometrics. McGraw-Hill.
- Hosmer, D.W., Lemeshow, S. (2013). Applied Logistic Regression. Wiley.
- IBM SPSS Statistics Documentation – Binary Logistic Regression
- Wooldridge, J.M. (2020). Introductory Econometrics: A Modern Approach. Cengage Learning.
Liên kết hữu ích:
- Hồi quy tuyến tính đa biến với SPSS
- Hồi quy thứ tự (Ordinal Regression)
- Kiểm định chi bình phương
- Các loại thang đo trong phân tích dữ liệu
Chú thích:
- Tùy theo dạng biến phụ thuộc mà ta có thể sử dụng các phương pháp hồi quy khác nhau: biến liên tục (hồi quy đa biến), biến thứ tự (hồi quy thứ tự), biến định danh (hồi quy logit đa biến hoặc phân tích phân tách).
- Phương pháp hợp lý cực đại (Maximum Likelihood) tính toán và chọn ước lượng sao cho xác suất quan sát được dữ liệu mẫu là lớn nhất.