Kiểm định T-test trung bình hai mẫu
Kiểm định t-test trung bình hai mẫu độc lập với SPSS

Tóm tắt: Kiểm định t-test trung bình hai mẫu độc lập là công cụ quan trọng trong thực hành kinh tế lượng, được sử dụng để so sánh giá trị trung bình của một biến liên tục giữa hai nhóm độc lập. Bài viết này hướng dẫn chi tiết cách thực hiện kiểm định bằng SPSS, từ kiểm tra các giả thiết cần thiết đến đọc hiểu kết quả đầu ra. Các bạn sẽ học được cách áp dụng kiểm định này trong phân tích dữ liệu kinh tế thực tế.
Giới thiệu
Nội dung chính
Trong nghiên cứu kinh tế và xã hội, chúng ta thường gặp các câu hỏi như: “Thu nhập trung bình của nam giới có cao hơn nữ giới không?”, “Điểm số trung bình của học sinh thành thị có khác biệt so với học sinh nông thôn không?”, hay “Hiệu quả đầu tư của các doanh nghiệp nhà nước có khác với doanh nghiệp tư nhân không?”. Để trả lời những câu hỏi này một cách khoa học, chúng ta cần sử dụng kiểm định t-test trung bình hai mẫu độc lập.
Khác với kiểm định t-test trung bình 1 mẫu được sử dụng để so sánh trung bình của một tổng thể với một giá trị cụ thể, kiểm định t-test trung bình hai mẫu độc lập cho phép chúng ta so sánh trung bình của hai nhóm khác nhau. Đây là một trong những công cụ cơ bản nhất trong thực hành kinh tế lượng mà mọi nhà nghiên cứu kinh tế cần nắm vững.
Xem thêm: Kiểm định tham số (Parametric tests)
Giả thiết của kiểm định t-test trung bình hai mẫu độc lập
Trước khi thực hiện kiểm định bằng SPSS, các bạn cần đảm bảo dữ liệu thỏa mãn các điều kiện sau:
- Biến phụ thuộc liên tục: Biến cần phân tích phải là biến liên tục (dạng khoảng hoặc tỉ lệ). Tham khảo bài viết các loại thang đo để hiểu rõ hơn.
- Biến độc lập phân loại: Biến nhóm phải là biến phân loại có đúng hai mức, ví dụ: giới tính (nam/nữ), khu vực (thành thị/nông thôn), loại hình doanh nghiệp (nhà nước/tư nhân).
- Tính độc lập của quan sát: Các quan sát trong từng nhóm và giữa các nhóm phải độc lập với nhau, không có mối liên hệ hoặc ảnh hưởng lẫn nhau.
- Không có điểm dị biệt: Dữ liệu không chứa các điểm dị biệt có thể làm sai lệch kết quả kiểm định.
- Phân phối chuẩn: Biến phụ thuộc phải có (hoặc xấp xỉ) phân phối chuẩn trong từng nhóm.
- Đồng nhất phương sai: Phương sai đồng nhất giữa hai nhóm.
Ví dụ thực tế từ kinh tế Việt Nam
Để minh họa cách thức thực hiện kiểm định, chúng ta sẽ sử dụng ví dụ về so sánh điểm số trung bình môn toán giữa học sinh nam và nữ. Đây là một vấn đề thực tế trong lĩnh vực giáo dục Việt Nam, giúp các bạn hiểu rõ ứng dụng của kiểm định t-test trong thực hành kinh tế lượng.
Trong bối cảnh giáo dục Việt Nam, việc đánh giá sự khác biệt về năng lực học tập giữa nam và nữ sinh luôn là chủ đề được quan tâm. Kết quả nghiên cứu không chỉ có ý nghĩa học thuật mà còn giúp hoạch định chính sách giáo dục phù hợp.
Dữ liệu mẫu
Chúng ta sử dụng bộ dữ liệu hsb2.sav với thông tin về 200 học sinh từ trung học trở xuống. Các biến chính trong bộ dữ liệu bao gồm:
- math: Điểm số môn toán (biến phụ thuộc)
- read: Điểm số môn đọc
- write: Điểm số môn viết
- female: Giới tính (0 = nam, 1 = nữ) – biến độc lập
- prog: Chương trình học
Câu hỏi nghiên cứu: Điểm trung bình môn toán giữa học sinh nam và nữ có khác biệt có ý nghĩa thống kê hay không?
Hướng dẫn thực hành chi tiết trên SPSS
Bước 1: Kiểm tra phân phối chuẩn
Trước khi thực hiện kiểm định chính, chúng ta cần kiểm tra giả thiết về phân phối chuẩn của biến math.
Thực hiện kiểm định Kolmogorov-Smirnov bằng cách:
- Vào menu Analyze → Nonparametric Tests → One Sample…
- Chọn tab Settings
- Tích chọn Test observed distribution against hypothesized (Kolmogorov-Smirnov test)
Kết quả kiểm định Kolmogorov-Smirnov:

Bước 2: Thực hiện kiểm định t-test trung bình 2 mẫu độc lập
Sau khi đã xác nhận dữ liệu thỏa mãn điều kiện, chúng ta tiến hành thực hiện kiểm định chính:
Bước 2.1: Truy cập menu kiểm định
Vào Analyze → Compare Means → Independent-Samples T Test…

Bước 2.2: Cấu hình biến cho kiểm định
- Đưa biến math vào khung Test Variable(s) (biến cần kiểm định)
- Đưa biến female vào khung Grouping Variable (biến nhóm)
- Nhấn nút Define Groups… để định nghĩa các nhóm
Bước 2.3: Định nghĩa nhóm
Trong cửa sổ Define Groups, thiết lập:
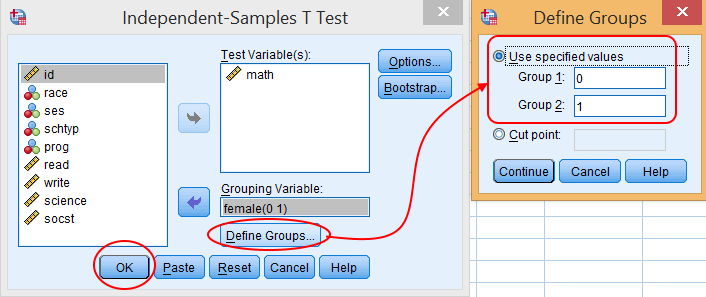
- Group 1: 0 (đại diện cho nam)
- Group 2: 1 (đại diện cho nữ)
Nhấn Continue để trở về cửa sổ chính, sau đó nhấn OK để thực hiện kiểm định.
Giải thích kết quả
Kết quả kiểm định t-test trung bình hai mẫu độc lập sẽ hiển thị như sau:

Phân tích bảng Group Statistics
Bảng đầu tiên Group Statistics cung cấp thống kê mô tả cho từng nhóm:
- Nhóm nam (N = 91): Điểm trung bình = 52.95, độ lệch chuẩn = 9.77
- Nhóm nữ (N = 109): Điểm trung bình = 52.39, độ lệch chuẩn = 9.25
- Chênh lệch: Nam có điểm trung bình cao hơn nữ 0.56 điểm
Phân tích bảng Independent Samples Test
Bảng thứ hai là kết quả chính của kiểm định:
Kiểm định Levene về đồng nhất phương sai:
Kết luận: Chưa đủ cơ sở để bác bỏ giả thuyết về đồng nhất phương sai. Do đó, chúng ta sử dụng kết quả ở dòng “Equal variances assumed“.
Kết quả kiểm định t-test:
- Thống kê t: t = 0.789
- Bậc tự do: df = 198
- Sig. (2-tailed): p = 0.432 > 0.05
- Mean Difference: 0.563
- 95% Confidence Interval: [-0.856, 1.982]
Kết luận nghiên cứu
Mặc dù điểm trung bình của nam cao hơn nữ 0.56 điểm, nhưng sự chênh lệch này có thể do ngẫu nhiên và không đủ lớn để có ý nghĩa thống kê.
Lưu ý và cảnh báo quan trọng
- Kích thước mẫu: Mẫu quá nhỏ có thể làm giảm hiệu năng (power) của kiểm định
- Outliers: Luôn kiểm tra và xử lý các điểm dị biệt trước khi phân tích
- Giả thiết: Đảm bảo tất cả các giả thiết được thỏa mãn
- Practical significance: Phân biệt giữa ý nghĩa thống kê và ý nghĩa thực tiễn
- Không kiểm tra giả thiết phân phối chuẩn
- Sử dụng sai kết quả khi vi phạm giả thiết đồng nhất phương sai
- Diễn giải sai ý nghĩa của giá trị p
- Không báo cáo khoảng tin cậy
Ứng dụng trong nghiên cứu kinh tế
Kiểm định t-test trung bình hai mẫu độc lập có nhiều ứng dụng trong thực hành kinh tế lượng:
- Nghiên cứu lao động: So sánh mức lương trung bình giữa nam và nữ
- Phân tích thị trường: So sánh doanh thu trung bình giữa các vùng miền
- Đánh giá chính sách: So sánh hiệu quả của các can thiệp chính sách
- Nghiên cứu tiêu dùng: So sánh chi tiêu trung bình giữa các nhóm dân cư
- Phân tích tài chính: So sánh tỷ suất sinh lời giữa các loại hình đầu tư
Tổng kết
Kiểm định t-test trung bình hai mẫu độc lập là một công cụ quan trọng trong thực hành kinh tế lượng, giúp các nhà nghiên cứu đưa ra kết luận khoa học về sự khác biệt giữa hai nhóm. Việc thành thạo kỹ thuật này trên SPSS sẽ hỗ trợ đắc lực cho công tác nghiên cứu và phân tích dữ liệu.
Qua ví dụ thực tế về so sánh điểm toán giữa nam và nữ sinh, các bạn đã học được cách:
- Kiểm tra các giả thiết cần thiết
- Thực hiện kiểm định trên SPSS một cách chi tiết
- Đọc và diễn giải kết quả chính xác
- Đưa ra kết luận khoa học có căn cứ
Key Points:
- T-test trung bình hai mẫu độc lập dùng để so sánh trung bình của hai nhóm riêng biệt
- Dữ liệu phải thỏa mãn 6 giả thiết cơ bản về tính liên tục, độc lập, phân phối chuẩn và đồng nhất phương sai
- SPSS cung cấp công cụ thực hiện kiểm định một cách trực quan và dễ dàng
- Kết quả bao gồm kiểm định Levene, thống kê t, giá trị p và khoảng tin cậy
- Cần phân biệt rõ ý nghĩa thống kê và ý nghĩa thực tiễn trong diễn giải kết quả
Phụ lục: Code trên các phần mềm khác
SPSS Syntax
SPSS Syntax (.sps)
* Kiểm định t-test trung bình 2 mẫu độc lập bằng SPSS Syntax
* Tác giả: Thực hành kinh tế lượng
* Dữ liệu: hsb2.sav
* Mở file dữ liệu
GET FILE='/data/hsb2.sav'.
* Kiểm tra phân phối chuẩn bằng Kolmogorov-Smirnov
NPAR TESTS
/K-S(NORMAL)=math
/MISSING ANALYSIS.
* Thực hiện t-test trung bình 2 mẫu độc lập
T-TEST GROUPS=female(0 1)
/MISSING=ANALYSIS
/VARIABLES=math
/CRITERIA=CI(.95).
* Thống kê mô tả theo nhóm
MEANS TABLES=math BY female
/CELLS=MEAN STDDEV COUNT.
Stata
Stata (.do)
// Kiểm định t-test trung bình 2 mẫu độc lập bằng Stata
// Tác giả: Thực hành kinh tế lượng
// Dữ liệu: hsb2.dta
* Mở file dữ liệu
use "hsb2.dta", clear
* Mô tả dữ liệu
describe math female
* Thống kê mô tả theo nhóm
tabstat math, by(female) statistics(mean sd count)
* Kiểm tra phân phối chuẩn bằng Shapiro-Wilk test
by female, sort: swilk math
* Kiểm định t-test trung bình 2 mẫu độc lập
ttest math, by(female)
* Kiểm định đồng nhất phương sai (Levene's test)
robvar math, by(female)
* Thống kê mô tả chi tiết
by female: summarize math, detail
R
R (.R)
# Kiểm định t-test trung bình 2 mẫu độc lập bằng R
# Tác giả: Thực hành kinh tế lượng
# Dữ liệu: hsb2.csv
# Cài đặt và load các package cần thiết
if (!require(car)) install.packages("car")
if (!require(psych)) install.packages("psych")
library(car)
library(psych)
# Đọc dữ liệu
data <- read.csv("hsb2.csv")
# Kiểm tra cấu trúc dữ liệu
str(data)
head(data)
# Chuyển đổi biến female thành factor
data$female <- factor(data$female, levels = c(0, 1), labels = c("Nam", "Nữ"))
# Thống kê mô tả theo nhóm
describeBy(data$math, data$female)
# Kiểm tra phân phối chuẩn bằng Shapiro-Wilk test
by(data$math, data$female, shapiro.test)
# Kiểm định đồng nhất phương sai bằng Levene's test
leveneTest(math ~ female, data = data)
# Thực hiện t-test trung bình 2 mẫu độc lập
t_test_result <- t.test(math ~ female, data = data, var.equal = TRUE)
print(t_test_result)
# Thống kê mô tả chi tiết
aggregate(math ~ female, data = data,
FUN = function(x) c(mean = mean(x), sd = sd(x), n = length(x)))
# Vẽ boxplot để so sánh trực quan
boxplot(math ~ female, data = data,
main = "So sánh điểm toán theo giới tính",
xlab = "Giới tính", ylab = "Điểm toán",
col = c("lightblue", "pink"))
Python
Python (.py)
# Kiểm định t-test trung bình 2 mẫu độc lập bằng Python
# Tác giả: Thực hành kinh tế lượng
# Dữ liệu: hsb2.csv
import pandas as pd
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import levene, shapiro, ttest_ind
# Đọc dữ liệu
data = pd.read_csv('hsb2.csv')
# Kiểm tra cấu trúc dữ liệu
print("Thông tin dữ liệu:")
print(data.info())
print("\n5 dòng đầu:")
print(data.head())
# Tạo biến nhóm
data['gender'] = data['female'].map({0: 'Nam', 1: 'Nữ'})
# Thống kê mô tả theo nhóm
print("\nThống kê mô tả theo giới tính:")
print(data.groupby('gender')['math'].describe())
# Tách dữ liệu theo nhóm
math_nam = data[data['female'] == 0]['math']
math_nu = data[data['female'] == 1]['math']
# Kiểm tra phân phối chuẩn bằng Shapiro-Wilk test
print("\nKiểm định phân phối chuẩn (Shapiro-Wilk):")
stat_nam, p_nam = shapiro(math_nam)
stat_nu, p_nu = shapiro(math_nu)
print(f"Nam: W = {stat_nam:.4f}, p-value = {p_nam:.4f}")
print(f"Nữ: W = {stat_nu:.4f}, p-value = {p_nu:.4f}")
# Kiểm định đồng nhất phương sai bằng Levene's test
print("\nKiểm định đồng nhất phương sai (Levene):")
stat_levene, p_levene = levene(math_nam, math_nu)
print(f"F = {stat_levene:.4f}, p-value = {p_levene:.4f}")
# Thực hiện t-test trung bình 2 mẫu độc lập
print("\nKết quả t-test trung bình 2 mẫu độc lập:")
stat_t, p_t = ttest_ind(math_nam, math_nu, equal_var=True)
print(f"t-statistic = {stat_t:.4f}")
print(f"p-value = {p_t:.4f}")
# Tính khoảng tin cậy cho hiệu số trung bình
mean_diff = np.mean(math_nam) - np.mean(math_nu)
n1, n2 = len(math_nam), len(math_nu)
pooled_std = np.sqrt(((n1-1)*np.var(math_nam, ddof=1) + (n2-1)*np.var(math_nu, ddof=1))/(n1+n2-2))
se_diff = pooled_std * np.sqrt(1/n1 + 1/n2)
df = n1 + n2 - 2
t_critical = stats.t.ppf(0.975, df)
ci_lower = mean_diff - t_critical * se_diff
ci_upper = mean_diff + t_critical * se_diff
print(f"\nChênh lệch trung bình: {mean_diff:.4f}")
print(f"95% Confidence Interval: [{ci_lower:.4f}, {ci_upper:.4f}]")
# Vẽ biểu đồ so sánh
plt.figure(figsize=(12, 5))
# Boxplot
plt.subplot(1, 2, 1)
sns.boxplot(x='gender', y='math', data=data)
plt.title('Boxplot điểm toán theo giới tính')
plt.ylabel('Điểm toán')
# Histogram
plt.subplot(1, 2, 2)
plt.hist(math_nam, alpha=0.7, label='Nam', bins=15)
plt.hist(math_nu, alpha=0.7, label='Nữ', bins=15)
plt.xlabel('Điểm toán')
plt.ylabel('Tần số')
plt.title('Phân phối điểm toán theo giới tính')
plt.legend()
plt.tight_layout()
plt.show()
# Kết luận
print(f"\nKết luận:")
if p_t < 0.05:
print("Có sự khác biệt có ý nghĩa thống kê về điểm toán giữa nam và nữ (p < 0.05)")
else:
print("Không có sự khác biệt có ý nghĩa thống kê về điểm toán giữa nam và nữ (p ≥ 0.05)")
Tài liệu tham khảo
- Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics. 5th Edition. SAGE Publications.
- Pallant, J. (2020). SPSS Survival Manual: A Step by Step Guide to Data Analysis Using IBM SPSS. 7th Edition. McGraw-Hill Education.
- IBM Corporation. (2021). IBM SPSS Statistics Base 28. IBM SPSS Statistics Documentation.
- Hoàng Trọng & Chu Nguyễn Mộng Ngọc. (2019). Phân tích dữ liệu nghiên cứu với SPSS. NXB Hồng Đức.
- Nguyễn Khánh Trung. (2020). Thực hành kinh tế lượng với phần mềm thống kê. NXB Thống kê.