T-test trung bình một mẫu
Kiểm định t-test trung bình một mẫu trong thực hành kinh tế lượng với SPSS

Tóm tắt: Kiểm định t-test trung bình một mẫu là phương pháp thống kê quan trọng trong thực hành kinh tế lượng, cho phép kiểm tra xem trung bình của một biến có khác ý nghĩa thống kê với giá trị giả định ban đầu hay không. Bài viết này hướng dẫn chi tiết cách thực hiện kiểm định trên SPSS thông qua giao diện người dùng, kèm theo phân tích kết quả và các đoạn mã tương đương trong Stata, R và Python để hỗ trợ việc học tập đa nền tảng.
Giới thiệu về kiểm định t-test trung bình một mẫu
Nội dung chính
- Giới thiệu về kiểm định t-test trung bình một mẫu
- Giả thiết thống kê và công thức toán học
- Điều kiện và giả định của kiểm định
- Ví dụ thực tế với dữ liệu mẫu
- Hướng dẫn thực hành chi tiết trên SPSS
- Phân tích và diễn giải kết quả
- Lưu ý quan trọng và cảnh báo
- Tổng kết
- Phụ lục: Code tương đương trong các phần mềm khác
- Tài liệu tham khảo
Xem thêm: Kiểm định tham số (Parametric tests)
Ứng dụng trong bối cảnh kinh tế Việt Nam
Trong thực hành kinh tế lượng tại Việt Nam, kiểm định này thường được áp dụng để:
- Kiểm tra mức lương trung bình của một ngành có đạt chuẩn quy định hay không
- Đánh giá hiệu quả chính sách kinh tế thông qua so sánh các chỉ số trước và sau khi áp dụng
- Phân tích kết quả học tập của sinh viên so với điểm chuẩn đầu vào
- Kiểm định giả thuyết về tỷ suất sinh lợi của các khoản đầu tư
Ví dụ cụ thể: Giả sử Bộ Giáo dục và Đào tạo quy định điểm trung bình môn Toán của học sinh THPT phải đạt tối thiểu 5.0 điểm. Một trường muốn kiểm tra xem điểm trung bình môn Toán của học sinh trường mình có đạt tiêu chuẩn này hay không. Đây chính là bài toán điển hình cho kiểm định giả thuyết bằng t-test một mẫu.
Giả thiết thống kê và công thức toán học
Kiểm định t-test trung bình một mẫu được phát biểu dưới dạng giả thuyết thống kê như sau:
$${H_0}: \mu = \mu_0$$
Trong đó:
- \(\mu\): trung bình tổng thể
- \(\mu_0\): giá trị giả thiết ban đầu
Các giả thuyết thay thế có thể là:
$$\begin{array}{l}{H_1}: \mu \neq \mu_0 \text{ (kiểm định hai phía)}\\{H_1}: \mu > \mu_0 \text{ (kiểm định một phía – phải)}\\{H_1}: \mu < \mu_0 \text{ (kiểm định một phía – trái)}\end{array}$$
Công thức thống kê kiểm định
Thống kê kiểm định t được tính theo công thức:
$$t = \frac{\bar{x} – \mu_0}{s/\sqrt{n}}$$
Trong đó:
- \(\bar{x}\): trung bình mẫu
- \(s\): độ lệch chuẩn mẫu
- \(n\): kích thước mẫu
- \(\mu_0\): giá trị giả thiết
Xem thêm t-test trung bình một mẫu
Điều kiện và giả định của kiểm định
Để áp dụng kiểm định t-test trung bình một mẫu trong thực hành kinh tế lượng, dữ liệu cần thỏa mãn các điều kiện sau:
- Tính độc lập: Các quan sát trong mẫu phải độc lập với nhau
- Phân phối chuẩn: Dữ liệu có phân phối chuẩn hoặc gần chuẩn, hoặc kích thước mẫu đủ lớn (n ≥ 30)
- Thang đo: Biến phải là biến định lượng (thang đo khoảng hoặc tỉ lệ)
- Không có outlier: Dữ liệu không chứa các giá trị ngoại lai nghiêm trọng
Ví dụ thực tế với dữ liệu mẫu
Trong bài hướng dẫn này, chúng ta sẽ sử dụng bộ dữ liệu hsb2.sav – một bộ dữ liệu chuẩn trong thực hành kinh tế lượng. Bộ dữ liệu này chứa thông tin về 200 học sinh trung học với các biến chính:
- Điểm số các môn: toán (math), đọc (read), viết (write)
- Thông tin học tập: chương trình học (prog)
- Thông tin cá nhân: giới tính (female)
- Các biến nhân khẩu học khác
Câu hỏi nghiên cứu
Giả sử theo tiêu chuẩn giáo dục quốc gia, điểm trung bình môn Toán của học sinh trung học phải đạt ít nhất 50 điểm. Chúng ta muốn kiểm tra xem điểm trung bình môn Toán của các học sinh trong mẫu có khác biệt ý nghĩa thống kê với mức chuẩn 50 điểm này hay không.
Giả thuyết thống kê được phát biểu cụ thể như sau:
- \({H_0}\): \(\mu_{math} = 50\) (Điểm trung bình môn Toán bằng 50)
- \({H_1}\): \(\mu_{math} \neq 50\) (Điểm trung bình môn Toán khác 50)
Hướng dẫn thực hành chi tiết trên SPSS
Phần này sẽ hướng dẫn các bạn từng bước thực hiện kiểm định t-test trung bình một mẫu trong SPSS thông qua giao diện đồ họa. Đây là cách tiếp cận phù hợp nhất cho những ai mới bắt đầu học thực hành kinh tế lượng.
Để bắt đầu quá trình kiểm định, các bạn thực hiện theo trình tự sau:
Vào Analyze → Compare Means → One-Sample T Test…

Bước 2: Cấu hình kiểm định
Sau khi thực hiện bước 1, cửa sổ One-Sample T Test sẽ mở ra. Tại đây, các bạn cần:
- Đưa biến cần kiểm định (math) vào khung Test Variable(s)
- Thiết lập giá trị cần so sánh (trong trường hợp này là 50) vào ô Test Value
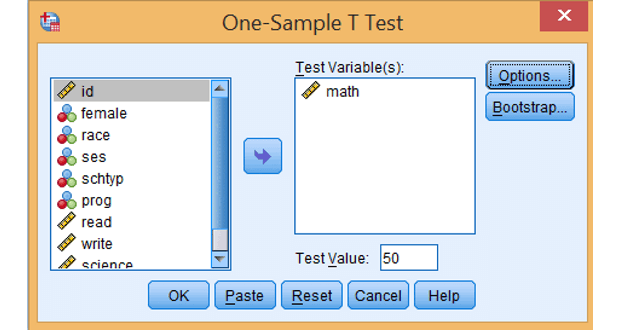
- Test Variable(s): Chọn biến math từ danh sách bên trái và di chuyển sang khung này
- Test Value: Nhập giá trị 50 – đây là giá trị \(\mu_0\) trong giả thuyết H0
- Options: Có thể điều chỉnh mức tin cậy (mặc định 95%) nếu cần thiết
Bước 3: Thực hiện kiểm định
Sau khi hoàn tất cấu hình, bấm OK để SPSS thực hiện kiểm định. Phần mềm sẽ tự động tính toán thống kê t, bậc tự do, và p-value tương ứng.
Phân tích và diễn giải kết quả
Kết quả kiểm định t-test trung bình một mẫu sẽ được hiển thị trong hai bảng output của SPSS:

Phân tích bảng thống kê mô tả
Bảng đầu tiên (One-Sample Statistics) cung cấp thông tin mô tả về biến math:
- N: Kích thước mẫu (200 học sinh)
- Mean: Điểm trung bình môn Toán = 52.645
- Std. Deviation: Độ lệch chuẩn của mẫu
- Std. Error Mean: Sai số chuẩn của trung bình mẫu
Phân tích bảng kiểm định
Bảng thứ hai (One-Sample Test) chứa kết quả kiểm định chính:
- t: Giá trị thống kê t tính được
- df: Bậc tự do (n-1 = 199)
- Sig. (2-tailed): P-value cho kiểm định hai phía
- Mean Difference: Hiệu số giữa trung bình mẫu và giá trị kiểm định (52.645 – 50 = 2.645)
- 95% Confidence Interval: Khoảng tin cậy 95% cho hiệu số trung bình
Diễn giải kết quả cụ thể
Từ kết quả phân tích, chúng ta có thể rút ra những kết luận sau:
- Điểm trung bình mẫu: 52.645 điểm
- Hiệu số so với tiêu chuẩn: +2.645 điểm
- Ý nghĩa thống kê: p < 0.01 (có ý nghĩa ở mức 1%)
- Kết luận: Điểm trung bình môn Toán của học sinh cao hơn tiêu chuẩn 50 điểm một cách có ý nghĩa thống kê
Cụ thể, với p-value < 0.01, chúng ta có đủ bằng chứng thống kê để bác bỏ giả thuyết H0 ở mức ý nghĩa 1%. Điều này có nghĩa là điểm trung bình môn Toán của các học sinh trong mẫu khác biệt ý nghĩa thống kê với mức chuẩn 50 điểm, và cụ thể là cao hơn 50 điểm.
Ý nghĩa thực tiễn
Trong bối cảnh thực hành kinh tế lượng tại Việt Nam, kết quả này cho thấy:
- Chất lượng giáo dục môn Toán tại trường này vượt trội so với tiêu chuẩn quốc gia
- Có thể áp dụng phương pháp giảng dạy của trường này cho các trường khác
- Cần nghiên cứu thêm về các yếu tố góp phần vào thành tích này
- Kết quả có thể được sử dụng làm căn cứ cho việc điều chỉnh chính sách giáo dục
Lưu ý quan trọng và cảnh báo
Khi thực hiện kiểm định t-test trung bình một mẫu trong thực hành kinh tế lượng, các bạn cần chú ý những điểm sau:
Về điều kiện áp dụng
- Biểu đồ Q-Q plot
- Kiểm định Shapiro-Wilk (cho n < 50)
- Kiểm định Kolmogorov-Smirnov (cho n ≥ 50)
Về diễn giải kết quả
- Ý nghĩa thống kê vs. thực tiễn: Kết quả có ý nghĩa thống kê không nhất thiết có ý nghĩa thực tiễn
- Kích thước hiệu ứng: Cần xem xét độ lớn của hiệu số trung bình, không chỉ p-value
- Tính tổng quát: Kết quả chỉ áp dụng cho tổng thể mà mẫu đại diện
- Nhân quả: Kiểm định chỉ cho biết mối quan hệ, không chứng minh nhân quả
Các lỗi thường gặp
- Không kiểm tra giả định phân phối chuẩn
- Diễn giải sai ý nghĩa của p-value
- Nhầm lẫn giữa kiểm định một phía và hai phía
- Không xem xét mức độ ảnh hưởng (effect size)
- Áp dụng cho dữ liệu không đủ điều kiện
Mở rộng phân tích
Sau khi có kết quả t-test, các bạn có thể thực hiện thêm:
- Tính toán Cohen’s d: Đo lường kích thước hiệu ứng
- Bootstrap confidence interval: Ước lượng khoảng tin cậy bằng phương pháp bootstrap
- Power analysis: Phân tích hiệu năng (power) của kiểm định
- Sensitivity analysis: Kiểm tra tính nhạy cảm của kết quả với các giả định
Tổng kết
Kiểm định t-test trung bình một mẫu là một công cụ mạnh mẽ và thiết yếu trong thực hành kinh tế lượng. Thông qua việc sử dụng SPSS, chúng ta có thể dễ dàng kiểm tra xem trung bình của một biến có khác biệt ý nghĩa thống kê với một giá trị chuẩn hay không.
Trong ví dụ về điểm môn Toán, kết quả kiểm định cho thấy điểm trung bình của học sinh (52.645) cao hơn có ý nghĩa thống kê so với tiêu chuẩn 50 điểm (p < 0.01). Điều này có nghĩa là chúng ta có thể tin tưởng rằng chất lượng giáo dục môn Toán tại trường này vượt trội so với tiêu chuẩn quốc gia.
Tuy nhiên, cần nhớ rằng kết quả thống kê chỉ là một phần của câu chuyện. Trong thực hành kinh tế lượng, việc kết hợp phân tích định lượng với hiểu biết về bối cảnh thực tế là điều cần thiết để đưa ra những kết luận có ý nghĩa và hữu ích.
Điểm chính cần nhớ:
- T-test một mẫu phù hợp khi muốn so sánh trung bình mẫu với giá trị chuẩn
- Dữ liệu cần có phân phối chuẩn hoặc kích thước mẫu đủ lớn (n ≥ 30)
- P-value < α: bác bỏ H0 (trung bình khác giá trị chuẩn)
- P-value ≥ α: không bác bỏ H0 (chưa có bằng chứng về sự khác biệt)
- Cần xem xét cả ý nghĩa thống kê và ý nghĩa thực tiễn của kết quả
- Kết quả chỉ áp dụng cho tổng thể mà mẫu đại diện
Phụ lục: Code tương đương trong các phần mềm khác
Để hỗ trợ các bạn làm quen với nhiều công cụ phân tích khác nhau trong thực hành kinh tế lượng, phần này cung cấp code tương đương cho kiểm định t-test trung bình một mẫu trong SPSS Syntax, Stata, R và Python.
SPSS Syntax
SPSS Syntax (.sps)
* Mở file dữ liệu
GET FILE='/data/hsb2.sav'.
* Kiểm tra thống kê mô tả trước khi thực hiện kiểm định
DESCRIPTIVES VARIABLES=math
/STATISTICS=MEAN STDDEV MIN MAX.
* Kiểm tra tính phân phối chuẩn
EXAMINE VARIABLES=math
/PLOT BOXPLOT STEMLEAF NPPLOT
/COMPARE GROUPS
/STATISTICS DESCRIPTIVES
/CINTERVAL 95
/MISSING LISTWISE
/NOTOTAL.
* Thực hiện kiểm định t-test trung bình một mẫu
* H0: mu = 50, H1: mu ≠ 50
T-TEST
/TESTVAL=50
/MISSING=ANALYSIS
/VARIABLES=math
/CRITERIA=CI(.95).
* Hiển thị kết quả bổ sung
MEANS TABLES=math
/CELLS=MEAN COUNT STDDEV MIN MAX.
Stata
Stata (.do)
* Mở file dữ liệu
use "/data/hsb2.dta", clear
* Kiểm tra thống kê mô tả
summarize math, detail
* Kiểm tra tính phân phối chuẩn
* Shapiro-Wilk test (cho n < 5000)
swilk math
* Histogram và normal probability plot
histogram math, normal
qnorm math
* Thực hiện kiểm định t-test trung bình một mẫu
* H0: mu = 50, H1: mu ≠ 50
ttest math == 50
* Tính toán confidence interval cho trung bình
ci means math, level(95)
* Hiển thị thống kê bổ sung
tabstat math, statistics(mean sd min max count) columns(statistics)
* Tính toán effect size (Cohen's d)
scalar mu0 = 50
scalar xbar = r(mean)
scalar s = r(sd)
scalar n = r(N)
scalar cohens_d = (xbar - mu0) / s
display "Cohen's d = " cohens_d
R
R (.R)
# Cài đặt và tải các package cần thiết
if (!require(foreign)) install.packages("foreign")
if (!require(psych)) install.packages("psych")
if (!require(car)) install.packages("car")
if (!require(effectsize)) install.packages("effectsize")
library(foreign)
library(psych)
library(car)
library(effectsize)
# Đọc dữ liệu SPSS
data <- read.spss("/data/hsb2.sav", to.data.frame = TRUE)
# Kiểm tra cấu trúc dữ liệu
str(data)
head(data)
# Thống kê mô tả cho biến math
describe(data$math)
summary(data$math)
# Kiểm tra tính phân phối chuẩn
# Shapiro-Wilk test
shapiro.test(data$math)
# Q-Q plot
qqnorm(data$math)
qqline(data$math)
# Histogram với đường cong chuẩn
hist(data$math, probability = TRUE,
main = "Histogram điểm Toán với đường cong chuẩn",
xlab = "Điểm Toán", ylab = "Mật độ")
curve(dnorm(x, mean = mean(data$math), sd = sd(data$math)), add = TRUE, col = "red")
# Thực hiện kiểm định t-test trung bình một mẫu
# H0: mu = 50, H1: mu ≠ 50
t_test_result <- t.test(data$math, mu = 50)
print(t_test_result)
# Trích xuất thông tin chi tiết
cat("Thống kê t:", t_test_result$statistic, "\n")
cat("Bậc tự do:", t_test_result$parameter, "\n")
cat("p-value:", t_test_result$p.value, "\n")
cat("Khoảng tin cậy 95%:", t_test_result$conf.int, "\n")
cat("Trung bình mẫu:", t_test_result$estimate, "\n")
# Tính toán Cohen's d (effect size)
cohens_d <- cohens_d(data$math, mu = 50)
print(cohens_d)
# Diễn giải kết quả
alpha <- 0.05
if (t_test_result$p.value < alpha) {
cat("\nKết luận: p-value (", round(t_test_result$p.value, 4), ") < α (", alpha, ")\n") cat("Bác bỏ H0. Điểm trung bình môn Toán khác 50 một cách có ý nghĩa thống kê.\n") if (t_test_result$estimate > 50) {
cat("Cụ thể: Điểm trung bình cao hơn 50.\n")
} else {
cat("Cụ thể: Điểm trung bình thấp hơn 50.\n")
}
} else {
cat("\nKết luận: p-value (", round(t_test_result$p.value, 4), ") ≥ α (", alpha, ")\n")
cat("Không bác bỏ H0. Chưa có bằng chứng về sự khác biệt.\n")
}
# Tạo bảng tóm tắt kết quả
result_summary <- data.frame(
"Thống kê" = c("N", "Trung bình", "Độ lệch chuẩn", "t-statistic",
"df", "p-value", "Cohen's d"),
"Giá trị" = c(length(data$math),
round(mean(data$math), 3),
round(sd(data$math), 3),
round(t_test_result$statistic, 3),
t_test_result$parameter,
round(t_test_result$p.value, 4),
round(as.numeric(cohens_d), 3))
)
print(result_summary)
Python
Python (.py)
# Import các thư viện cần thiết
import pandas as pd
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import shapiro
import pyreadstat
# Thiết lập để hiển thị tiếng Việt
plt.rcParams['font.family'] = 'DejaVu Sans'
# Đọc dữ liệu SPSS
data, meta = pyreadstat.read_sav('/data/hsb2.sav')
# Kiểm tra cấu trúc dữ liệu
print("Thông tin cơ bản về dữ liệu:")
print(data.info())
print("\nThống kê mô tả cho biến math:")
print(data['math'].describe())
# Kiểm tra tính phân phối chuẩn
# Shapiro-Wilk test
shapiro_stat, shapiro_p = shapiro(data['math'])
print(f"\nKiểm định Shapiro-Wilk:")
print(f"Thống kê: {shapiro_stat:.4f}")
print(f"p-value: {shapiro_p:.4f}")
# Vẽ biểu đồ kiểm tra tính chuẩn
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# Histogram
axes[0].hist(data['math'], bins=20, density=True, alpha=0.7, color='skyblue')
axes[0].set_title('Histogram điểm Toán')
axes[0].set_xlabel('Điểm Toán')
axes[0].set_ylabel('Mật độ')
# Thêm đường cong chuẩn
x = np.linspace(data['math'].min(), data['math'].max(), 100)
axes[0].plot(x, stats.norm.pdf(x, data['math'].mean(), data['math'].std()),
'r-', label='Phân phối chuẩn')
axes[0].legend()
# Q-Q plot
stats.probplot(data['math'], dist="norm", plot=axes[1])
axes[1].set_title('Q-Q Plot')
plt.tight_layout()
plt.show()
# Thực hiện kiểm định t-test trung bình một mẫu
# H0: mu = 50, H1: mu ≠ 50
mu0 = 50
t_stat, p_value = stats.ttest_1samp(data['math'], mu0)
# Tính toán thông tin bổ sung
n = len(data['math'])
df = n - 1
sample_mean = data['math'].mean()
sample_std = data['math'].std(ddof=1)
se_mean = sample_std / np.sqrt(n)
# Tính confidence interval
confidence_level = 0.95
alpha = 1 - confidence_level
t_critical = stats.t.ppf(1 - alpha/2, df)
margin_error = t_critical * se_mean
ci_lower = sample_mean - margin_error
ci_upper = sample_mean + margin_error
# Tính Cohen's d (effect size)
cohens_d = (sample_mean - mu0) / sample_std
# Hiển thị kết quả
print(f"\nKết quả kiểm định t-test trung bình một mẫu:")
print(f"{'='*50}")
print(f"Kích thước mẫu (n): {n}")
print(f"Trung bình mẫu: {sample_mean:.3f}")
print(f"Độ lệch chuẩn mẫu: {sample_std:.3f}")
print(f"Sai số chuẩn: {se_mean:.3f}")
print(f"Giá trị kiểm định (μ₀): {mu0}")
print(f"Hiệu số (x̄ - μ₀): {sample_mean - mu0:.3f}")
print(f"\nThống kê kiểm định:")
print(f"t-statistic: {t_stat:.4f}")
print(f"Bậc tự do: {df}")
print(f"p-value (hai phía): {p_value:.4f}")
print(f"Khoảng tin cậy 95%: [{ci_lower:.3f}, {ci_upper:.3f}]")
print(f"Cohen's d: {cohens_d:.3f}")
# Diễn giải kết quả
alpha = 0.05
print(f"\nDiễn giải kết quả (α = {alpha}):")
print(f"{'='*50}")
if p_value < alpha:
print(f"p-value ({p_value:.4f}) < α ({alpha})") print("❌ Bác bỏ H₀") print("✅ Có bằng chứng thống kê cho thấy điểm trung bình môn Toán khác 50") if sample_mean > mu0:
print(f"📈 Điểm trung bình ({sample_mean:.3f}) cao hơn tiêu chuẩn ({mu0})")
else:
print(f"📉 Điểm trung bình ({sample_mean:.3f}) thấp hơn tiêu chuẩn ({mu0})")
else:
print(f"p-value ({p_value:.4f}) ≥ α ({alpha})")
print("✅ Không bác bỏ H₀")
print("❌ Chưa có bằng chứng thống kê về sự khác biệt")
# Đánh giá effect size
print(f"\nĐánh giá kích thước hiệu ứng (Cohen's d = {cohens_d:.3f}):")
if abs(cohens_d) < 0.2:
effect_size = "nhỏ"
elif abs(cohens_d) < 0.5:
effect_size = "trung bình"
elif abs(cohens_d) < 0.8:
effect_size = "lớn"
else:
effect_size = "rất lớn"
print(f"Kích thước hiệu ứng: {effect_size}")
# Tạo bảng tóm tắt
summary_df = pd.DataFrame({
'Thống kê': ['N', 'Trung bình', 'Độ lệch chuẩn', 'Sai số chuẩn',
't-statistic', 'Bậc tự do', 'p-value', "Cohen's d"],
'Giá trị': [n, f"{sample_mean:.3f}", f"{sample_std:.3f}", f"{se_mean:.3f}",
f"{t_stat:.4f}", df, f"{p_value:.4f}", f"{cohens_d:.3f}"]
})
print(f"\nBảng tóm tắt kết quả:")
print(summary_df.to_string(index=False))
# Lưu kết quả vào file (tùy chọn)
# summary_df.to_csv('t_test_results.csv', index=False)
Tài liệu tham khảo
Để nắm vững hơn về kiểm định t-test trung bình một mẫu trong thực hành kinh tế lượng, các bạn có thể tham khảo:
- IBM SPSS Statistics Documentation – Compare Means Procedures
- Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics (5th ed.). Sage Publications
- Gujarati, D. N., Porter, D. C., & Gunasekar, S. (2017). Basic Econometrics (5th ed.). McGraw-Hill Education
- Wooldridge, J. M. (2020). Introductory Econometrics: A Modern Approach (7th ed.). Cengage Learning
- Newbold, P., Carlson, W. L., & Thorne, B. (2019). Statistics for Business and Economics (9th ed.). Pearson
- Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (2nd ed.). Lawrence Erlbaum Associates