Phân tích phương sai đa biến một chiều
Hướng dẫn thực hiện phân tích MANOVA một chiều trên SPSS

Tóm tắt: MANOVA một chiều là kỹ thuật phân tích phương sai đa biến được sử dụng để kiểm tra sự khác biệt về giá trị trung bình của nhiều biến phụ thuộc liên tục giữa hai hoặc nhiều nhóm độc lập. Khác với ANOVA truyền thống chỉ xử lý một biến phụ thuộc, MANOVA cho phép phân tích đồng thời nhiều biến kết quả, tăng cường khả năng phát hiện sự khác biệt có ý nghĩa thống kê.
Giới thiệu về MANOVA một chiều
Nội dung chính
- Giới thiệu về MANOVA một chiều
- Ví dụ thực tế từ giáo dục Việt Nam
- Giả định của phương pháp MANOVA
- Thực hành phân tích MANOVA trên SPSS
- Code tương đương trong các phần mềm khác
- Hướng dẫn thực hành với Python
- Đọc kết quả phân tích MANOVA
- Lưu ý quan trọng và khuyến nghị
- Ứng dụng thực tế trong nghiên cứu kinh tế Việt Nam
- Tổng kết
MANOVA một chiều là viết tắt của One-way Multivariate Analysis Of Variance hay còn gọi là phân tích phương sai đa biến một chiều. Phân tích MANOVA một chiều là một phép phân tích phương sai được sử dụng để xem liệu có sự khác nhau về giá trị trung bình của các biến phụ thuộc theo hai hay nhiều nhóm của biến độc lập.
Về mặt này, nó khác so với phân tích phương sai một chiều (One-way ANOVA) ở chỗ ANOVA chỉ so sánh sự khác nhau với chỉ một biến phụ thuộc.
Nói một cách đơn giản: MANOVA là một ANOVA cho nhiều biến phụ thuộc. ANOVA kiểm tra sự khác nhau về giá trị trung bình của một biến phụ thuộc, còn MANOVA thì kiểm tra sự khác nhau về giá trị trung bình cho nhiều biến phụ thuộc.
Ví dụ thực tế từ giáo dục Việt Nam
Các sinh viên tại một trường đại học với 3 chương trình học khác nhau (tổng quát, hàn lâm, hướng nghiệp). Nhà trường muốn biết liệu có sự khác về kết quả học tập ở ba chương trình này không. Nhà trường lựa chọn ngẫu nhiên 200 mẫu (bao gồm 45 sinh viên theo học chương trình tổng quát, 105 sinh viên theo học chương trình hàn lâm và 50 sinh viên theo học chương trình hướng nghiệp).
Kết quả học tập của họ được đánh giá qua điểm số của hai môn khoa học và xã hội. Như vậy, theo ý nghĩa của phân tích MANOVA một chiều thì mô hình phân tích gồm hai biến phụ thuộc là biến điểm môn khoa học (science) và điểm môn xã hội (socst) và biến độc lập dạng phân loại là biến chương trình học (prog) với ba giá trị là chương trình tổng quát, chương trình hàn lâm và chương trình hướng nghiệp.
Câu hỏi nghiên cứu: Có sự khác nhau về giá trị trung bình của science và socst theo prog hay không? Chúng ta có thể sử dụng bộ dữ liệu hsb.sav để trả lời câu hỏi này.
Giả định của phương pháp MANOVA
Trước khi tiến hành phân tích cần kiểm tra các giả định của phương pháp. Phương pháp phân tích MANOVA 1 chiều dữ liệu phải thỏa mãn các giả thuyết sau:
- Tính chất biến phụ thuộc: Hai hay nhiều biến phụ thuộc phải là biến liên tục (dạng khoảng, tỉ lệ)
- Tính chất biến độc lập: Biến độc lập là biến danh mục (từ hai mức trở lên). Xem thêm các loại thang đo trong phân tích dữ liệu
- Tính độc lập: Các quan sát trong mỗi nhóm và giữa các nhóm độc lập với nhau
- Cỡ mẫu phù hợp: Mặc dù cỡ mẫu càng lớn thì càng tốt nhưng MANOVA một chiều đòi hỏi có nhiều quan sát trong mỗi nhóm hơn là số biến phụ thuộc
- Không có điểm dị biệt: Dữ liệu không có chứa các điểm dị biệt (Xem thêm phát hiện điểm dị biệt)
- Phân phối chuẩn: Dữ liệu của các biến phụ thuộc ở mỗi nhóm phải có dạng phân phối chuẩn hoặc xấp xỉ phân phối chuẩn (Xem thêm Phân phối chuẩn)
- Quan hệ tuyến tính: Có mối quan hệ tuyến tính giữa các biến phụ thuộc với biến độc lập trong mỗi nhóm của biến độc lập
- Tính đồng nhất: Tính đồng nhất trong ma trận hiệp phương sai
Thực hành phân tích MANOVA trên SPSS
Chuẩn bị dữ liệu: Đảm bảo bạn đã có bộ dữ liệu hsb.sav hoặc dữ liệu tương tự với cấu trúc gồm biến độc lập phân loại và ít nhất hai biến phụ thuộc liên tục.
Vào Analyze → General Linear Model → Multivariate…
Bước 2: Thiết lập biến
Cửa sổ Multivariate mở ra chúng ta chuyển:
- Biến độc lập prog vào khung Fixed Factor(s):
- Biến phụ thuộc science và socst vào khung Dependent Variables:
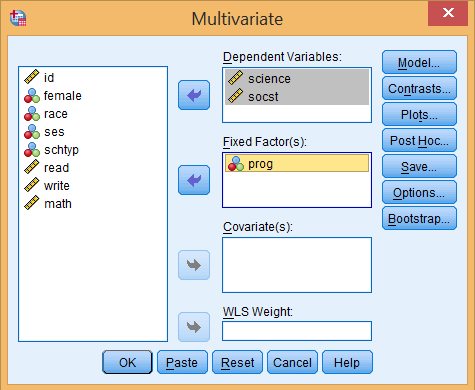
Bước 3: Thiết lập đồ thị
Bấm nút Plots… và thực hiện các bước sau:
- Chuyển biến prog vào khung Horizontal Axis:
- Bấm nút Add để đưa biến prog vào đồ thị
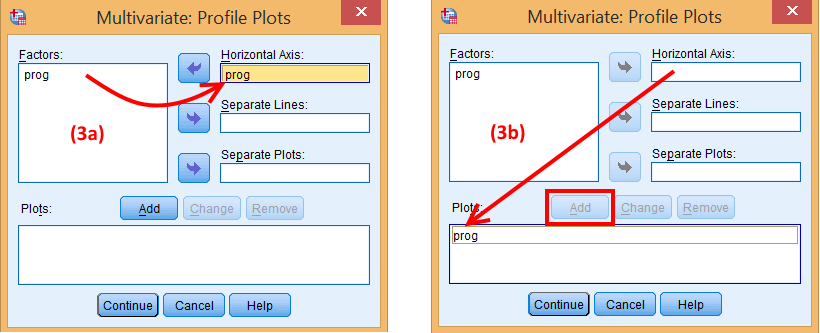
Bấm nút Continue để trở về cửa sổ Multivariate.
Bước 4: Thiết lập Post-Hoc
Bấm nút Post-Hoc… cửa sổ Multivariate: Post Hoc Multiple Comparisons for Observed… hiện ra:
- Đưa biến prog vào khung Post Hoc Tests for:
- Chọn kiểm định Tukey trong phần Equal Variances Assumed
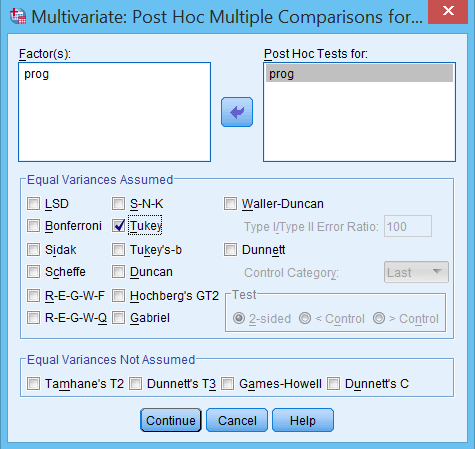
Lưu ý: Việc lựa chọn Post-Hoc là tùy thuộc vào dữ liệu và thiết kế nghiên cứu của bạn. Nếu biến độc lập của bạn chỉ có hai mức thì không cần phải thực hiện Post-Hoc này.
Bấm nút Continue để trở về cửa sổ Multivariate.
Bước 5: Thiết lập Options
Bấm nút Options… cửa sổ Multivariate: Options hiện ra:
- Chuyển biến prog từ khung Factor(s) and Factor Interactions: sang khung Display Means for
- Đánh dấu các tùy chọn: Descriptive statistics, Estimates of effect size, Observed power, và Homogeneity tests
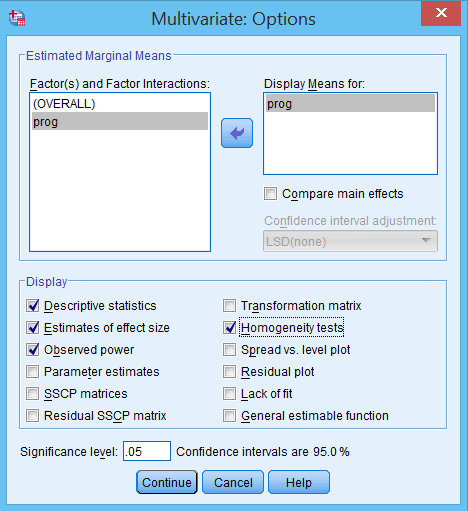
Bấm nút Continue để trở về cửa sổ Multivariate.
Bước 6: Thực hiện phân tích
Bấm nút OK để tiến hành phân tích.
Code tương đương trong các phần mềm khác
SPSS Syntax
* Phân tích MANOVA một chiều trong SPSS
* Kiểm tra sự khác biệt điểm môn khoa học và xã hội theo chương trình học
MANOVA science socst BY prog(1,3)
/PRINT=CELLINFO(MEANS) HOMOGENEITY(BOXM COCHRAN BARTLETT)
/PLOT=PROFILE(prog)
/POSTHOC=prog(TUKEY)
/DESIGN.
* Phân tích ANOVA riêng biệt cho từng biến phụ thuộc
ONEWAY science BY prog
/POSTHOC=TUKEY.
ONEWAY socst BY prog
/POSTHOC=TUKEY.
Hướng dẫn thực hành với R
# Tải thư viện cần thiết
library(car)
library(mvnormtest)
library(biotools)
# Đọc dữ liệu
data <- read.csv("hsb.csv")
# Tạo ma trận biến phụ thuộc
Y <- cbind(data$science, data$socst)
# Thực hiện MANOVA
manova_result <- manova(Y ~ prog, data = data)
# Xem kết quả tổng quát
summary(manova_result)
# Kiểm định Wilks' Lambda
summary(manova_result, test = "Wilks")
# Kiểm định Box's M test cho đồng nhất ma trận hiệp phương sai
boxM(Y, data$prog)
# Kiểm định Levene cho đồng nhất phương sai
leveneTest(science ~ prog, data = data)
leveneTest(socst ~ prog, data = data)
# Phân tích ANOVA từng biến
summary.aov(manova_result)
# Post-hoc test với Tukey
TukeyHSD(aov(science ~ prog, data = data))
TukeyHSD(aov(socst ~ prog, data = data))
Hướng dẫn thực hành với Python
import pandas as pd
import numpy as np
from scipy import stats
from statsmodels.multivariate.manova import MANOVA
from statsmodels.stats.contingency_tables import mcnemar
import matplotlib.pyplot as plt
import seaborn as sns
# Đọc dữ liệu
data = pd.read_csv('hsb.csv')
# Tạo DataFrame cho MANOVA
manova_data = data[['science', 'socst', 'prog']]
# Thực hiện MANOVA
manova = MANOVA.from_formula('science + socst ~ prog', data=manova_data)
result = manova.mv_test()
print("Kết quả MANOVA:")
print(result)
# Thống kê mô tả
desc_stats = data.groupby('prog')[['science', 'socst']].agg(['mean', 'std', 'count'])
print("\nThống kê mô tả:")
print(desc_stats)
# Vẽ biểu đồ box plot
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# Biểu đồ science
sns.boxplot(x='prog', y='science', data=data, ax=axes[0])
axes[0].set_title('Điểm môn khoa học theo chương trình')
axes[0].set_xlabel('Chương trình học')
axes[0].set_ylabel('Điểm số')
# Biểu đồ socst
sns.boxplot(x='prog', y='socst', data=data, ax=axes[1])
axes[1].set_title('Điểm môn xã hội theo chương trình')
axes[1].set_xlabel('Chương trình học')
axes[1].set_ylabel('Điểm số')
plt.tight_layout()
plt.show()
Hướng dẫn thực hành với Stata
* Đọc dữ liệu
use "hsb.dta", clear
* Mô tả dữ liệu theo nhóm
bysort prog: summarize science socst
* Thực hiện MANOVA
manova science socst = prog
* Kiểm định từng biến riêng lẻ
anova science prog
anova socst prog
* Post-hoc test với Tukey
pwcompare prog, effects mcompare(tukey)
* Kiểm tra giả thiết đồng nhất phương sai
robvar science, by(prog)
robvar socst, by(prog)
* Tạo biểu đồ so sánh
graph box science, over(prog) title("Điểm khoa học theo chương trình")
graph box socst, over(prog) title("Điểm xã hội theo chương trình")
Đọc kết quả phân tích MANOVA
Bảng Descriptive Statistics
Bảng Descriptive Statistics thể hiện các thông tin hữu ích về giá trị trung bình, độ lệch chuẩn cho hai biến phụ thuộc theo từng nhóm của biến độc lập. Kết quả thống kê mô tả các biến được hiển thị như sau:
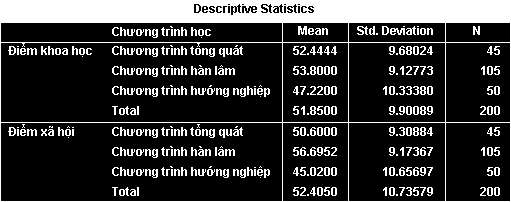
Cách đọc bảng: Từ bảng này, chúng ta có thể quan sát sự khác biệt ban đầu về điểm trung bình giữa các nhóm chương trình học cho cả hai môn khoa học và xã hội.
Kiểm tra các giả định
Box’s Test of Equality of Covariance Matrices
Bảng Box’s Test of Equality of Covariance Matrices với giả thuyết H₀ cho rằng ma trận hiệp phương sai của các biến phụ thuộc bằng nhau giữa các nhóm:

Với mức ý nghĩa Sig bằng 0.644 cho thấy chưa thể bác bỏ giả thuyết này (p > 0.05). Do vậy, ma trận hiệp phương sai thỏa mãn tính chất đồng nhất.
Diễn giải:- p > 0.05: Không vi phạm giả định đồng nhất ma trận hiệp phương sai
- p ≤ 0.05: Vi phạm giả định, cần thận trọng khi diễn giải kết quả
Levene’s Test of Equality of Error Variances
Bảng Levene’s Test of Equality of Error Variances với giả thuyết H₀ cho rằng phương sai của sai số ở mỗi biến phụ thuộc bằng nhau giữa các nhóm:

Mức ý nghĩa của kiểm định Levene cho hai biến science và socst lần lượt là 0.628 và 0.288 đều không có ý nghĩa thống kê ở mức 5%. Điều đó cho thấy, phương sai của sai số ở hai biến phụ thuộc không đổi giữa các nhóm.
Bảng Multivariate Tests – Kết quả chính
Bảng Multivariate Tests sẽ trả lời cho câu hỏi đặt ra đầu bài theo phương pháp phân tích MANOVA một chiều:

Sự khác nhau về điểm số môn học giữa các nhóm chương trình học được thể hiện ở dòng thứ hai (prog). Chúng ta quan tâm đến dòng Wilks’ Lambda (đánh dấu màu đỏ).
Với kết quả trên, mức ý nghĩa thống kê theo kiểm định Wilks’ Lambda bằng 0.000 (nhỏ hơn mức ý nghĩa 5%). Vì vậy, chúng ta có thể kết luận có sự khác nhau về năng lực học được thể hiện qua điểm của hai môn học (science và socst) theo các chương trình học.
Kết luận: Có bằng chứng thống kê để khẳng định rằng các chương trình học khác nhau có tác động khác nhau đến kết quả học tập của sinh viên (xét trên cả hai môn khoa học và xã hội).
Hiểu về các loại kiểm định trong MANOVA
- Pillai’s Trace: Bền vững nhất khi vi phạm giả định
- Wilks’ Lambda: Phổ biến nhất, cân bằng giữa sức mạnh và tính bền vững
- Hotelling’s Trace: Mạnh nhất khi thỏa mãn đầy đủ giả định
- Roy’s Largest Root: Nhạy cảm nhất, chỉ sử dụng khi chắc chắn về giả định
Bảng Tests of Between-Subjects Effects
Để xác định giá trị các biến phụ thuộc khác nhau như thế nào theo các nhóm của biến độc lập, chúng ta sử dụng bảng Tests of Between-Subjects Effects:
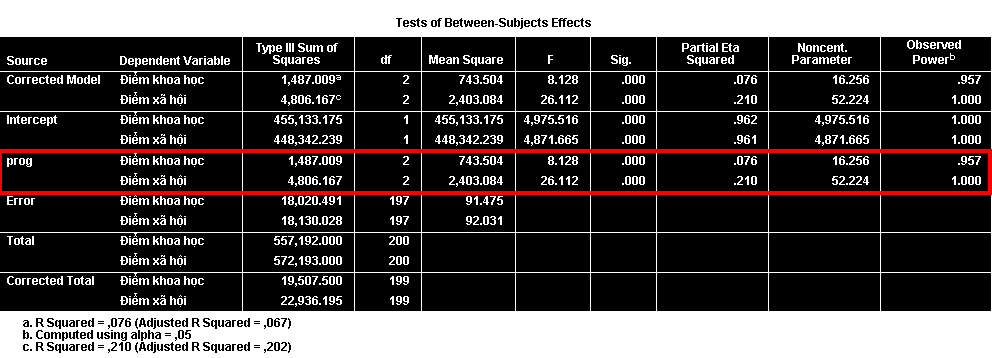
Chúng ta quan tâm đến mức ý nghĩa của dòng prog (được tô viền đỏ). Kết quả cho thấy kết quả của hai môn học đều khác nhau theo các chương trình học với mức ý nghĩa thống kê.
Kết quả phân tích Post-Hoc
Để hiểu rõ hơn về sự khác nhau về điểm số các môn học theo ba chương trình học khác nhau, chúng ta sử dụng kết quả phân tích Post-Hoc. Kết quả phân tích Post-Hoc kiểm định Tukey được trình bày ở bảng Multiple Comparisons:
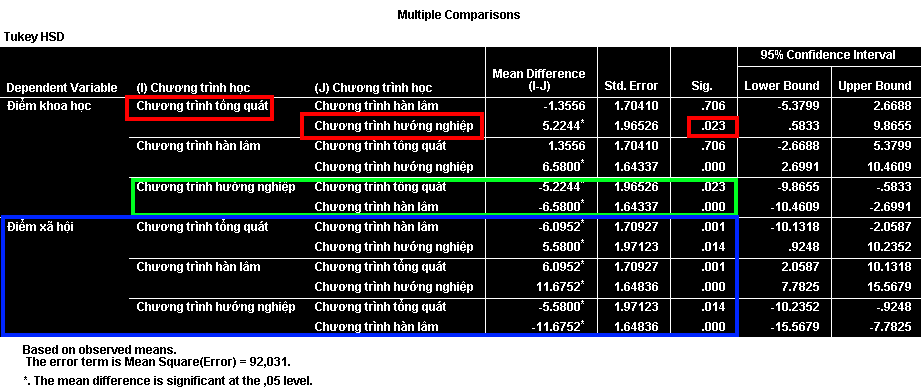
Phân tích điểm môn Khoa học
Theo kết quả, điểm số môn khoa học của những sinh viên theo chương trình tổng quát cao hơn 5.224 điểm so với những sinh viên theo học chương trình hướng nghiệp với mức ý nghĩa 5% (Sig = 0.023). Điều này cũng tương tự đối với những sinh viên theo học chương trình hàn lâm (cao hơn 6.58 điểm, mức ý nghĩa Sig = 0.000).
Tuy nhiên, không có sự chênh lệch có ý nghĩa thống kê về điểm khoa học giữa những sinh viên theo học chương trình hàn lâm và chương trình tổng quát.
Phân tích điểm môn Xã hội
Tương tự điểm số môn khoa học, điểm số môn xã hội của những sinh viên theo học chương trình hướng nghiệp đều thấp hơn so với hai chương trình còn lại (mức ý nghĩa 5%). Tuy nhiên có sự khác nhau giữa điểm số môn xã hội ở những sinh viên theo học chương trình tổng quát và hàn lâm. Cụ thể là những sinh viên theo học chương trình hàn lâm sẽ có điểm xã hội cao hơn những sinh viên theo học chương trình tổng quát là 6.095 điểm (Sig = 0.001).
Đồ thị Estimated Marginal Means
Đồ thị Estimated Marginal Means đánh giá tác động biên về sự chênh lệch điểm số của một sinh viên theo một chương trình học này so với hai chương trình học còn lại. Đồ thị này thể hiện trực quan sự khác nhau về điểm số giữa các chương trình ở hai môn học đã lần lượt trình bày ở bảng Descriptive Statistics hoặc bảng Multiple Comparisons trong phân tích Post-Hoc ở trên.
Lưu ý quan trọng và khuyến nghị
Các điều cần lưu ý:
- MANOVA nhạy cảm với việc vi phạm giả định phân phối chuẩn đa biến
- Cần cỡ mẫu lớn hơn đáng kể so với ANOVA đơn biến
- Khi có nhiều biến phụ thuộc, việc giải thích kết quả trở nên phức tạp
- Cần kiểm tra vấn đề đa cộng tuyến giữa các biến phụ thuộc
Khi nào nên sử dụng MANOVA
- Khi có từ hai biến phụ thuộc liên tục trở lên có mối quan hệ lý thuyết
- Muốn kiểm soát lỗi Type I khi thực hiện nhiều so sánh
- Các biến phụ thuộc có tương quan với nhau (nhưng không quá cao)
- Cỡ mẫu đủ lớn (ít nhất 20 quan sát/biến phụ thuộc trong mỗi nhóm)
Các phương pháp thay thế
Nếu không thỏa mãn giả định MANOVA, có thể xem xét:
- Separate ANOVA: Thực hiện ANOVA riêng biệt với điều chỉnh Bonferroni
- Permutation MANOVA: Khi vi phạm giả định phân phối chuẩn
- Robust MANOVA: Khi có điểm dị biệt hoặc vi phạm giả định
- Non-parametric MANOVA: Cho dữ liệu không chuẩn
Ứng dụng thực tế trong nghiên cứu kinh tế Việt Nam
Trường hợp nghiên cứu 1: Đánh giá chính sách giáo dục
Một nghiên cứu được thực hiện tại 30 trường THPT ở các tỉnh miền Bắc để đánh giá hiệu quả của ba mô hình giảng dạy khác nhau (truyền thống, STEM, và tích hợp công nghệ) đối với kết quả học tập của học sinh lớp 12.
Thiết kế nghiên cứu:
- Biến độc lập: Mô hình giảng dạy (ba nhóm)
- Biến phụ thuộc: Điểm thi THPT Quốc gia môn Toán, Lý, Hóa
- Cỡ mẫu: 450 học sinh (150 học sinh/nhóm)
Trường hợp nghiên cứu 2: Nghiên cứu thị trường lao động
Phân tích tác động của trình độ học vấn (THCS, THPT, Đại học) đến các chỉ số việc làm của lao động trẻ tại TP.HCM.
Thiết kế nghiên cứu:
- Biến độc lập: Trình độ học vấn (ba nhóm)
- Biến phụ thuộc: Mức lương, mức độ hài lòng công việc, cơ hội thăng tiến
- Cỡ mẫu: 600 lao động trẻ (200 người/nhóm)
Trường hợp nghiên cứu 3: Đánh giá hiệu quả đào tạo doanh nghiệp
Một tập đoàn lớn tại Việt Nam muốn đánh giá hiệu quả của ba chương trình đào tạo nhân viên khác nhau (online, offline, blended learning) đối với năng lực làm việc.
Thiết kế nghiên cứu:
- Biến độc lập: Hình thức đào tạo (ba nhóm)
- Biến phụ thuộc: Điểm đánh giá kỹ năng chuyên môn, kỹ năng mềm, hiệu suất công việc
- Cỡ mẫu: 300 nhân viên (100 người/nhóm)
Tổng kết
MANOVA một chiều là công cụ thống kê mạnh mẽ và linh hoạt trong thực hành kinh tế lượng, đặc biệt hữu ích khi cần đánh giá tác động của một yếu tố lên nhiều biến kết quả cùng lúc. Phương pháp này không chỉ giúp kiểm soát lỗi Type I mà còn cung cấp cái nhìn tổng thể về mối quan hệ giữa các biến.Tuy nhiên, để sử dụng MANOVA hiệu quả, người phân tích cần:
- Hiểu rõ về lý thuyết và giả định của phương pháp
- Kiểm tra kỹ lưỡng các điều kiện áp dụng
- Diễn giải kết quả một cách thận trọng và có căn cứ
- Kết hợp với các phương pháp phân tích khác để có cái nhìn hoàn chỉnh
Trong bối cảnh nghiên cứu kinh tế và xã hội tại Việt Nam, MANOVA đặc biệt phù hợp cho các nghiên cứu đánh giá chính sách, hiệu quả chương trình, và so sánh nhóm đối tượng với nhiều tiêu chí kết quả.
Điểm quan trọng cần nhớ:
- MANOVA mở rộng khả năng phân tích từ một biến phụ thuộc sang nhiều biến cùng lúc
- Wilks’ Lambda là thống kê được sử dụng phổ biến nhất do tính cân bằng
- Cần kiểm tra đầy đủ các giả định trước khi thực hiện phân tích
- Phân tích post-hoc là bước cần thiết để hiểu rõ sự khác biệt giữa các nhóm
- Kết hợp nhiều phần mềm thống kê giúp tăng độ tin cậy và tính toàn diện của phân tích